Содержание
- 2. Открытие логарифма Определение логарифма Свойства логарифмов Дополнительные формулы Свойства логарифмической функции График функции Решение логарифмических уравнений
- 3. История логарифма началась в 17 веке. Логарифмы были изобретены шотландским дворянином Джоном Непером (1550-1617),опубликовавшим свои работы
- 4. Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести a, чтобы получить
- 5. Свойства логарифмов При любом a > 0 (a = 1) и любых положительных x и y:
- 6. loga b = logn b*logm c=logm b*logn c logak bk = loga b Дополнительные формулы
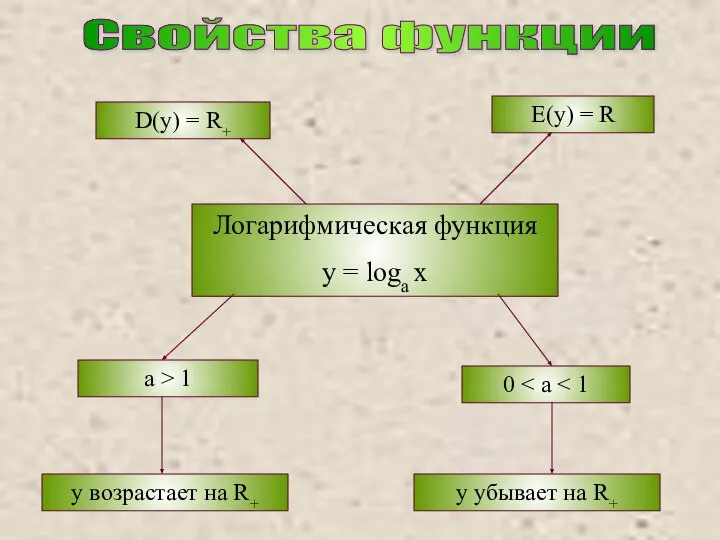
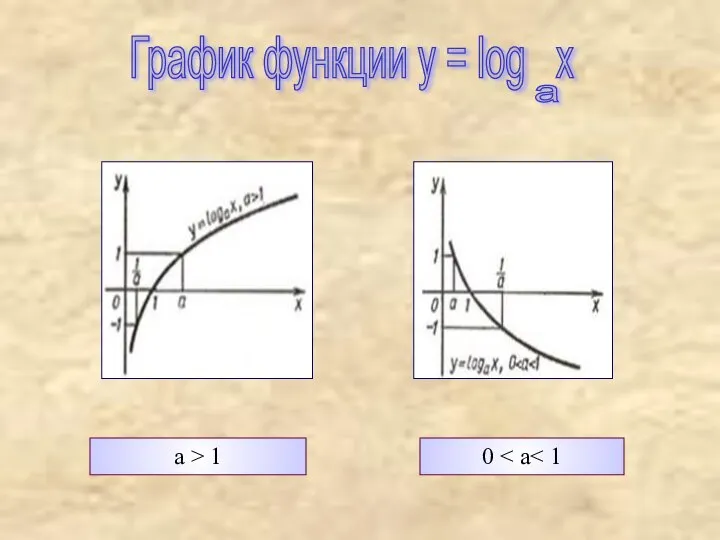
- 7. Логарифмическая функция y = loga x D(y) = R+ E(y) = R a > 1 0
- 8. a > 1 0
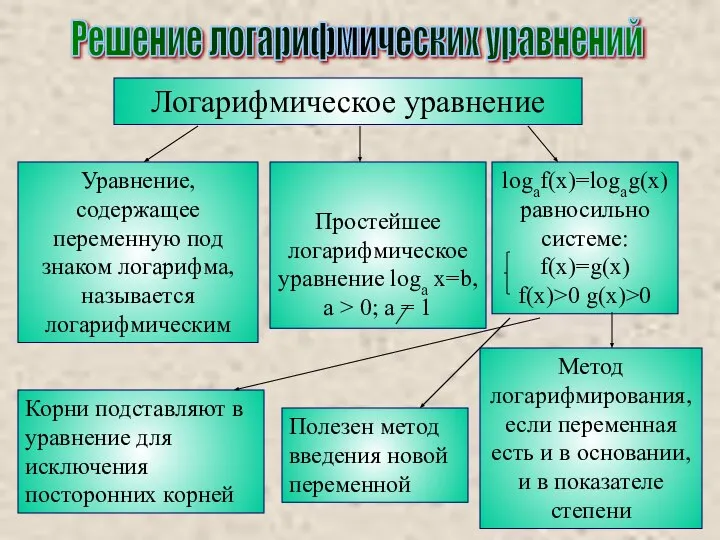
- 9. Решение логарифмических уравнений Логарифмическое уравнение Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим Простейшее логарифмическое уравнение
- 10. Примеры решения уравнений xlog2x+2=8 Прологарифмируем обе части уравнения по основанию 2: log2(xlog2x+2)=log28, (log2x+2)*log2x=3. Пусть log2x=y, тогда
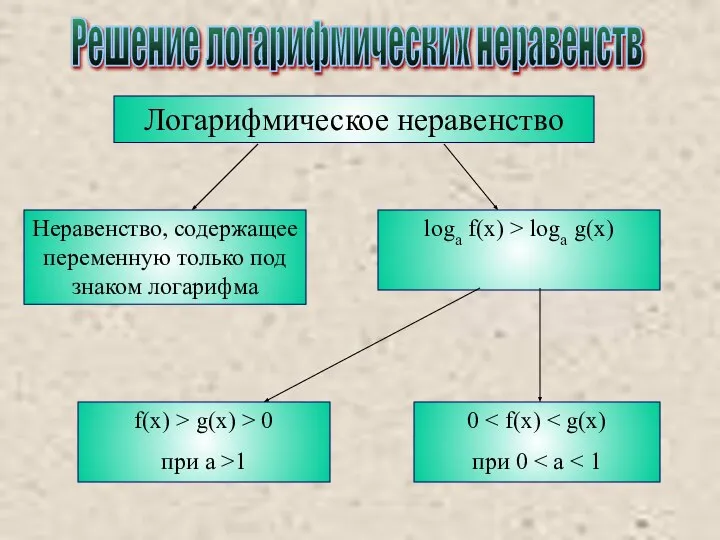
- 11. Решение логарифмических неравенств Логарифмическое неравенство Неравенство, содержащее переменную только под знаком логарифма loga f(x) > loga
- 12. Примеры решения неравенств log5 (x - 3) x – 3 > 0 x – 3 x
- 14. Скачать презентацию







 Есептеу әдістемесі мен механикалық құралжабдықтарды таңдау
Есептеу әдістемесі мен механикалық құралжабдықтарды таңдау Лидерство и стили менеджмента
Лидерство и стили менеджмента Клифф (Хай)- Дайвинг
Клифф (Хай)- Дайвинг Платформа Ардуино
Платформа Ардуино Урок учителя истории Родновой Елены Юрьевны. - презентация
Урок учителя истории Родновой Елены Юрьевны. - презентация Дифракция света
Дифракция света  Аттестационная работа. Метод проектов, как способ преподавания теоретической части предмета физическая культура
Аттестационная работа. Метод проектов, как способ преподавания теоретической части предмета физическая культура Национальные интересы РФ, стратегия в направлениях: сфера деятельности, социальная, военная, информационная и политическая
Национальные интересы РФ, стратегия в направлениях: сфера деятельности, социальная, военная, информационная и политическая Научно-техническая революция в 50е-60е годы XX века Презентацию подготовил студент первого курса ФТД-111 Бобырь Алексей
Научно-техническая революция в 50е-60е годы XX века Презентацию подготовил студент первого курса ФТД-111 Бобырь Алексей Способы включения трехфазных двигателей в однофазную сеть
Способы включения трехфазных двигателей в однофазную сеть Единая система конструкторской дисциплины
Единая система конструкторской дисциплины Мастера Гжели
Мастера Гжели ЛЭПБУК по УМК (учебно-методическому комплекту) по изучению национального языка
ЛЭПБУК по УМК (учебно-методическому комплекту) по изучению национального языка Типы лидеров
Типы лидеров Когато чуеш думата бетон......
Когато чуеш думата бетон...... Нелинейные явления в радиотракте. Перекрестная модуляция и ее оценка. Взаимная модуляция и ее оценка
Нелинейные явления в радиотракте. Перекрестная модуляция и ее оценка. Взаимная модуляция и ее оценка ТЕРРОРИЗМ
ТЕРРОРИЗМ Сельское хозяйство в России
Сельское хозяйство в России Интернационализация и ее воздействие на стратегию нового университета Джон Филден
Интернационализация и ее воздействие на стратегию нового университета Джон Филден Сью Таунсенд
Сью Таунсенд Солтүстік Америкадағы этностар мен халықтар. Мәдениеті
Солтүстік Америкадағы этностар мен халықтар. Мәдениеті Cпектры некоторых неинтегрируемыхфункций
Cпектры некоторых неинтегрируемыхфункций Основные аспекты и тенденции риск-менеджмента
Основные аспекты и тенденции риск-менеджмента Интеллектуальная разминка по теме: «Формы государства в зарубежных странах»
Интеллектуальная разминка по теме: «Формы государства в зарубежных странах» Электротехнологии часть 1
Электротехнологии часть 1 РОССИЙСКИЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ КОНЦЕРН «РУСЭЛПРОМ» Объединение предприятий по производству электротехнического оборудования и
РОССИЙСКИЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ КОНЦЕРН «РУСЭЛПРОМ» Объединение предприятий по производству электротехнического оборудования и  Средства измерений их классификация
Средства измерений их классификация  Русский быт 18 века
Русский быт 18 века