Презентация Модель множественной линейной регрессии Вопросы 1. Задача построения множественной линейной регрессии. 2. Оценка кач
Содержание
- 2. 1. В общем случае зависимая переменная у может быть функцией нескольких переменных: х1, х2, …, хm.
- 3. Введем матричные обозначения. Пусть {αj}, j = 1,…, m – вектор неизвестных параметров; Y = {yi},
- 4. Относительно ошибок ε сделаем следующие предположения: 1) возмущение ε является случайной величиной; 2) М(ε) = 0;
- 5. Последнее обстоятельство эквивалентно тому, что ранг матрицы Х равен m, а это, в свою очередь, означает,
- 6. Оценку выражения (1), полученную по выборочным данным, запишем в виде yi = a1xi1 + a2xi2 +
- 7. Продифференцируем Q по а, получим Оценку а, найденную по формуле (5), будем называть оценкой МНК.
- 8. Таким образом, для определения вектора а необходимо по данным наблюдений найти матрицу, обратную к матрице Х′X,
- 10. Обычно предполагается, что уравнение регрессии имеет свободный член, т.е. а0. Чтобы получить оценку этого параметра, расширим
- 11. Тогда матрицу Х в развернутом виде можно записать так:
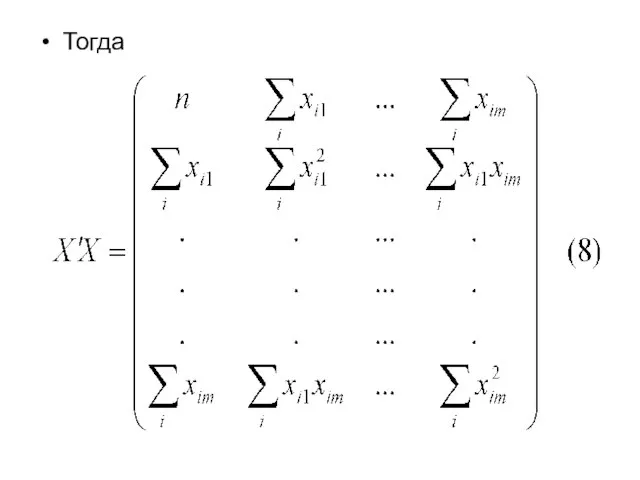
- 12. Тогда
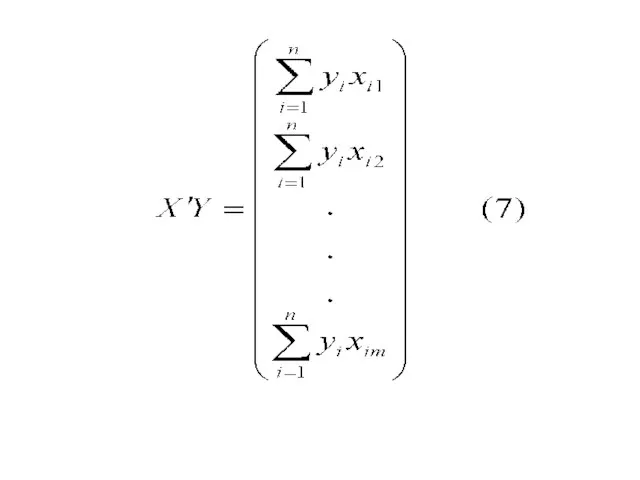
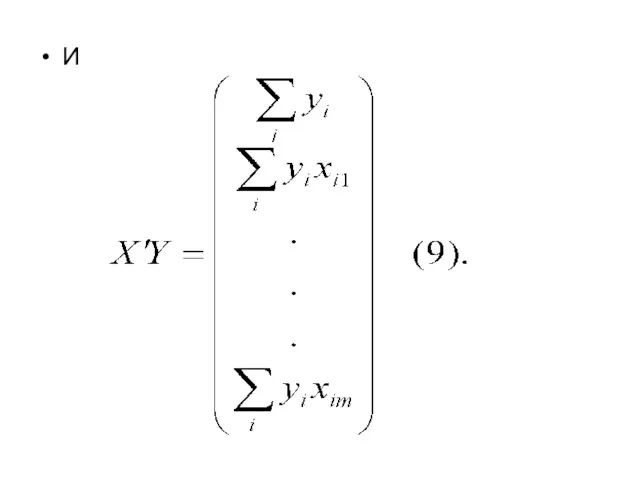
- 13. И
- 14. В частном случае, когда m=2, имеем
- 15. Условный пример
- 16. Таким образом,
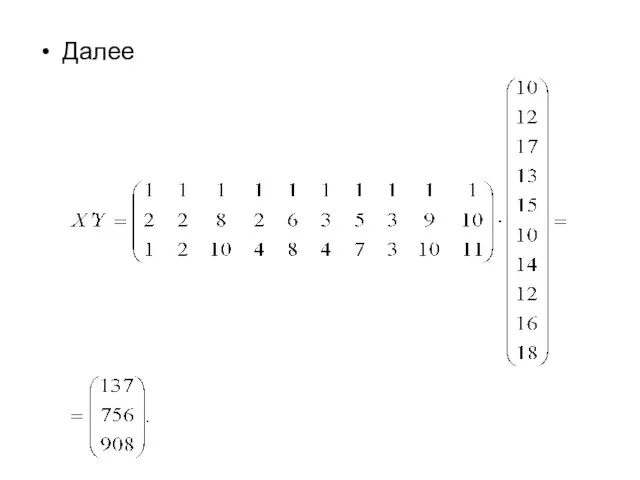
- 18. Далее
- 19. Замечание Матрицу X′X и вектор X′Y можно получить и по формулам (8) и (9), предварительно подсчитав
- 20. Определив X′X и X′Y, находим а: а = (X′X)-1X′Y = Таким образом, искомое уравнение
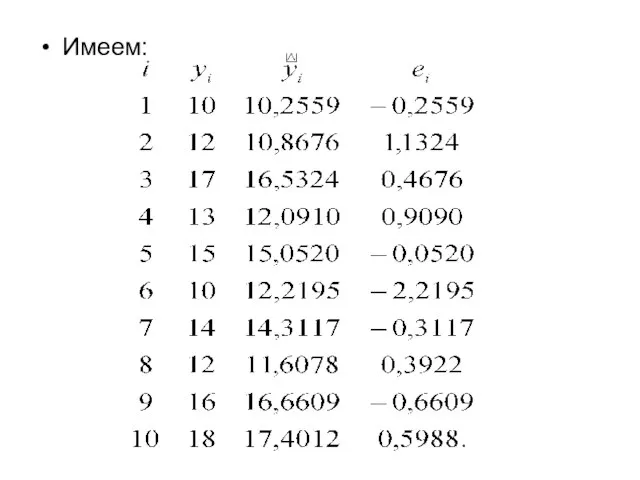
- 21. Приведем рассчитанные по данному уравнению регрессии значения независимой переменной (уi) и соответствующие ошибки (еi):
- 22. Имеем:
- 24. Скачать презентацию
















 Gospodarowanie zasobami materialnymi w organizacji
Gospodarowanie zasobami materialnymi w organizacji Презентация «ГРАЖДАНЕ (ФИЗИЧЕСКИЕ ЛИЦА) КАК СУБЪЕКТЫ ГРАЖДАНСКОГО ПРАВА»
Презентация «ГРАЖДАНЕ (ФИЗИЧЕСКИЕ ЛИЦА) КАК СУБЪЕКТЫ ГРАЖДАНСКОГО ПРАВА» Цели и принципы кредитно-денежной политики Подготовила студентка ФТД-4 группы Т-103 Лепичева Наталия
Цели и принципы кредитно-денежной политики Подготовила студентка ФТД-4 группы Т-103 Лепичева Наталия Уплотнения опор
Уплотнения опор Внешнеэкономическое информирование Подготовила: Белоглазова Ю.В., группа ДС-01 МЭ-101
Внешнеэкономическое информирование Подготовила: Белоглазова Ю.В., группа ДС-01 МЭ-101 Красный крест
Красный крест  ВЕКСЕЛЬ И ВЕКСЕЛЬНОЕ ОБРАЩЕНИЕ Функции и виды векселей Общая характеристика векселя как ценной бумаги Понятия, используемые
ВЕКСЕЛЬ И ВЕКСЕЛЬНОЕ ОБРАЩЕНИЕ Функции и виды векселей Общая характеристика векселя как ценной бумаги Понятия, используемые  Презентация ВИДЫ И ОБРАБОТКА КОЖИ
Презентация ВИДЫ И ОБРАБОТКА КОЖИ Средние века и Возрождение
Средние века и Возрождение  Электронный репетитор
Электронный репетитор Классификация уровней менеджеров. Функции, выполняемые менеджерами
Классификация уровней менеджеров. Функции, выполняемые менеджерами Дидактические игры на уроках - презентация для начальной школы_
Дидактические игры на уроках - презентация для начальной школы_ Нахождение характеристик рассеянной волны
Нахождение характеристик рассеянной волны Использование комплексов подводящих упражнений в подготовке детей, занимающихся футболом
Использование комплексов подводящих упражнений в подготовке детей, занимающихся футболом организация амбулаторно-поликлинической помощи населению
организация амбулаторно-поликлинической помощи населению АСПИРАЦИОННОЕ УПРАВЛЕНИЕ (ASPIRATIONAL MANAGEMENT)
АСПИРАЦИОННОЕ УПРАВЛЕНИЕ (ASPIRATIONAL MANAGEMENT) Клининико - анатомическое, гистологическое строение пульпы зуба
Клининико - анатомическое, гистологическое строение пульпы зуба  Саморасстановки. Эффективный метод саморазвития
Саморасстановки. Эффективный метод саморазвития Тип подшипника. Схема установки подшипника на вал
Тип подшипника. Схема установки подшипника на вал Презентация "К. Ф. Юон" - скачать презентации по МХК
Презентация "К. Ф. Юон" - скачать презентации по МХК Автор: Семко Светлана Анатольевна, учитель русского языка, литературы и МХК
Автор: Семко Светлана Анатольевна, учитель русского языка, литературы и МХК  Блиц-турнир Повторение и систематизация материала по теме «Чрезвычайные ситуации на транспорте»
Блиц-турнир Повторение и систематизация материала по теме «Чрезвычайные ситуации на транспорте» Мультимедийные технологии обработки информации
Мультимедийные технологии обработки информации Christmas in Germanу
Christmas in Germanу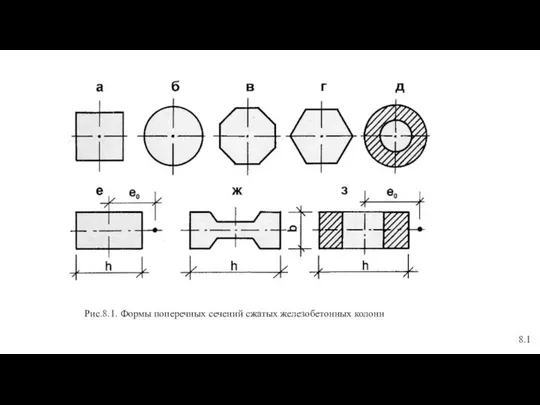 Формы поперечных сечений сжатых железобетонных колонн
Формы поперечных сечений сжатых железобетонных колонн Критические периоды постнатального онтогенеза
Критические периоды постнатального онтогенеза  Презентация "Государственно-частное партнёрство" - скачать презентации по Экономике
Презентация "Государственно-частное партнёрство" - скачать презентации по Экономике МОЛЕКУЛЯРНАЯ ГЕНЕТИКА
МОЛЕКУЛЯРНАЯ ГЕНЕТИКА