Содержание
- 2. /23 Литература Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В. Федосеева.
- 3. Известные ученые-экономисты Леонид Витальевич Канторович родился 19 января 1912г. в Санкт-Петербурге в семье врача. В 18
- 4. /23 3.1. Принцип оптимальности в планировании и управлении Принцип оптимальности предполагает следующее: наличие определённых ресурсов наличие
- 5. Задачи линейного программирования Возможные области применения задач ЛП: рациональное использование сырья и материалов; задачи составления смесей;
- 6. /23 3.2. Задача линейного программирования Это развёрнутая форма записи Линейная целевая функция Линейные ограни-чения Условия неотрицательности
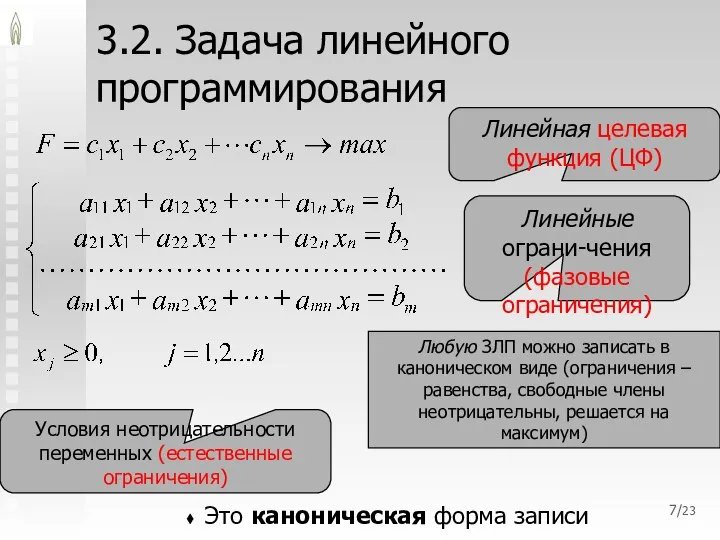
- 7. /23 3.2. Задача линейного программирования Это каноническая форма записи Линейная целевая функция (ЦФ) Линейные ограни-чения (фазовые
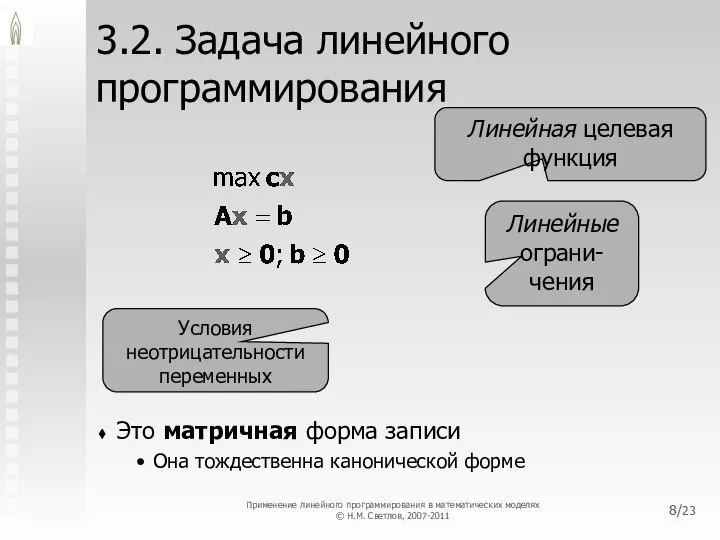
- 8. /23 3.2. Задача линейного программирования Это матричная форма записи Она тождественна канонической форме Линейная целевая функция
- 9. /23 3.2. Задача линейного программирования Это стандартная форма записи Линейная целевая функция Линейные ограни-чения Условия неотрицательности
- 10. /23 3.2. Любой вектор x, удовлетворяющий ограничениям и условиям неотрицательности (безотносительно к целевой функции), называется допустимым
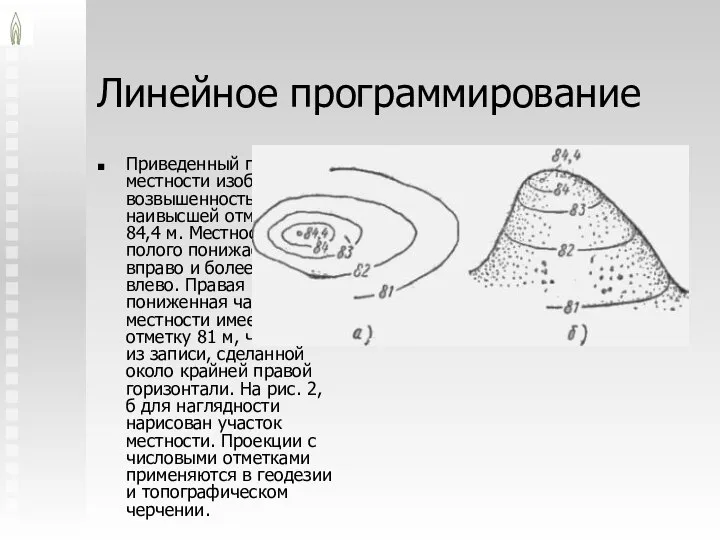
- 11. Линейное программирование Приведенный план местности изображает возвышенность с наивысшей отметкой 84,4 м. Местность полого понижается вправо
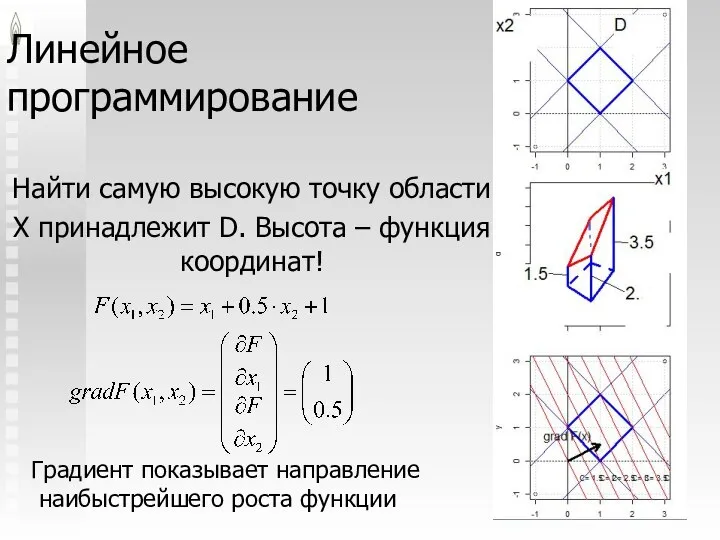
- 12. Линейное программирование Найти самую высокую точку области X принадлежит D. Высота – функция координат! Градиент показывает
- 13. /23 3.2. ЗЛП может: не иметь ни одного оптимального решения допустимой области не существует – система
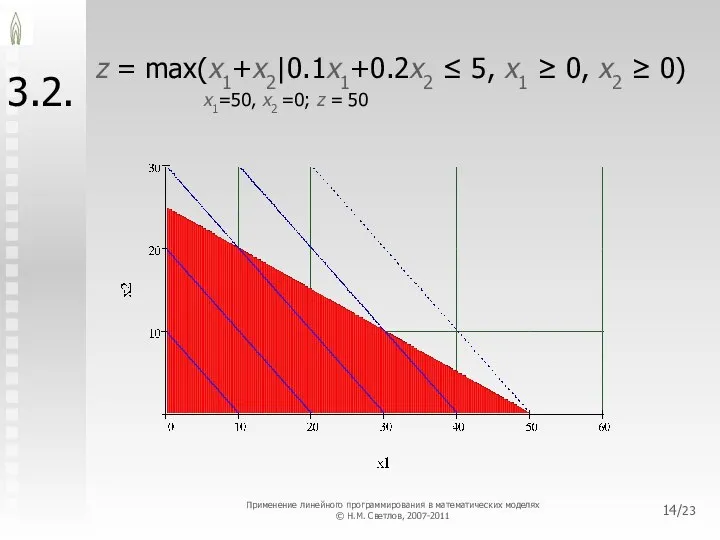
- 14. /23 3.2. z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1 ≥ 0, x2 ≥ 0) x1=50, x2 =0;
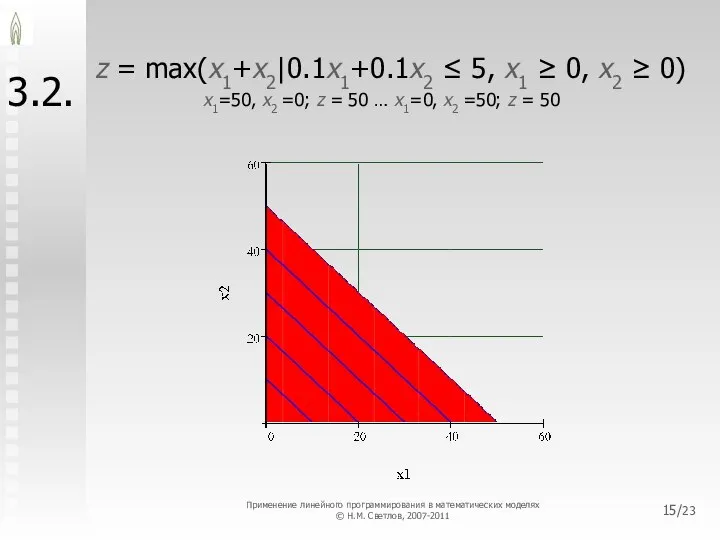
- 15. /23 3.2. z = max(x1+x2|0.1x1+0.1x2 ≤ 5, x1 ≥ 0, x2 ≥ 0) x1=50, x2 =0;
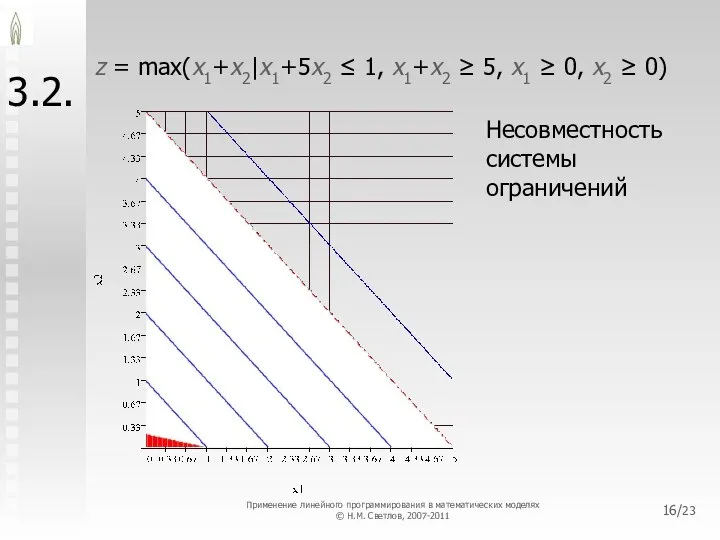
- 16. /23 3.2. z = max(x1+x2|x1+5x2 ≤ 1, x1+x2 ≥ 5, x1 ≥ 0, x2 ≥ 0)
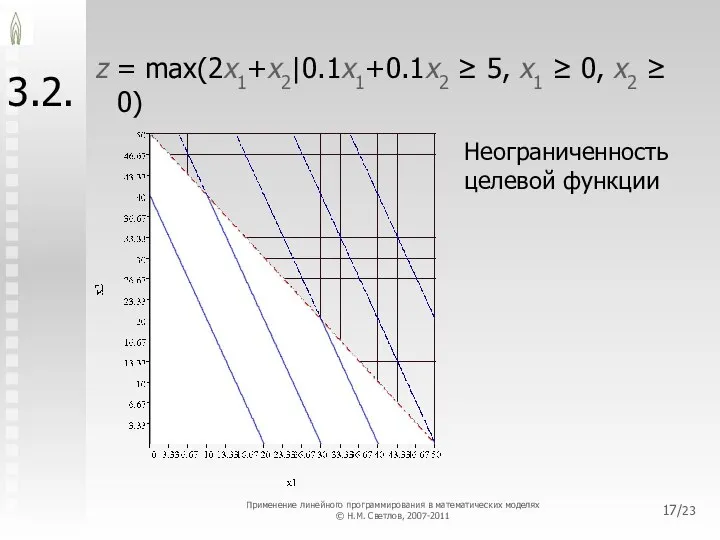
- 17. /23 3.2. z = max(2x1+x2|0.1x1+0.1x2 ≥ 5, x1 ≥ 0, x2 ≥ 0) Неограниченность целевой функции
- 18. Геометрический смысл задачи линейного программирования
- 19. Задача о диете Составить задачу ЛП, позволяющую оптимизировать расход кормов, и привести ее к каноническому виду.
- 20. Задача о диете Задача ЛП Задача ЛП в канонической форме!
- 21. Задача о диете В 1982 г. Джорджу Стиглеру была присуждена Нобелевская премия за труды по теории
- 22. Задача о диете=Задача о смеси Найти самую дешевую допустимую смесь.
- 23. /23 3.3. Симплексный метод Ограничения ЗЛП в канонической форме приводятся к виду Переменные (неизвестные) называются базисными,
- 24. /23 3.3. Симплексный метод Подставляя в ЦФ вместо базисных переменных их выражения через свободные переменные из
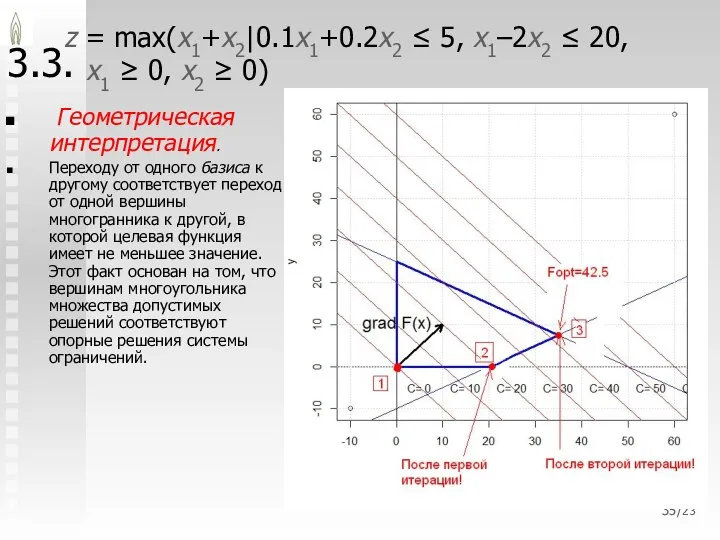
- 25. /23 3.3. Симплексный метод Геометрическая интерпретация. Аналитическому переходу от одного базиса к другому соответствует переход от
- 26. /23 3.3. Симплексный метод Исходные условия применения симплексного метода ЗЛП записана в канонической форме Её ограничения
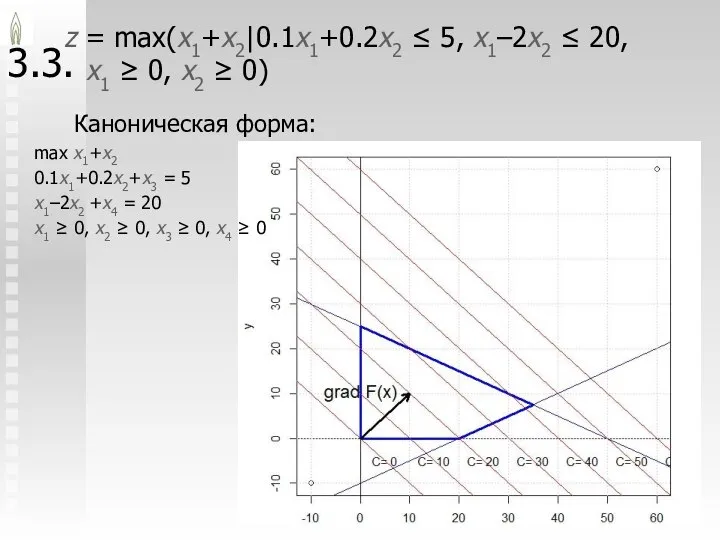
- 27. /23 3.3. z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1–2x2 ≤ 20, x1 ≥ 0, x2 ≥ 0)
- 28. Теория принятия решений ПетрГУ, А.П.Мощевикин, 2004 г. Симплекс-метод ЛП Запись задачи в виде уравнений x1 +
- 29. /23 3.3. z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1–2x2 ≤ 20, x1 ≥ 0, x2 ≥ 0)
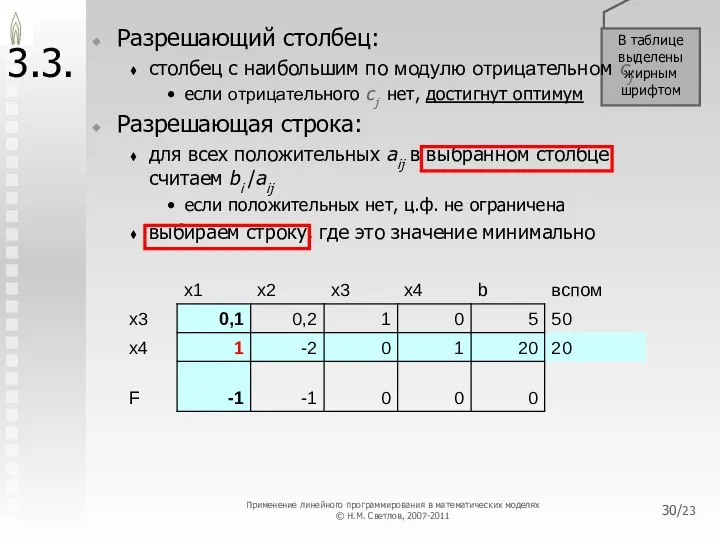
- 30. /23 В таблице выделены жирным шрифтом 3.3. Разрешающий столбец: столбец с наибольшим по модулю отрицательном cj
- 31. /23 3.3. Выполняем обыкновенные жордановы исключения во всей таблице: для строк i ≠i' : aijнов =
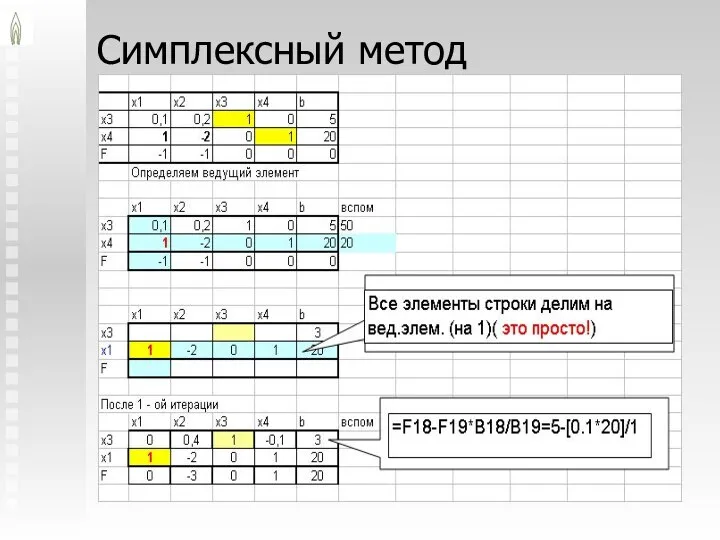
- 32. Симплексный метод
- 33. Каноническая форма: max 20+3x2-x4 x3 = 3 -0.4x1+0.1x4 x1= 20 +2x2 -x4 x1 ≥ 0, x2
- 34. Отрицательных cj больше нет – достигнут оптимум (в больших задачах для этого требуются тысячи итераций) Каноническая
- 35. /23 3.3. z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1–2x2 ≤ 20, x1 ≥ 0, x2 ≥ 0)
- 36. /23 3.3. Симплексный метод Исходные условия применения симплексного метода ЗЛП записана в канонической форме Её ограничения
- 37. /23 3.3. Симплексный метод Вывод: Не всякая задача ЛП может быть решена непосредственным применением симплекс-метода. Для
- 38. /23 3.3. Симплексный метод Определение: Говорят, что ограничение задачи ЛП, имеет предпочтительный вид, если при неотрицательной
- 39. /23 3.3. 1. случай: система ограничений имеет вид Применение линейного программирования в математических моделях © Н.М.
- 40. /23 3.3. 2. случай: система ограничений имеет вид (напр. Задача о диете) Применение линейного программирования в
- 41. /23 3.3. метод искусственного базиса вводится искусственный базис: 1. К левым частям ограничений-равенств, не имеющих предпочтительного
- 42. /23 3.3. Метод искусственного базиса , . Теорема 2. Если в оптимальном плане М-задачи хотя бы
- 43. /23 3.3. Метод искусственного базиса Продолжение примера 1. Решение задачи о диете , . , М-задача
- 44. 3.3. Метод искусственного базиса , . , М-задача Применяем симплекс-метод, взяв в качестве базисных переменных искусственные
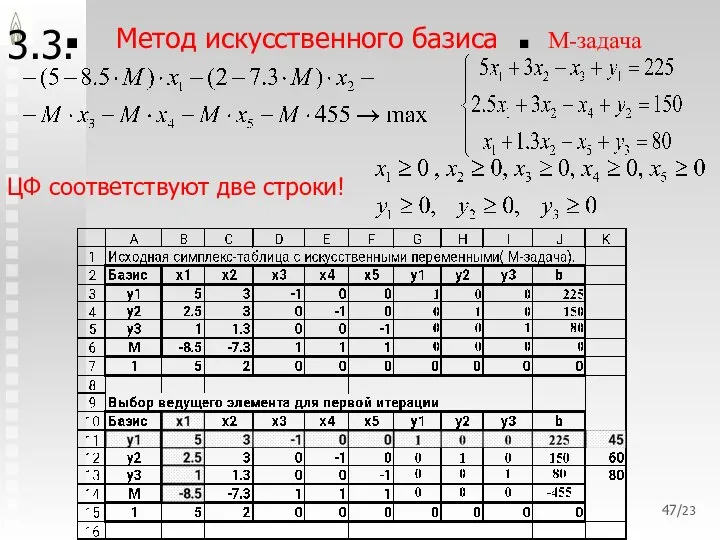
- 45. /23 3.3. Метод искусственного базиса , . , М-задача ЦФ соответствуют две строки! Коэффициенты в ЦФ
- 46. /23 3.3. Метод искусственного базиса , . , М-задача ход решения М-задачи: с ▲сначала избавляемся от
- 47. /23 3.3. Метод искусственного базиса , . , М-задача ЦФ соответствуют две строки!
- 48. /23 3.3. Метод искусственного базиса , . , М-задача
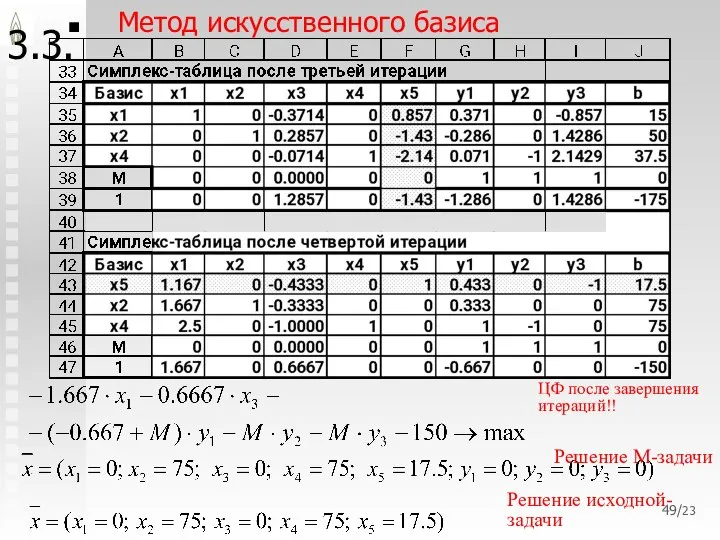
- 49. /23 3.3. Метод искусственного базиса , . , Решение М-задачи Решение исходной-задачи ЦФ после завершения итераций!!
- 50. /23 3.3. В некоторых случаях алгоритм симплексного метода может зацикливаться. Пути преодоления этой проблемы описаны в
- 51. ЗАДАЧА ОБ ОПТИМАЛЬНОМ РАСПРЕДЕЛЕНИИ РЕСУРСОВ Здесь (2.1) - целевая функция (ЦФ); (2.2) - система ограничений; (2.3)
- 52. Двойственная задача Правила: Каждому i-му ограничению исходной задачи соответствует переменная двойственной задачи ui (двойственная переменная). Каждой
- 53. Двойственная задача Правила: 1. Каждому i-му ограничению исходной задачи соответствует переменная двойственной задачи ui (двойственная переменная).
- 54. Двойственная задача Теорема 1 Пусть xj, j = 1, 2,…, n обозначает допустимый план прямой задачи,
- 55. Свойства решений (следствия из теорем двойственности!) Значения целевых функций для оптимальных решений прямой и двойственной задач
- 56. /23 3.4. Экономические приложения линейного программирования Матрица потребности в ресурсах для обеспечения единичного объёма производства в
- 57. /23 3.4. Экономические приложения линейного программирования Вектор цен продукции (за вычетом НДС), руб./ед. Вектор цен ресурсов
- 58. Применение линейного программирования в математических моделях (с) Н.М. Светлов, 2007 /23 3.5. Программное обеспечение линейного программирования
- 60. Скачать презентацию











































 Труд в изобразительном искусстве Выполнила учитель ИЗО Шаньшерова М.М. г. Белоярский ХМАО-Югра
Труд в изобразительном искусстве Выполнила учитель ИЗО Шаньшерова М.М. г. Белоярский ХМАО-Югра Лёгочные диссеминации
Лёгочные диссеминации  Бурильная колонна. КНБК. Работа бурильной колонны в скважине. Семинар 5
Бурильная колонна. КНБК. Работа бурильной колонны в скважине. Семинар 5 Происхождение и быт восточных славян
Происхождение и быт восточных славян Основы цветоведения
Основы цветоведения Паличкоподібні (циліндричні) бактерії Паличкоподібні бактерії мають форму паличок. Розрізняються різноманітністю розмірів,
Паличкоподібні (циліндричні) бактерії Паличкоподібні бактерії мають форму паличок. Розрізняються різноманітністю розмірів,  Качество товаров
Качество товаров Свойства нейтрино.
Свойства нейтрино. Русская культура конца XIII – XVI веков
Русская культура конца XIII – XVI веков Выращивание зелёного лука в различных условиях Выполнила: ученица 1 «Б» класса Атаманчук Даша Руководитель: Бояринкова Н. А.
Выращивание зелёного лука в различных условиях Выполнила: ученица 1 «Б» класса Атаманчук Даша Руководитель: Бояринкова Н. А. Искусство портрета
Искусство портрета Выполнила : Гавриленко Любовь Александровна. Вклад И.М. Сеченова в развитие мировой и отечественной физиологии.
Выполнила : Гавриленко Любовь Александровна. Вклад И.М. Сеченова в развитие мировой и отечественной физиологии.  47d45de70c3e43edaa4fce632df1ab97 (3)
47d45de70c3e43edaa4fce632df1ab97 (3) В художественном мире русской волшебной сказки Цикл «Развивающие исследовательские технологии». © Г.С. Меркин, 2009 г.
В художественном мире русской волшебной сказки Цикл «Развивающие исследовательские технологии». © Г.С. Меркин, 2009 г. «Банкир – это центральная фигура. Он держит на своих плечах весь мир.» Герберт Кэссон
«Банкир – это центральная фигура. Он держит на своих плечах весь мир.» Герберт Кэссон Евфимий Васильевич Путятин - русский адмирал
Евфимий Васильевич Путятин - русский адмирал Семинар «Воспитание личности школьника – важнейшее условие оптимизации образовательного процесса»
Семинар «Воспитание личности школьника – важнейшее условие оптимизации образовательного процесса»  Лучевая энергия Солнца и Т среды обитания животных
Лучевая энергия Солнца и Т среды обитания животных  Гемостаз
Гемостаз Банковские риски и управление ими Гурина Л.А.
Банковские риски и управление ими Гурина Л.А.  ГРАММАТИКА В СИСТЕМНОМ ПРЕДСТАВЛЕНИИ ЯЗЫКА
ГРАММАТИКА В СИСТЕМНОМ ПРЕДСТАВЛЕНИИ ЯЗЫКА Презентация Правовые и нормативные основы охраны труда
Презентация Правовые и нормативные основы охраны труда Инженерные сооружения на автомобильных дорогах
Инженерные сооружения на автомобильных дорогах Brainstorm. Project students’ activity
Brainstorm. Project students’ activity ЧЕЛОВЕК И ЕГО ДЕЯТЕЛЬНОСТЬ1
ЧЕЛОВЕК И ЕГО ДЕЯТЕЛЬНОСТЬ1 Навигатор дополнительного образования. Инструкция для родителей по регистрации на сайте
Навигатор дополнительного образования. Инструкция для родителей по регистрации на сайте «ДОБРЫХ РУК МАСТЕРСТВО». Публичное выступление – представление исследовательского проекта о произведениях декоративно-прик
«ДОБРЫХ РУК МАСТЕРСТВО». Публичное выступление – представление исследовательского проекта о произведениях декоративно-прик Михаил Юрьевич Лермонтов
Михаил Юрьевич Лермонтов