Содержание
- 2. 1. Общие положения Содержание 2. Момент силы относительно оси 3. Тренировочные задания 4. Применение теоремы Вариньона
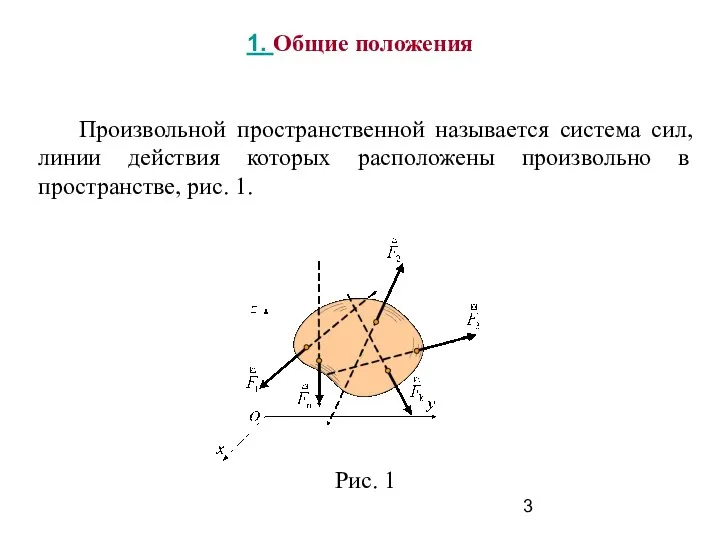
- 3. 1. Общие положения Произвольной пространственной называется система сил, линии действия которых расположены произвольно в пространстве, рис.
- 4. Произвольная пространственная система сил может быть приведена к силе, равной главному вектору и приложенной в произвольном
- 5. При равновесии тела под действием произвольной пространственной системы сил выполняются векторные условия: Из векторных условий равновесия
- 6. 2. Момент силы относительно оси Момент силы относительно оси характеризует враща-тельную способность силы относительно выбранной оси,
- 7. Момент силы относительно оси равен нулю в следующих случаях: 1) сила параллельна оси; 2) сила и
- 8. строим плоскость, перпендикулярную оси, которая составляет с плоскостью угол α;
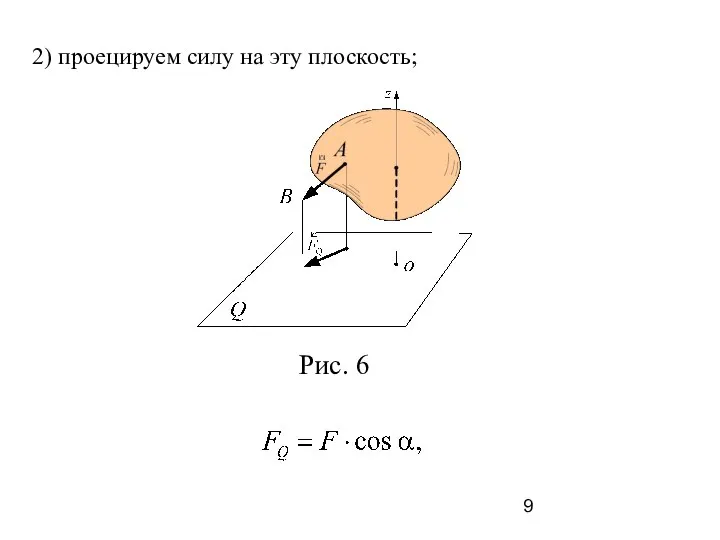
- 9. 2) проецируем силу на эту плоскость;
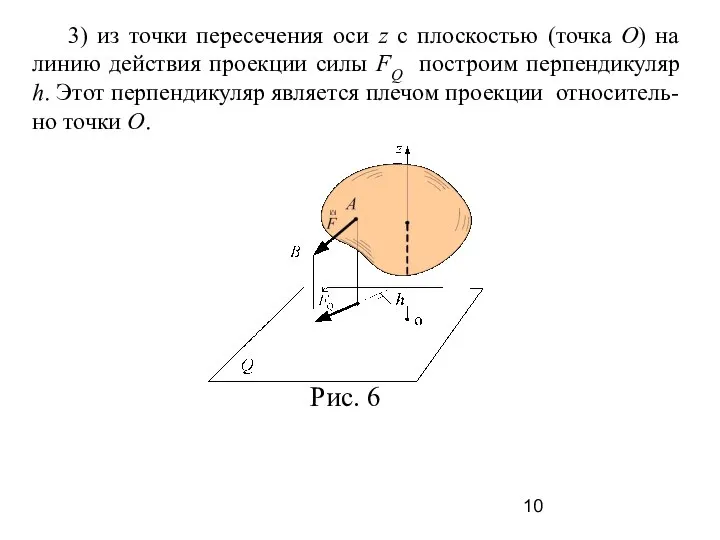
- 10. 3) из точки пересечения оси z с плоскостью (точка О) на линию действия проекции силы FQ
- 11. 4) найдём величину момента силы относительно оси z;
- 12. 5) определяем знак момента. Момента силы имеет знак (+), если с положительного конца оси поворот, который
- 13. Пример 2. На вал с маховиком, радиус которого равен r (рис. 4), действует сила . Требуется
- 14. Для определения момента силы относительно оси x построим проекцию вала и силы на плоскость, перпендикуляр-ную этой
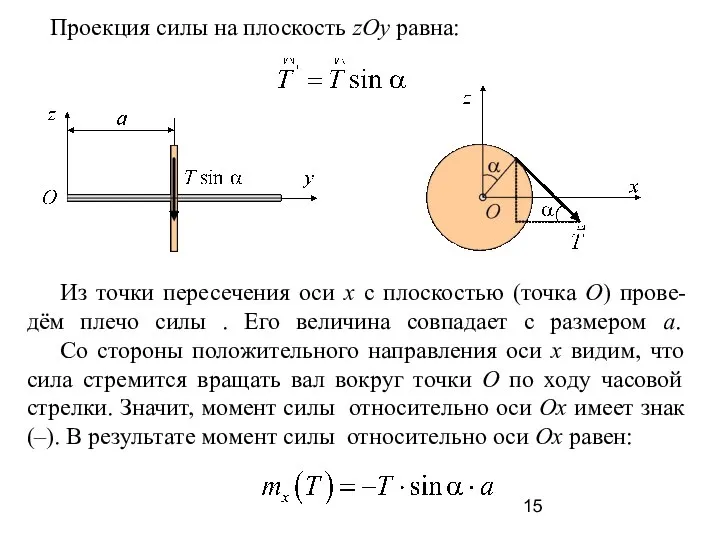
- 15. Проекция силы на плоскость zOy равна: Из точки пересечения оси x с плоскостью (точка О) прове-дём
- 16. Чтобы определить момент рассматриваемой силы относительно оси y, построим проекцию вала и силы на плоскость, перпендикулярную
- 17. Со стороны положительного направления оси y видно, что проекция силы стремится создать вращение вала относительно точки
- 18. Чтобы найти момент силы относительно оси z, построим проекцию вала и силы на плоскость, перпендикулярную оси
- 19. Со стороны положительного направления оси z видим, что проекция силы стремится создать вращение вала относительно точки
- 20. 3. Тренировочные задания Задание 1. К параллелепипеду на рис. 8, стороны которого равны a, b и
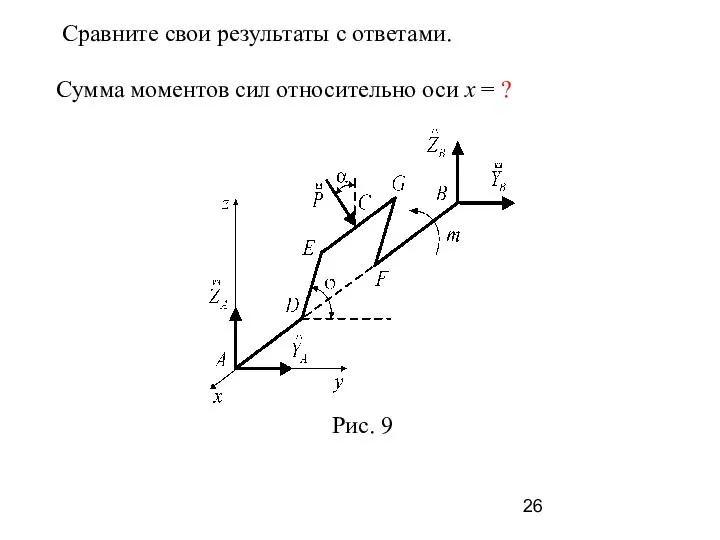
- 25. Задание 2. Ось коленчатого вала (рис. 9) расположена вдоль оси x и удерживается в равновесии реакциями
- 26. Сравните свои результаты с ответами. Сумма моментов сил относительно оси x = ?
- 27. Построим вид вала с положительной стороны оси x. Разложим силу P на составляющие и для определения
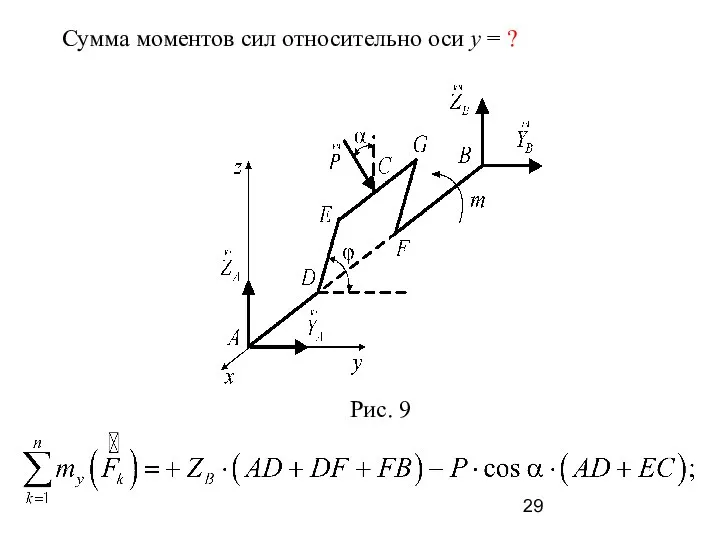
- 29. Сумма моментов сил относительно оси y = ?
- 30. Сумма моментов сил относительно оси z = ?
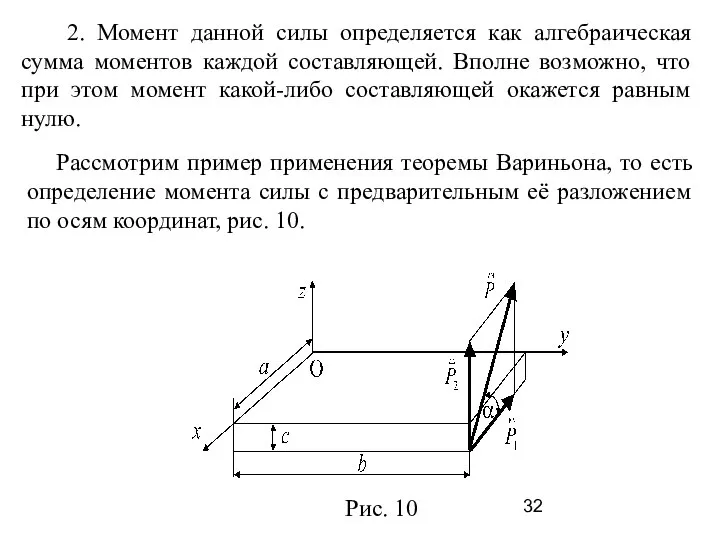
- 31. 4. Применение теоремы Вариньона Если известны углы наклона силы к плоскостям коорди-натных осей, то для вычисления
- 32. 2. Момент данной силы определяется как алгебраическая сумма моментов каждой составляющей. Вполне возможно, что при этом
- 33. где . По теореме Вариньона Находим моменты составляющих:
- 34. Таким образом,
- 35. Относительно оси z:
- 36. При решении задач будем придерживаться следующего плана. 1. Выбрать тело (конструкцию, узел конструкции), равно-весие которого необходимо
- 37. Рассмотрим примеры решения задач на равновесие тела под действием пространственной произвольной системы сил.
- 39. Решение Дано: d = 0,2 м.; D = 1 м.; Р=15 кН. Определить Q, реакции опор
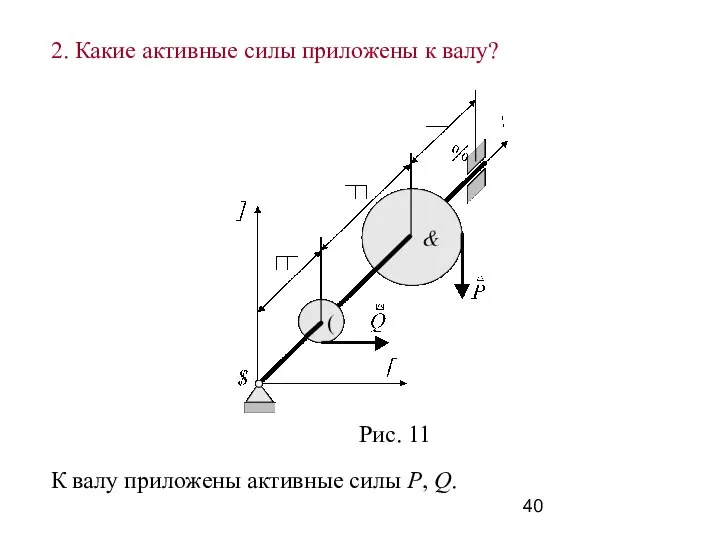
- 40. К валу приложены активные силы P, Q. 2. Какие активные силы приложены к валу?
- 41. 3. Как называются связи, действующие на вал? Вал имеет две связи: сферический шарнир А и цилиндричес-кий
- 42. 5. Как направлена сила реакции сферического шарнира A? Cила реакции сферического шарнира представляет собой вектор, направленный
- 43. 6. Как направлена сила реакции цилиндрического шарнира В? Cила реакции цилиндрического шарнира В представляет собой вектор,
- 44. 7. Как называется система сил, действующая на вал AB? На вал АВ действует пространственная произвольная система
- 45. 8. Какие уравнения равновесия можно составить для прос-транственной произвольной системы сил? Для пространственной произвольной системы сил
- 46. Составьте первое уравнение: Составьте второе уравнение: Составьте третье уравнение?
- 47. Составьте четвёртое уравнение. Составьте пятое уравнение. Составьте шестое уравнение.
- 48. Находим неизвестные силы из уравнений (1) – (6): из (2): YА = 0;
- 49. Знак «минус» у ХА и ХВ означает, что направления этих реакций противоположны направлениям, указанным на расчётной
- 50. 1. Коленчатый вал АВ расположен в горизонтальной плоскости. Нагружен силой F и моментом М, которые действуют
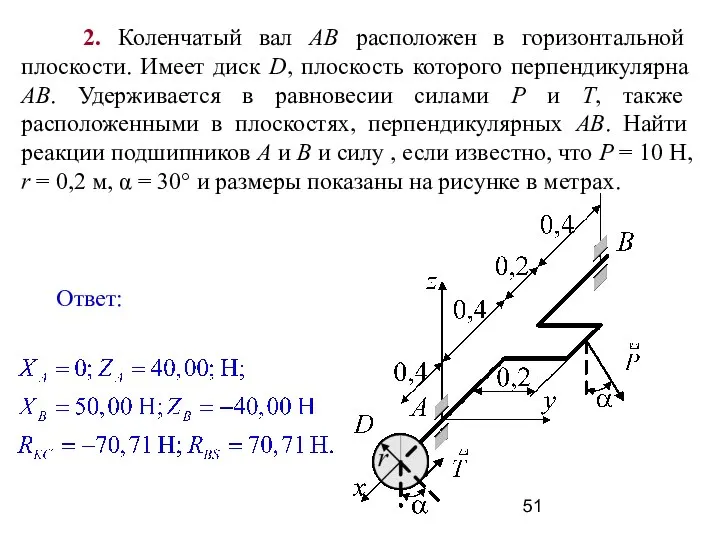
- 51. 2. Коленчатый вал АВ расположен в горизонтальной плоскости. Имеет диск D, плоскость которого перпендикулярна АВ. Удерживается
- 52. 3. Прямоугольная плита весом Р укреплена в горизонтальном положении с помощью шарнира А, стержней CN и
- 53. 4. Дано: P = 100 H, Q = 50 Н, CD = 3 м, CB =
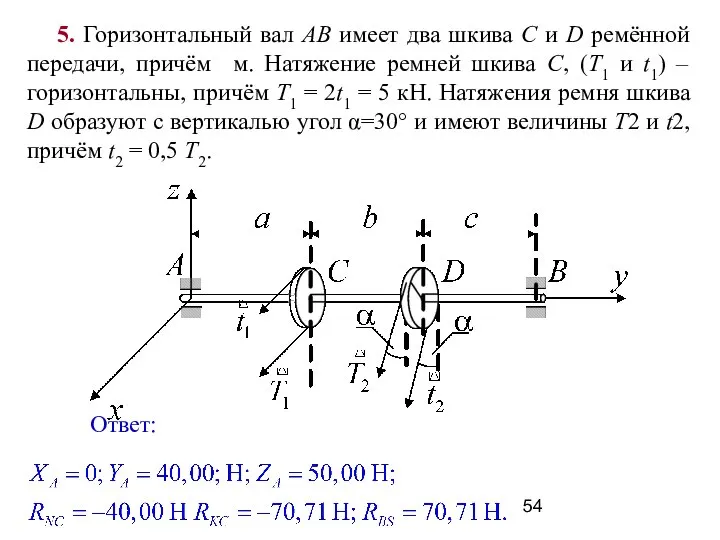
- 54. 5. Горизонтальный вал АВ имеет два шкива С и D ремённой передачи, причём м. Натяжение ремней
- 56. Скачать презентацию





















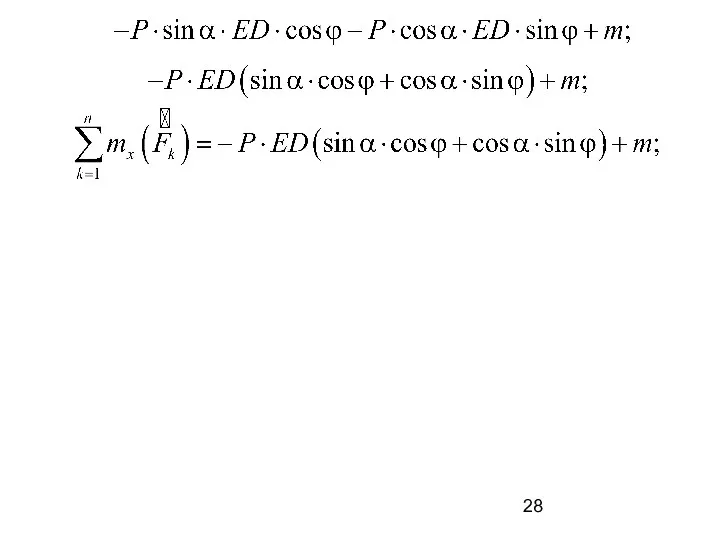





















 Русское народное зодчество
Русское народное зодчество Menedżer jako podmiot zarządzania
Menedżer jako podmiot zarządzania Анна Степановна Демидова
Анна Степановна Демидова Алгоритмы и исполнители
Алгоритмы и исполнители Презентация "Бюджет Российской Федерации" - скачать презентации по Экономике
Презентация "Бюджет Российской Федерации" - скачать презентации по Экономике Презентация по алгебре Линейная функция
Презентация по алгебре Линейная функция  Презентация КОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ С ИНОСТРАННЫМИ ИНВЕСТИЦИЯМИ
Презентация КОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ С ИНОСТРАННЫМИ ИНВЕСТИЦИЯМИ  Система Техническое обслуживание и ремонт оборудования
Система Техническое обслуживание и ремонт оборудования Разработка рабочих учебных программ педагогами образовательных учреждений
Разработка рабочих учебных программ педагогами образовательных учреждений Исчезающие животные (Англ)
Исчезающие животные (Англ)  Презентация Общие положения о таможенных процедурах в таможенном союзе
Презентация Общие положения о таможенных процедурах в таможенном союзе Классификация глосситов
Классификация глосситов Астрономия - древнейшая из наук
Астрономия - древнейшая из наук  Презентация Разработка миссии, целей и стратегии на примере фирмы «Полярис»
Презентация Разработка миссии, целей и стратегии на примере фирмы «Полярис» Ангиографические системы Toshiba Infinix и GE Innova. Основные компоненты, особенности эксплуатации
Ангиографические системы Toshiba Infinix и GE Innova. Основные компоненты, особенности эксплуатации My idol is Novak Djokovic
My idol is Novak Djokovic Проведение закупок по 223-ФЗ в электронной форме
Проведение закупок по 223-ФЗ в электронной форме Муниципальное общеобразовательное учреждение Белоносовская средняя общеобразовательная школа Урок обществознания в 10 классе
Муниципальное общеобразовательное учреждение Белоносовская средняя общеобразовательная школа Урок обществознания в 10 классе  организация работы детской поликлиники
организация работы детской поликлиники Мультиязычный интернет-каталог с автоматическим наполнением номенклатуры
Мультиязычный интернет-каталог с автоматическим наполнением номенклатуры «Папа, мама, я – спортивная семья». Спортивный праздник средняя школа №29
«Папа, мама, я – спортивная семья». Спортивный праздник средняя школа №29 Активний туризм як соціальне явище. Туризм: поняття та аспекти дослідження (Лекція №1)
Активний туризм як соціальне явище. Туризм: поняття та аспекти дослідження (Лекція №1) Портрет. Изучение нового материала
Портрет. Изучение нового материала Государственная гражданская служба
Государственная гражданская служба Программа кандидата на должность помощника депутата государственной думы РФ
Программа кандидата на должность помощника депутата государственной думы РФ Авиационные генераторы постоянного тока. (Тема 3.2)
Авиационные генераторы постоянного тока. (Тема 3.2) Роль библиотеки в лицензировании и аккредитации вуза
Роль библиотеки в лицензировании и аккредитации вуза  Предварительное расследование и его формы
Предварительное расследование и его формы