Содержание
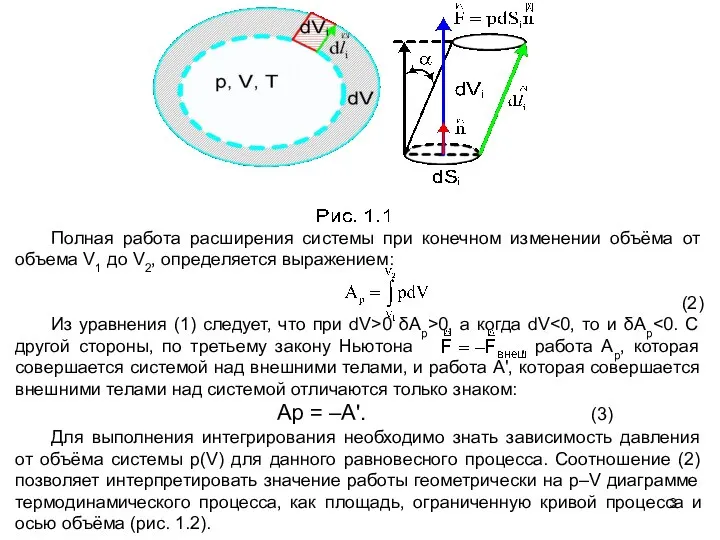
- 2. Пусть в системе частиц происходит какой-либо равновесный термодинамический процесс, сопровождающийся малым изменением объёма системы (рис. 1.1).
- 3. Полная работа расширения системы при конечном изменении объёма от объема V1 до V2, определяется выражением: (2)
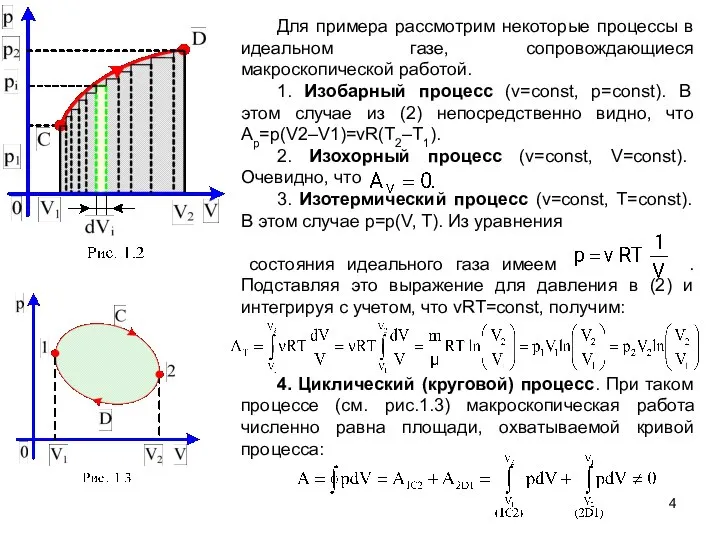
- 4. Для примера рассмотрим некоторые процессы в идеальном газе, сопровождающиеся макроскопической работой. 1. Изобарный процесс (ν=const, p=const).
- 5. Работа при круговом процессе есть заштрихованная на диаграмме (1.3) площадь. Работа положительна, если процесс на p–V-
- 6. 1.3. Внутренняя энергия. Первое начало термодинамики. Одним из основных законов природы, установленный на основе опытов и
- 7. Отсюда следует, что значение интеграла между состояниями 1 и 2 не зависит от рода процесса, а
- 8. Перечислим свойства внутренней энергии: 1) Внутренняя энергия является функцией состояния. 2) Внутренняя энергия определена с точностью
- 9. 1.4. Внутренняя энергия идеального газа. Согласно определению идеального газа, молекулы не взаимодействуют друг с другом, за
- 10. С учетом этого, соотношение для внутренней энергии идеального газа примет вид: (10) Использую уравнение Менделеева –
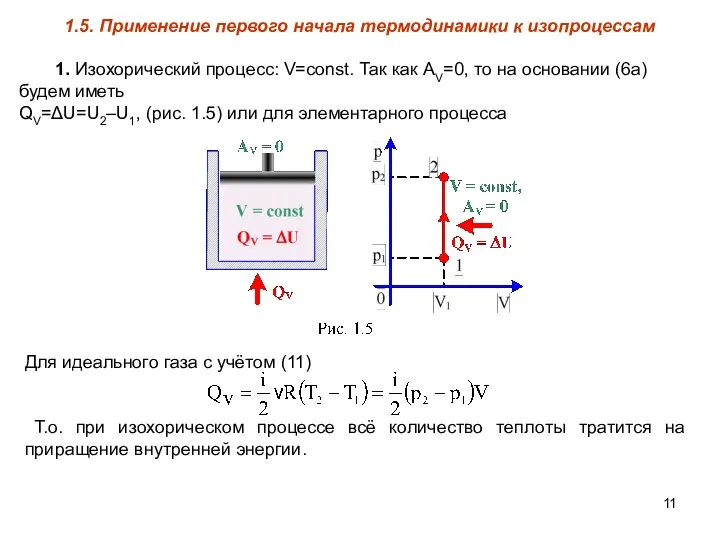
- 11. 1.5. Применение первого начала термодинамики к изопроцессам 1. Изохорический процесс: V=const. Так как АV=0, то на
- 12. 2. Изобарический процесс: p=const. При изобарическом процессе изменяется и температура и объем газа. Следовательно Qp=ΔU+Ap=ΔU+p(V2–V1), или
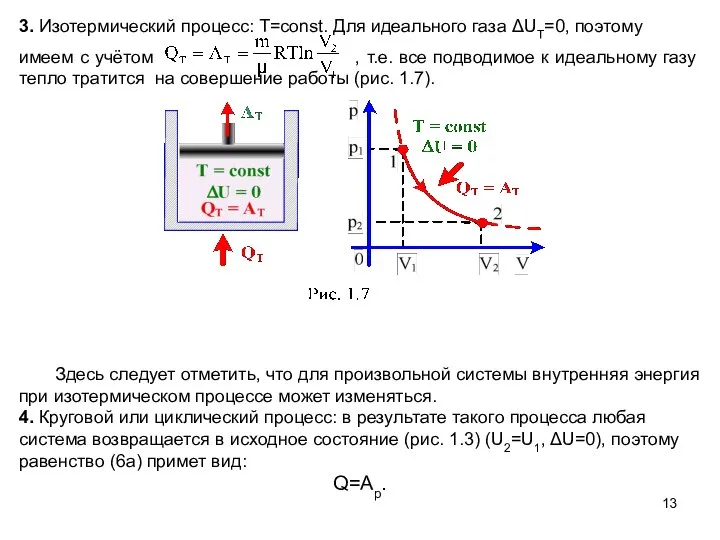
- 13. 3. Изотермический процесс: T=const. Для идеального газа ΔUT=0, поэтому имеем с учётом , т.е. все подводимое
- 14. 5. Адиабатический процесс – процесс в термодинамической системе, происходящий без теплообмена с окружающей средой (Q=0), а
- 15. ОСНОВЫ ТЕРМОДИНАМИКИ -2. 2.1 Теплоемкость системы. Классическая теория теплоемкости и ее ограниченность. Теплоемкостью системы называется величина,
- 16. Изотермический процесс. Т= const, dT =0. Вся тепловая энергия, полученная системой ( или отданная ) идет
- 17. Адиабатический процесс. Это процесс, протекающий в изолированной системе, теплообмен с внешней средой отсутствует, , а изменение
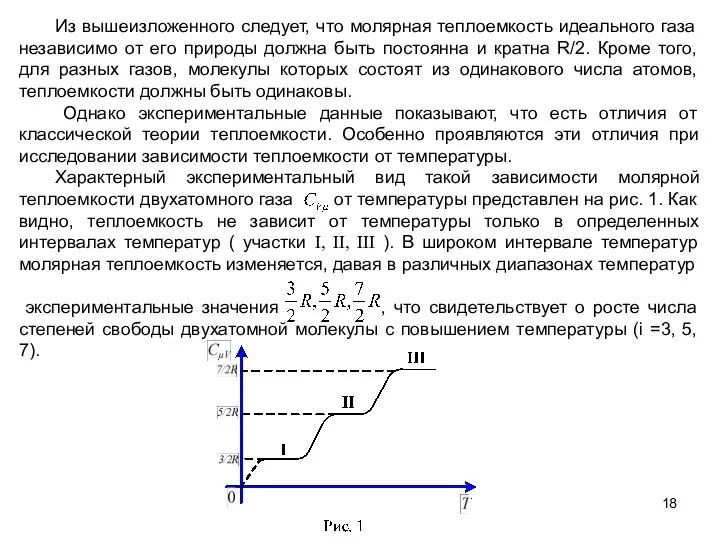
- 18. Из вышеизложенного следует, что молярная теплоемкость идеального газа независимо от его природы должна быть постоянна и
- 19. При низких температурах для поведения молекул характерно поступательное движение (участок I), по мере роста температуры (нормальные
- 20. Энергетические уровни, соответствующие определенному виду движения, возбуждаются в среднем при температурах не ниже: которые находятся в
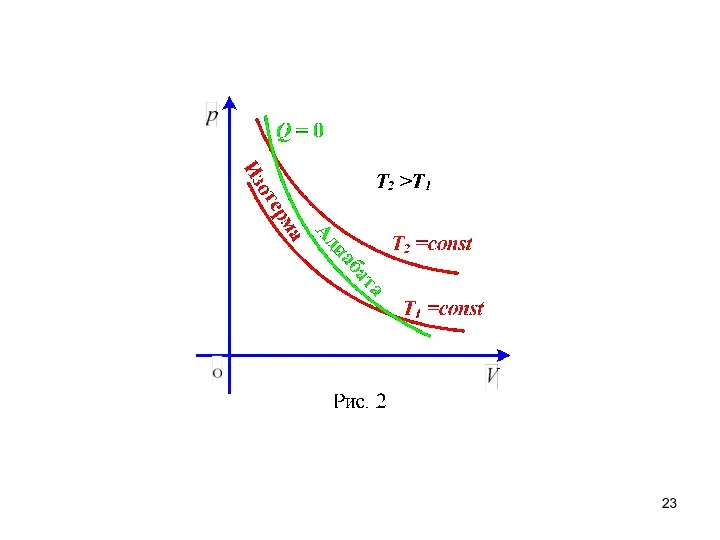
- 21. 2.2 Адиабатический процесс. Уравнение Пуассона. Получим уравнение равновесного адиабатического процесса для идеального газа. На основании I
- 22. После интегрирования обеих частей уравнения получим: или (здесь С- константа интегрирования). Итак, уравнение Пуассона для равновесного
- 25. Скачать презентацию
















 Презентация "Андрей Матвеев" - скачать презентации по МХК
Презентация "Андрей Матвеев" - скачать презентации по МХК Die Zeit
Die Zeit . Экомониторинг
. Экомониторинг Հայկազուն-Երվանդունիների թագավորություն (6)
Հայկազուն-Երվանդունիների թագավորություն (6) German Customs and Traditions
German Customs and Traditions Ноябрь – зиме родной брат
Ноябрь – зиме родной брат Леонард Эйлер. Круги Эйлера
Леонард Эйлер. Круги Эйлера Шағын бизнес
Шағын бизнес Концепция подготовки спортивного резерва в РФ до 2025
Концепция подготовки спортивного резерва в РФ до 2025 Презентация "Государственное регулирование цен" - скачать презентации по Экономике
Презентация "Государственное регулирование цен" - скачать презентации по Экономике Mitsubishi Galant VIII - история автомобиля
Mitsubishi Galant VIII - история автомобиля Католическая церковь
Католическая церковь Презентация Дальневосточное Таможенное управление
Презентация Дальневосточное Таможенное управление Третейское разбирательство. Нотариат в Российской Федерации
Третейское разбирательство. Нотариат в Российской Федерации ТЕРМОРЕГУЛЯЦИЯ
ТЕРМОРЕГУЛЯЦИЯ Меры социальной поддержки по ЖКУ. Субсидии
Меры социальной поддержки по ЖКУ. Субсидии Этапы создания текста перевода
Этапы создания текста перевода Взаимоотношения с риелторскими службами
Взаимоотношения с риелторскими службами Оборудование плавильного участка
Оборудование плавильного участка Микробиология сальмонеллезов
Микробиология сальмонеллезов Вибрационные методы
Вибрационные методы Пампа Моняк
Пампа Моняк Культура и поведение
Культура и поведение Туристский клуб «Белки». Первый сплав по Берди - «Первооткрыватель»
Туристский клуб «Белки». Первый сплав по Берди - «Первооткрыватель» Cyber Spying in world today
Cyber Spying in world today OptoGaN Enabling bulb-like brightness for LEDs
OptoGaN Enabling bulb-like brightness for LEDs Виды отклонений от языковой нормы и их передача
Виды отклонений от языковой нормы и их передача Отделение электроники. Лидский колледж
Отделение электроники. Лидский колледж