Содержание
- 2. Понятие о методах Монте-Карло При исследовании взаимодействующих систем расчет термодинамических средних методом точной диагонализации при достаточно
- 3. Простейший пример: вычисление площади сложной плоской фигуры Поместим фигуру внутрь единичного квадрата Выберем внутри квадрата N
- 4. Расчет интегралов Требуется вычислить интеграл Выберем произвольную плотность распределения, удовлетворяющую условию Определим случайную величину – случайная
- 5. Расчет интегралов Для оптимального расчета интеграла с минимальной погрешностью следует выбирать распределение p(x), пропорциональное |g(x)| или,
- 6. Расчет интегралов Рассчитаем методом Монте-Карло интеграл Используем для расчета интеграла различные нормированные функции распределения:
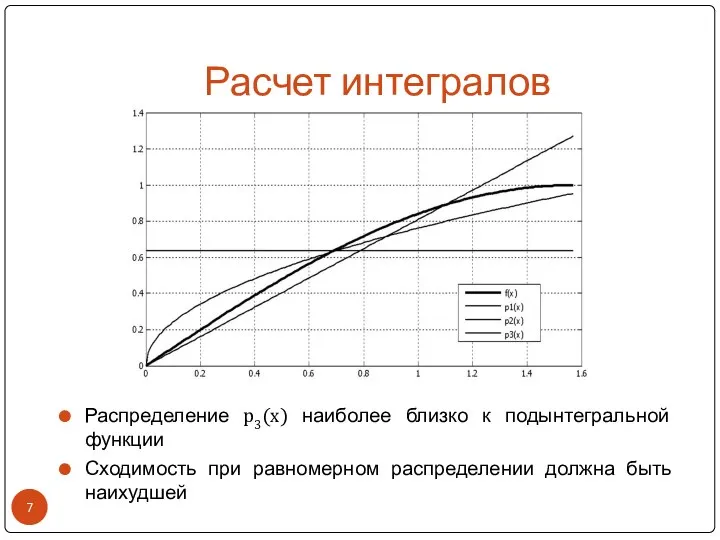
- 7. Расчет интегралов Распределение p3(x) наиболее близко к подынтегральной функции Сходимость при равномерном распределении должна быть наихудшей
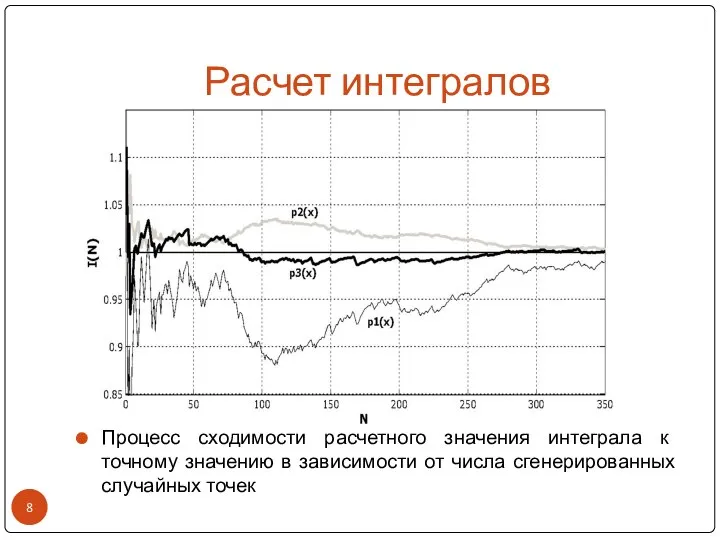
- 8. Расчет интегралов Процесс сходимости расчетного значения интеграла к точному значению в зависимости от числа сгенерированных случайных
- 10. Скачать презентацию





 Синхронное плавание - грации России
Синхронное плавание - грации России Теория формирования научных понятий у младших школьников
Теория формирования научных понятий у младших школьников Триумфальная арка Санкт-Петербурга – Московские Триумфальные ворота Презентация выполнена студенткой 2А группы Андреевой Тама
Триумфальная арка Санкт-Петербурга – Московские Триумфальные ворота Презентация выполнена студенткой 2А группы Андреевой Тама Презентация Программа аудита экспортных операций
Презентация Программа аудита экспортных операций Прилади акустоелектроніки. Перетворювачі. Детектори. Відбивачі. Концентратори. Відгалужувачі
Прилади акустоелектроніки. Перетворювачі. Детектори. Відбивачі. Концентратори. Відгалужувачі Фёдор Михайлович Достоевский
Фёдор Михайлович Достоевский Профилактика преступлений против половой неприкосновенности несовершеннолетних
Профилактика преступлений против половой неприкосновенности несовершеннолетних Nuduri japoneze
Nuduri japoneze Моя любимая книга ‘’Робинзон Крузо’’. Даниель Дефо 1660-1731
Моя любимая книга ‘’Робинзон Крузо’’. Даниель Дефо 1660-1731 Участие в закупках по Федеральным законам в роли поставщика
Участие в закупках по Федеральным законам в роли поставщика Правила деловых отношений
Правила деловых отношений Проектирование цифровой системы телевещания
Проектирование цифровой системы телевещания Коренное население Республики Башкортостан
Коренное население Республики Башкортостан Интерфейсы взаимодействия в компьютерных играх
Интерфейсы взаимодействия в компьютерных играх История возникновения коктейлей
История возникновения коктейлей Итераторы и LINQ.
Итераторы и LINQ. Эволюция жизни
Эволюция жизни Первая в мире электрическая лампочка ( П.Н. Яблочков и А.Н. Лодыгин) Подготовили: студентки 2 курса группы Ю-123б Букшина Алексан
Первая в мире электрическая лампочка ( П.Н. Яблочков и А.Н. Лодыгин) Подготовили: студентки 2 курса группы Ю-123б Букшина Алексан Блиц-опрос Менеджмент
Блиц-опрос Менеджмент Презентация 1. Производственные процесс: сущность, типы, категории. 2. Основные принципы организации производства. 3. Организацион
Презентация 1. Производственные процесс: сущность, типы, категории. 2. Основные принципы организации производства. 3. Организацион Виктор Федорович Янукович - президент Украины с 25 февраля 2010 года по 22 февраля 2014 года
Виктор Федорович Янукович - президент Украины с 25 февраля 2010 года по 22 февраля 2014 года Моделирование и визуализация cлучайных данных
Моделирование и визуализация cлучайных данных Программирование. Базовый курс 2 часть
Программирование. Базовый курс 2 часть Объединение «Народная традиция». Капустник
Объединение «Народная традиция». Капустник Системный метод научных исследований Подготовили: студентки 2 курса группы Ю-123б Букшина Александра, Простакова Вероника
Системный метод научных исследований Подготовили: студентки 2 курса группы Ю-123б Букшина Александра, Простакова Вероника Педагогический совет по катехизации
Педагогический совет по катехизации История футбола в России
История футбола в России Основы медицинской антропологии
Основы медицинской антропологии