Содержание
- 2. Элементы линейной алгебры и геометрии выпуклых множеств Теоретические основы методов линейного программирования
- 3. Элементы линейной алгебры Пусть дана система линейных уравнений c переменными (*) - ранг матрицы, то есть
- 4. Элементы линейной алгебры Пусть дана система линейных уравнений c переменными (*) - ранг матрицы, то есть
- 5. Элементы линейной алгебры Определение. Любые переменных называются базисными (или основными), если определитель матрицы (базисный минор), составленный
- 6. Элементы линейной алгебры Определение. Решение системы называется допустимым, если оно содержит только неотрицательные компоненты, в противном
- 7. Элементы линейной алгебры Определение. Решение системы называется допустимым, если оно содержит только неотрицательные компоненты, в противном
- 8. Элементы линейной алгебры Определение. Решение системы называется допустимым, если оно содержит только неотрицательные компоненты, в противном
- 9. Элементы линейной алгебры Определение. Решение системы называется допустимым, если оно содержит только неотрицательные компоненты, в противном
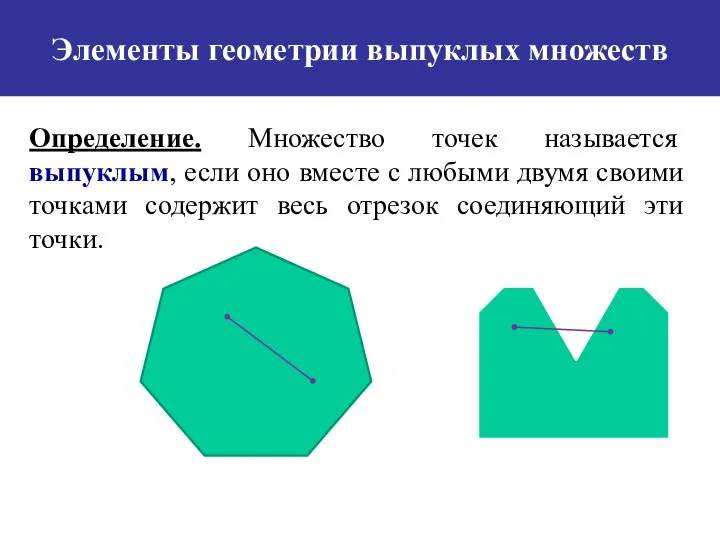
- 10. Элементы геометрии выпуклых множеств Определение. Множество точек называется выпуклым, если оно вместе с любыми двумя своими
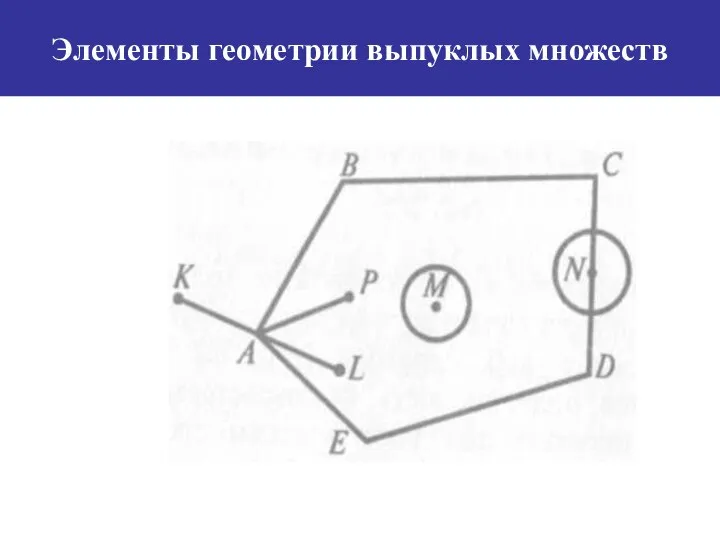
- 11. Элементы геометрии выпуклых множеств Определение. Точка множества называется внутренней, если в некоторой ее окрестности содержатся точки
- 12. Элементы геометрии выпуклых множеств
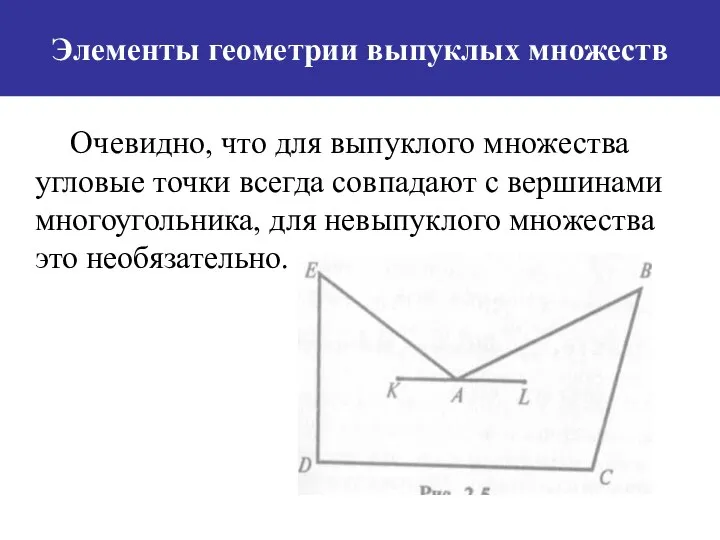
- 13. Элементы геометрии выпуклых множеств Очевидно, что для выпуклого множества угловые точки всегда совпадают с вершинами многоугольника,
- 14. Элементы геометрии выпуклых множеств Определение. Множество точек называется замкнутым, если включает все свои граничные точки. Определение.
- 15. Элементы геометрии выпуклых множеств Выпуклое замкнутое множество точек пространства (плоскости) имеющее конечное число угловых точек называется
- 16. Теоретические основы методов ЛП Множество всех допустимых решений задачи линейного программирования является выпуклым, а точнее, представляет
- 17. Теоретические основы методов ЛП Теорема. Если задача линейного программирования имеет оптимальное решение, то линейная функция принимает
- 18. Теоретические основы методов ЛП Теорема. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка многогранника
- 19. Теоретические основы методов ЛП Следствие. Если задача линейного программирования имеет оптимальное решение, то оно совпадает, по
- 20. Симплексный метод решения задач ЛП Джордж Данциг, 1947
- 21. Симплексный метод основывается область допустимых решений задачи линейного программирования является выпуклым множеством с конечным числом угловых
- 22. Симплексный метод основывается область допустимых решений задачи линейного программирования является выпуклым множеством с конечным числом угловых
- 23. Симплексный метод основывается область допустимых решений задачи линейного программирования является выпуклым множеством с конечным числом угловых
- 24. Симплексный метод состоит в целенаправленном переборе опорных решений задачи линейного программирования. Так как общее число опорных
- 25. Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многоугольника ограничений, которая называется первоначальной,
- 26. Основное содержание симплексного метода найти начальное опорное решение; осуществить переход от одного опорного решения к другому,
- 27. Основное содержание симплексного метода найти начальное опорное решение; осуществить переход от одного опорного решения к другому,
- 28. Основное содержание симплексного метода найти начальное опорное решение; осуществить переход от одного опорного решения к другому,
- 29. Симплексный метод решения задач ЛП Рассмотрим задачу ЛП в канонической форме: Пусть (иначе, умножим соответ-ствующее уравнение
- 30. Специальная форма задачи ЛП
- 31. Алгоритм симплекс-метода для задачи на минимум Шаг 0. Подготовительный этап. Шаг 1. Составляем симплекс-таблицу, соответствующую специальной
- 32. Шаг 0. Подготовительный этап Приводим задачу ЛП к специальной форме
- 33. Шаг 1. Составляем симплекс-таблицу, соответствующую специальной форме
- 34. Рассмотрим реализацию метода на следующем примере:
- 38. Шаг 0
- 39. Шаг 1. Составляем симплекс-таблицу, соответствующую специальной форме
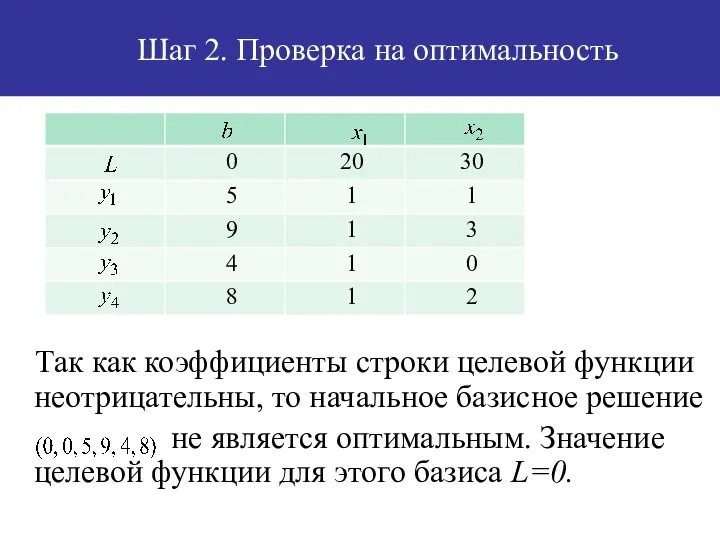
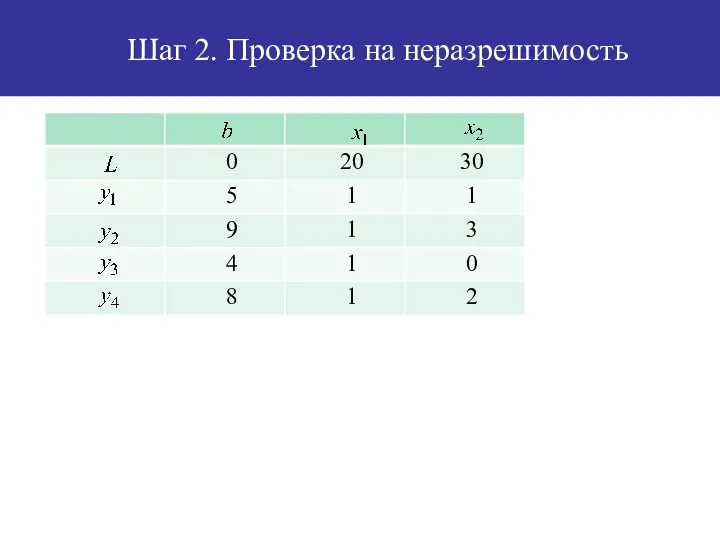
- 40. Шаг 2. Проверка на оптимальность Так как коэффициенты строки целевой функции неотрицательны, то начальное базисное решение
- 41. Шаг 2. Проверка на неразрешимость
- 42. Шаг 4. Выбор ведущего столбца q Ведущий столбец
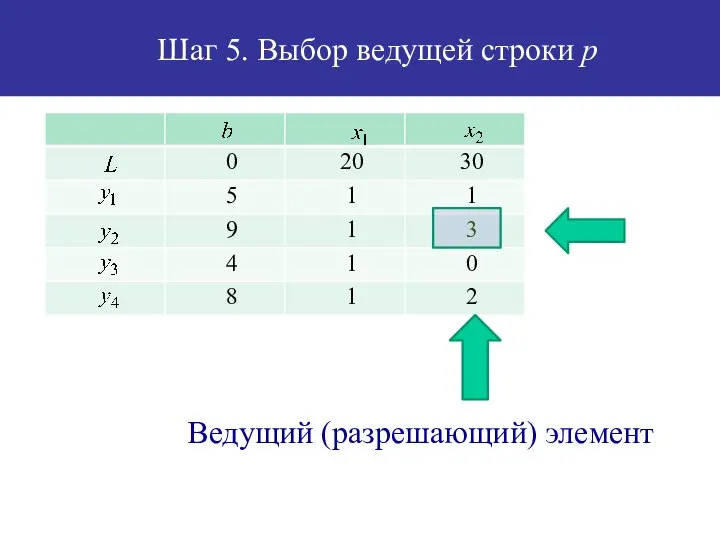
- 43. Шаг 5. Выбор ведущей строки p Ведущая строка
- 44. Шаг 5. Выбор ведущей строки p Ведущий (разрешающий) элемент
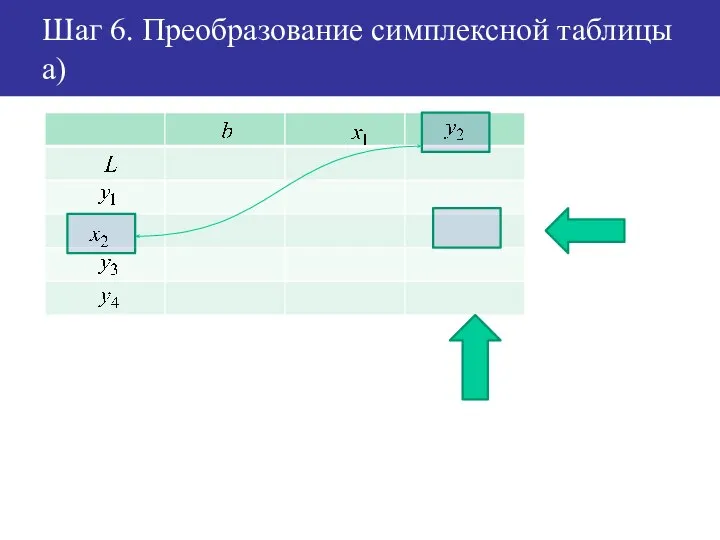
- 45. Шаг 6. Преобразование симплексной таблицы a)
- 46. Шаг 6. Преобразование симплексной таблицы б) Ведущий элемент заменяем обратной величиной
- 47. Шаг 6. Преобразование симплексной таблицы б) Ведущий элемент заменяем обратной величиной
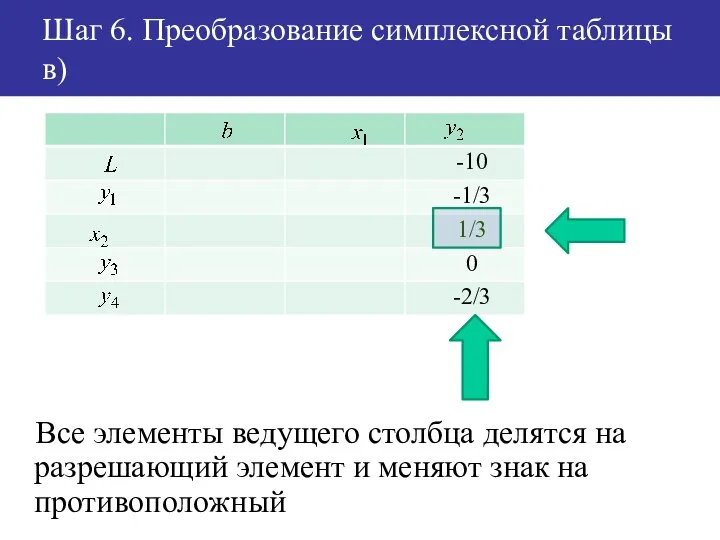
- 48. Шаг 6. Преобразование симплексной таблицы в) Все элементы ведущего столбца делятся на разрешающий элемент и меняют
- 49. Шаг 6. Преобразование симплексной таблицы в) Все элементы ведущего столбца делятся на разрешающий элемент и меняют
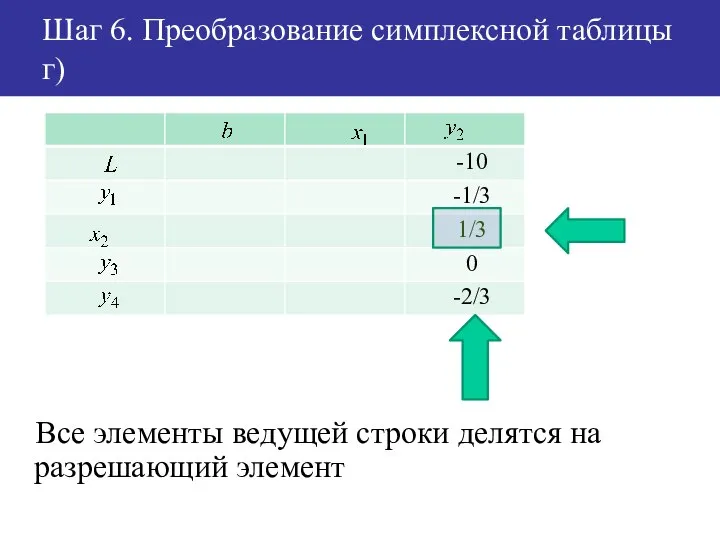
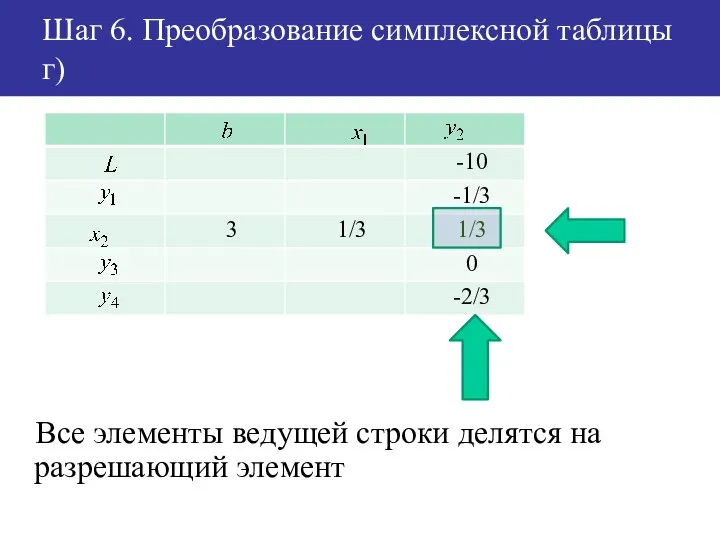
- 50. Шаг 6. Преобразование симплексной таблицы г) Все элементы ведущей строки делятся на разрешающий элемент
- 51. Шаг 6. Преобразование симплексной таблицы г) Все элементы ведущей строки делятся на разрешающий элемент
- 52. Шаг 6. Преобразование симплексной таблицы д) Оставшиеся элементы симплексной таблицы преобразуются по схеме «прямоугольника»
- 53. Шаг 6. Преобразование симплексной таблицы д) Схема прямоугольника
- 54. Шаг 6. Преобразование симплексной таблицы д) Опорное решение, соответствующее таблице Значение целевой функции на этом базисе
- 56. Скачать презентацию











































 Единая школьная карта
Единая школьная карта Технологии разработки ПО. Основные понятия и определения
Технологии разработки ПО. Основные понятия и определения НОВАЯ ЭКОНОМИЧЕСКАЯ АССОЦИАЦИЯ ВТОРОЙ РОССИЙСКИЙ ЭКОНОМИЧЕСКИЙ КОНГРЕСС БОРЬБА С УКЛОНЕНИЕМ ОТ УПЛАТЫ НАЛОГОВ И «НАЛОГОВЫМИ
НОВАЯ ЭКОНОМИЧЕСКАЯ АССОЦИАЦИЯ ВТОРОЙ РОССИЙСКИЙ ЭКОНОМИЧЕСКИЙ КОНГРЕСС БОРЬБА С УКЛОНЕНИЕМ ОТ УПЛАТЫ НАЛОГОВ И «НАЛОГОВЫМИ  CSS (Cascading Style Sheets)
CSS (Cascading Style Sheets) құндылық
құндылық Мохандас Карамчанд Ганди
Мохандас Карамчанд Ганди «Есть такая профессия – ученик»
«Есть такая профессия – ученик» Реабилитация. Возмещение вреда
Реабилитация. Возмещение вреда Общие сведения о языке программирования Паскаль
Общие сведения о языке программирования Паскаль Заболевания щитовидной железы
Заболевания щитовидной железы Электро Механик
Электро Механик Роспись яиц
Роспись яиц Презентация Социально-обеспечительные правоотношения
Презентация Социально-обеспечительные правоотношения  «TIS-Трудозатраты» Система учета занятости сотрудников. - презентация
«TIS-Трудозатраты» Система учета занятости сотрудников. - презентация умножение и деление на 8 - презентация для начальной школы
умножение и деление на 8 - презентация для начальной школы Web-программирование. Лекция 5. python 3 (часть 2)
Web-программирование. Лекция 5. python 3 (часть 2) Презентация "Макроэкономическая нестабильность и ее основные проявления" - скачать презентации по Экономике
Презентация "Макроэкономическая нестабильность и ее основные проявления" - скачать презентации по Экономике Стратегии тестирования
Стратегии тестирования «Закрепление внетабличного деления и умножения» Математика, 3 класс Учитель начальных классов Симбирева Дарья Викторовна, ГБОУ
«Закрепление внетабличного деления и умножения» Математика, 3 класс Учитель начальных классов Симбирева Дарья Викторовна, ГБОУ  Диаграммы классов. Объектно- ориентированное программирование. (Лекция 5)
Диаграммы классов. Объектно- ориентированное программирование. (Лекция 5) Комплексное оснащение предприятий ресторанного бизнеса на примере овощерезки Robot Coupe CL 50
Комплексное оснащение предприятий ресторанного бизнеса на примере овощерезки Robot Coupe CL 50 Христианская апологетика и история
Христианская апологетика и история Сервис Фото для участников MyWeb Фотохостинг на MyWeb http://myweb.kz/
Сервис Фото для участников MyWeb Фотохостинг на MyWeb http://myweb.kz/ Прогнозирование денежного потока инвестиционного проекта
Прогнозирование денежного потока инвестиционного проекта  Анализ алгоритмов. (Лекция 16)
Анализ алгоритмов. (Лекция 16) The military factor in contemporary international relation
The military factor in contemporary international relation Описание слайда:
Методики определения потребности в лекарственных средствах.
Описание слайда:
Методики определения потребности в лекарственных средствах. ЗАЩИТА АНАЛИТИЧЕСКОГО ОТЧЁТА Юдиной Ирины Николаевны воспитатель ГПД
ЗАЩИТА АНАЛИТИЧЕСКОГО ОТЧЁТА Юдиной Ирины Николаевны воспитатель ГПД