Содержание
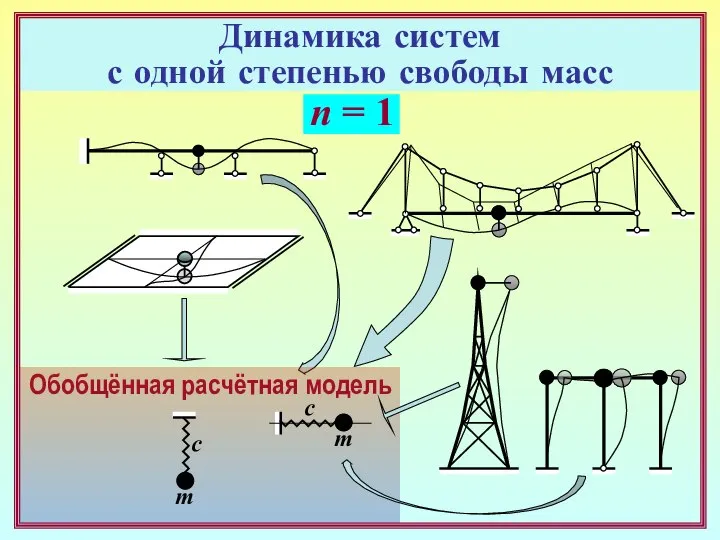
- 2. Обобщённая расчётная модель n = 1 m c m c Динамика систем с одной степенью свободы
- 3. Динамика систем с одной степенью свободы масс Предпосылки и рабочие гипотезы линейной теории динамических расчётов систем
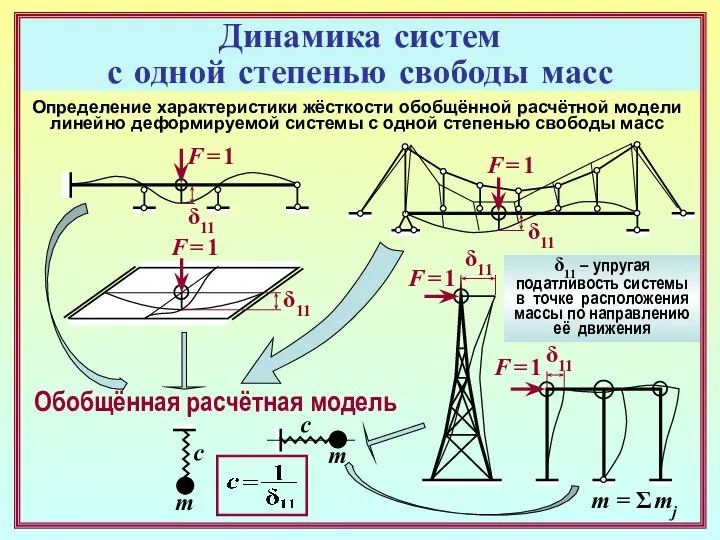
- 4. Обобщённая расчётная модель m c m c Динамика систем с одной степенью свободы масс Определение характеристики
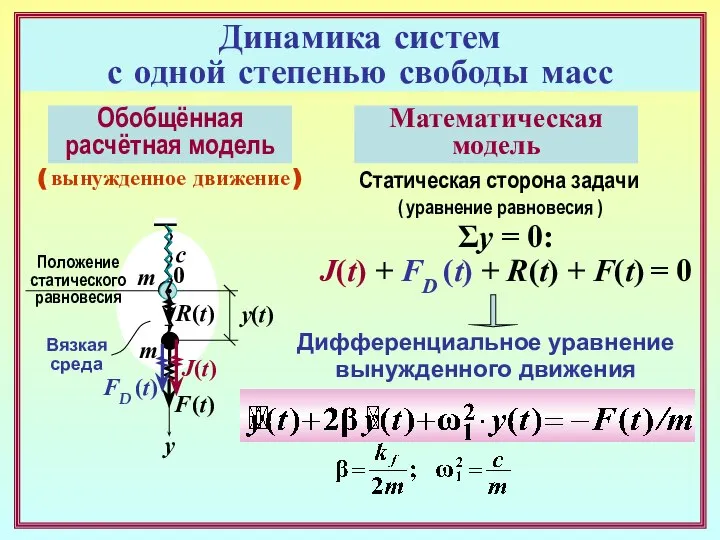
- 5. Динамика систем с одной степенью свободы масс Обобщённая расчётная модель m c Вязкая среда Положение статического
- 6. Динамика систем с одной степенью свободы масс Обобщённая расчётная модель Положение статического равновесия ( свободное движение
- 7. Решение дифференциального уравнения свободного движения системы с одной степенью свободы масс Характеристическое уравнение: Уравнение свободного движения
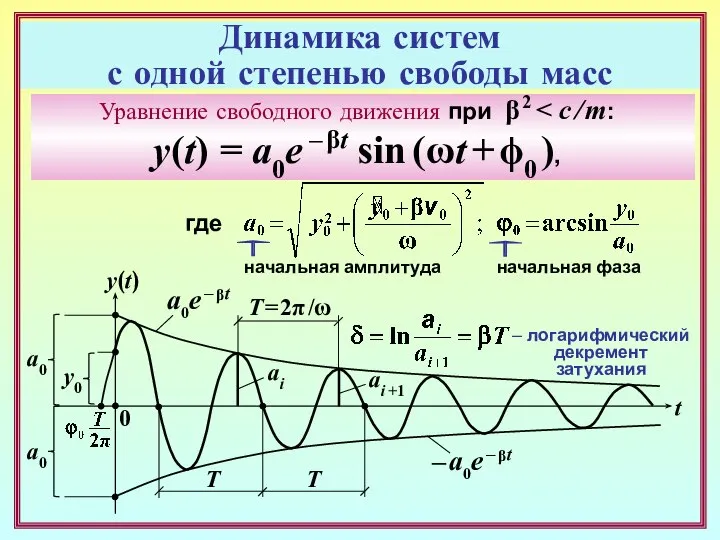
- 8. Динамика систем с одной степенью свободы масс Уравнение свободного движения при β 2 y(t) = a0e
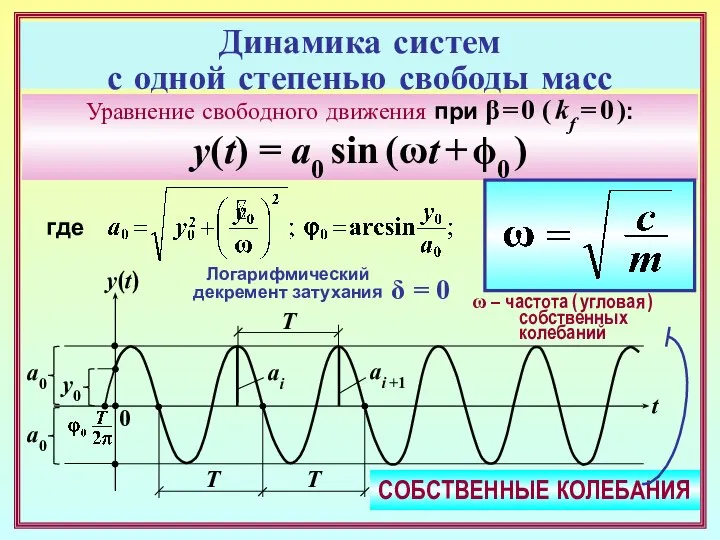
- 9. Динамика систем с одной степенью свободы масс Уравнение свободного движения при β = 0 ( kf
- 10. Динамика систем с одной степенью свободы масс Обобщённая расчётная модель m c Вязкая среда Положение статического
- 11. Динамика систем с одной степенью свободы масс a0e – βt sin (ωt + ϕ0 ) Решение
- 12. Динамика систем с одной степенью свободы масс t F(t) F F y*(t) = μ * yst,F
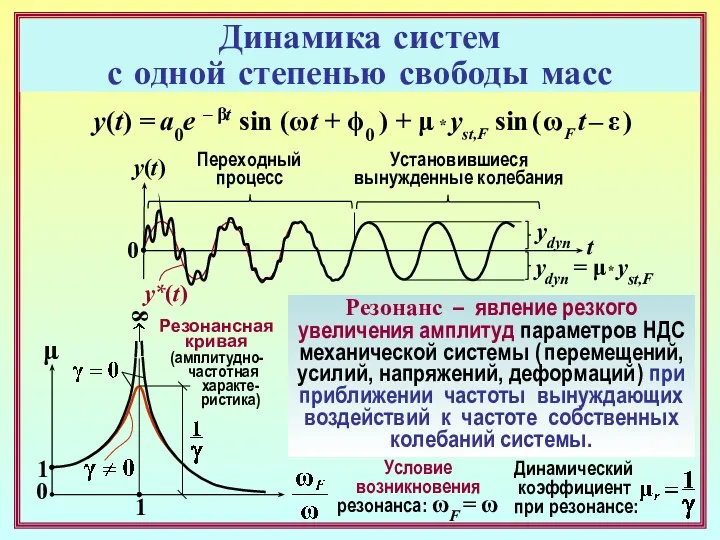
- 13. t y(t) ydyn y*(t) μ 0 ydyn = μ* yst,F Переходный процесс Установившиеся вынужденные колебания 0
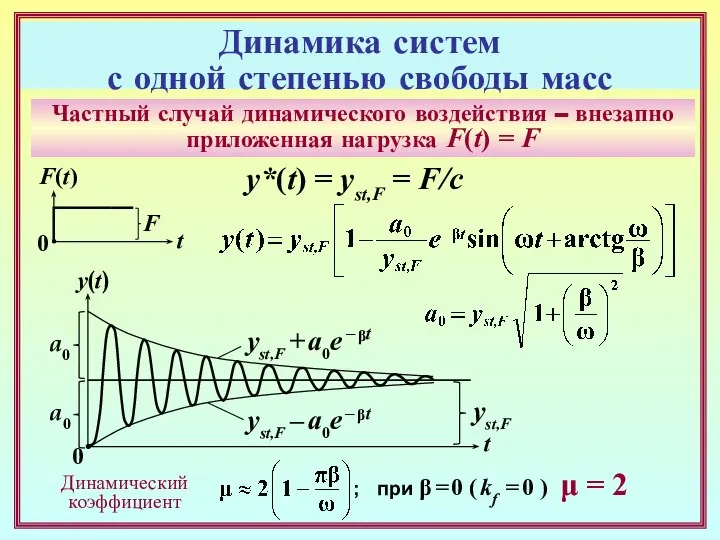
- 14. Динамика систем с одной степенью свободы масс Частный случай динамического воздействия – внезапно приложенная нагрузка F(t)
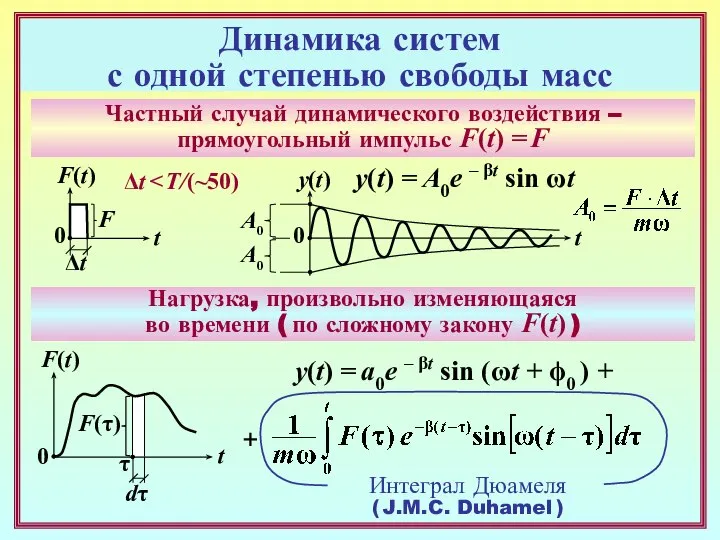
- 15. Динамика систем с одной степенью свободы масс Частный случай динамического воздействия –прямоугольный импульс F(t) = F
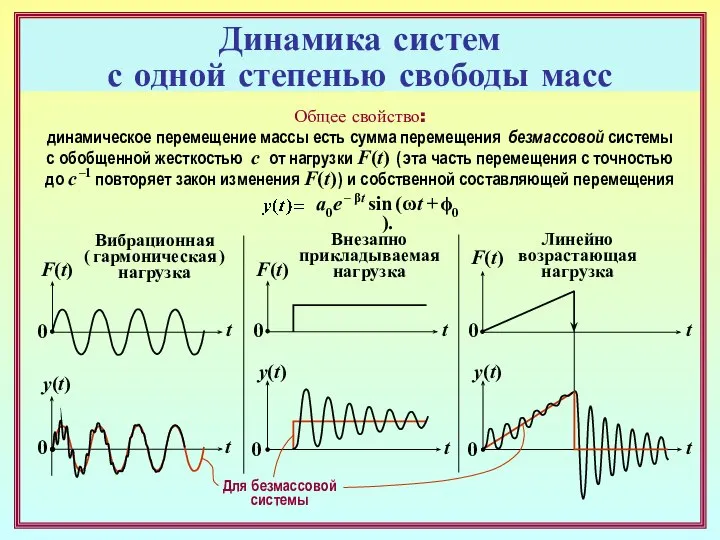
- 16. Динамика систем с одной степенью свободы масс Общее свойство: динамическое перемещение массы есть сумма перемещения безмассовой
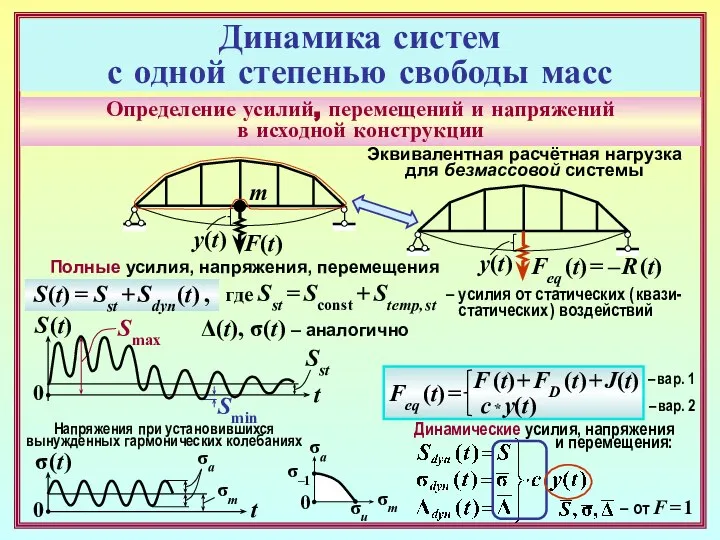
- 17. Определение усилий, перемещений и напряжений в исходной конструкции F(t) t 0 F(t) 0 t y(t) y(t)
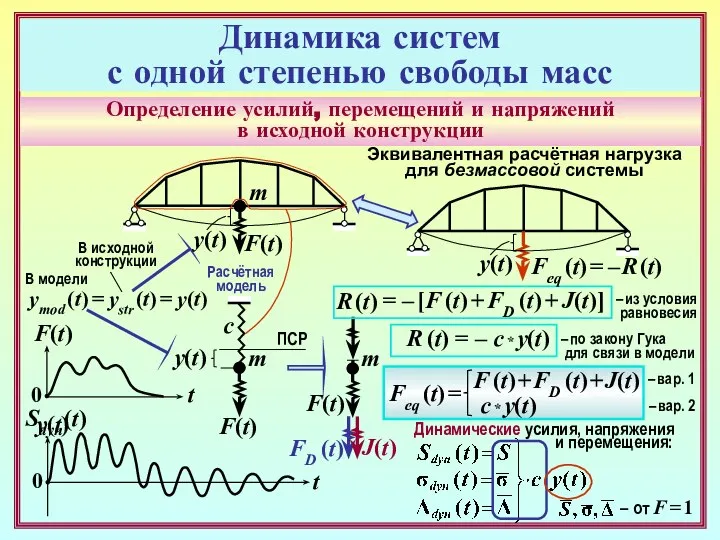
- 18. Определение усилий, перемещений и напряжений в исходной конструкции F(t) 0 t y(t) m R (t) =
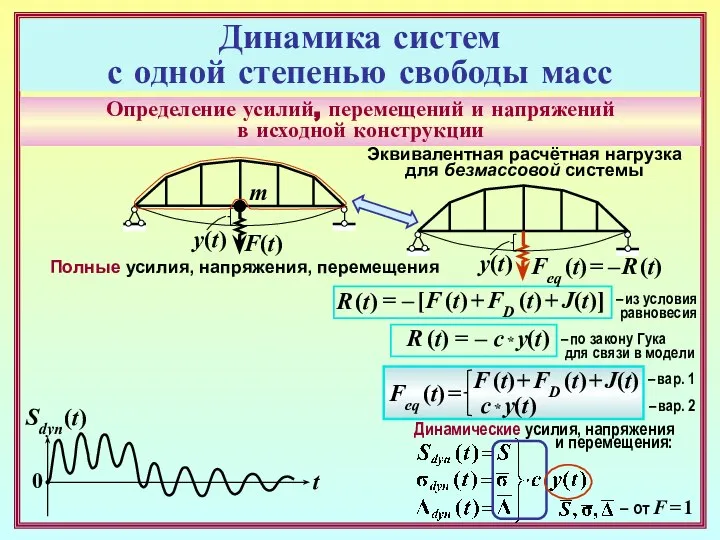
- 19. Определение усилий, перемещений и напряжений в исходной конструкции F(t) 0 t y(t) m Эквивалентная расчётная нагрузка
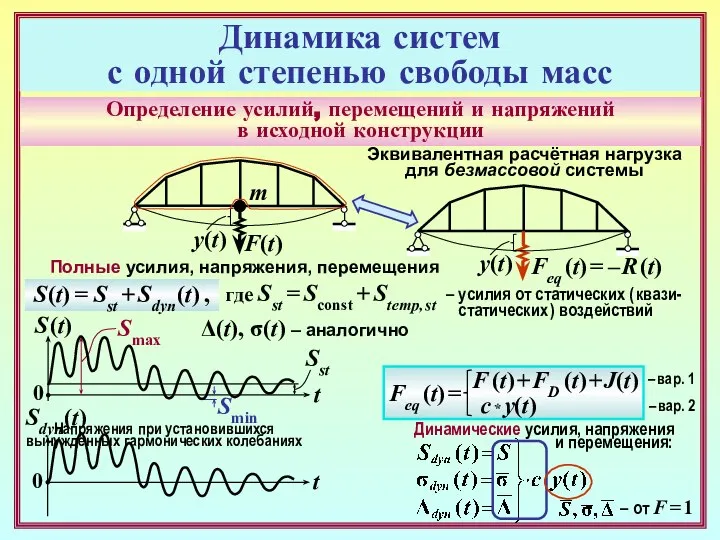
- 20. Определение усилий, перемещений и напряжений в исходной конструкции F(t) 0 t y(t) m Эквивалентная расчётная нагрузка
- 21. К о н т р о л ь н ы е в о п р о
- 23. Скачать презентацию







 Функционирующие мышцы ног при занятии вольной борьбой
Функционирующие мышцы ног при занятии вольной борьбой Замена смазки в подшипниках насоса
Замена смазки в подшипниках насоса Презентация Понятие чека
Презентация Понятие чека Эпоха Возрождения
Эпоха Возрождения fb728085_lektsiya_st1.ppt
fb728085_lektsiya_st1.ppt Концепции управления. Кибернетический подход к управлению организацией
Концепции управления. Кибернетический подход к управлению организацией COLLOQUIAL CONSTRUCTIONS
COLLOQUIAL CONSTRUCTIONS  Демократия. Народовластие
Демократия. Народовластие Культура 20 века
Культура 20 века Порядок оказания первичной медико-социальной помощи
Порядок оказания первичной медико-социальной помощи Тестирование. Программируемые цифровые устройства микроконтроллеры
Тестирование. Программируемые цифровые устройства микроконтроллеры Надпровідниковий діод
Надпровідниковий діод Презентация на тему: «таможенные платежи как инструмент регулирования перемещения молока и молочной продукции через таможенную
Презентация на тему: «таможенные платежи как инструмент регулирования перемещения молока и молочной продукции через таможенную  Презентация на тему "Методы обучения" - скачать презентации по Педагогике
Презентация на тему "Методы обучения" - скачать презентации по Педагогике Мир на Земле
Мир на Земле Итоговое сочинение
Итоговое сочинение Человек и его внутренний мир
Человек и его внутренний мир  Разработка по заказу дизайн-проекта в 3D редакторе
Разработка по заказу дизайн-проекта в 3D редакторе 7- лекция. +5-кредит Жоғары математика - копия
7- лекция. +5-кредит Жоғары математика - копия Технические правила набора
Технические правила набора Пропорция - презентация по Алгебре
Пропорция - презентация по Алгебре NS 5001. Features and Specifications
NS 5001. Features and Specifications Источник взывающего, церковь Дизайн Христа
Источник взывающего, церковь Дизайн Христа МХК
МХК Функциональные зависимости Нормализация отношений
Функциональные зависимости Нормализация отношений Развитие общей выносливости у юных лыжников- гонщиков 12-13 лет в круглогодичном периоде
Развитие общей выносливости у юных лыжников- гонщиков 12-13 лет в круглогодичном периоде Гармонизация фигуры и образа
Гармонизация фигуры и образа Кто что ест ? - презентация для начальной школы_
Кто что ест ? - презентация для начальной школы_