Содержание
- 2. 1. Определения Определение 1.1. Оператор φ n–мерного векторного пространства V называется диагонализируемым, если в V существует
- 3. 2. Нахождение собственных значений и собственных векторов линейного оператора Пусть φ – оператор n-мерного пространства V
- 4. Нахождение собственных значений и собственных векторов линейного оператора (продолжение) Получили: v – собственный вектор оператора φ
- 5. Определения 2.1. Матрица A–λI называется характеристической матрицей оператора φ (матрицы A) . Определитель характеристической матрицы, т.е.
- 6. Теорема 2.2: (Свойства подобных матриц) Пусть матрицы S и T подобны, тогда Доказательство.
- 7. Таким образом, число λ является собственным значением оператора φ тогда и только тогда, когда оно является
- 8. Пример
- 9. Пример вычисления СЗ для матрицы
- 10. 3.Свойства собственных векторов 1. Лемма 3.1. Каждый собственный вектор v оператора φ относится к единственному собственному
- 11. Лемма 3.2. Если v1 и v2 – собственные векторы оператора φ, относящиеся к одному и тому
- 12. Следствия 3.3. а) каждому собственному значению λ соответствует беско- нечное множество собственных векторов; б) если к
- 13. Лемма 3.4. Собственные векторы x1,x2,…,xk оператора φ, относящиеся к попарно различным собственным значениям λ1,λ2,…, λk ,
- 14. Точно также применим оператор φ, умножим на λ2 φ(с2 (λ2-λ1)x2…+ сk ( λk -λ1)xk) =с2λ2 (λ2-λ1)x2…+сk
- 15. Следствия 3.5: а) линейный оператор, действующий в n-мерном линейном пространстве V, не может иметь более n
- 16. Теорема 3.6. Характеристический многочлен линейного оператора не зависит от выбора базиса, то есть является инвариантом линейного
- 17. Теорема 3.8 (необходимое и достаточное условие диагональ- ности матрицы оператора) . Матрица A оператора φ в
- 18. Теорема 3.9. (Условие диагонализуемости оператора) n×n матрица A подобна диагональной т.и т.т.к. она имеет n линейно
- 19. Таким образом, и столбцы матрицы Р являются собственными векторами матрицы А (матричный линейный оператор). В силу
- 20. Таким образом, Получили А так как Р - невырожденная матрица, то - диагональная матрица. QED
- 21. Критерий диагонализируемости оператора: оператор φ диагонализируем тогда и только тогда, когда в пространстве V существует базис,
- 22. Пример
- 23. Пример (продолжение)
- 25. 4.Линейный оператор с простым спектром Определение 4.1 Набор всех собственных значений оператора называется спектром оператора. Определение
- 26. Пример: матрица является матрицей оператора с простым спектром
- 28. Скачать презентацию




















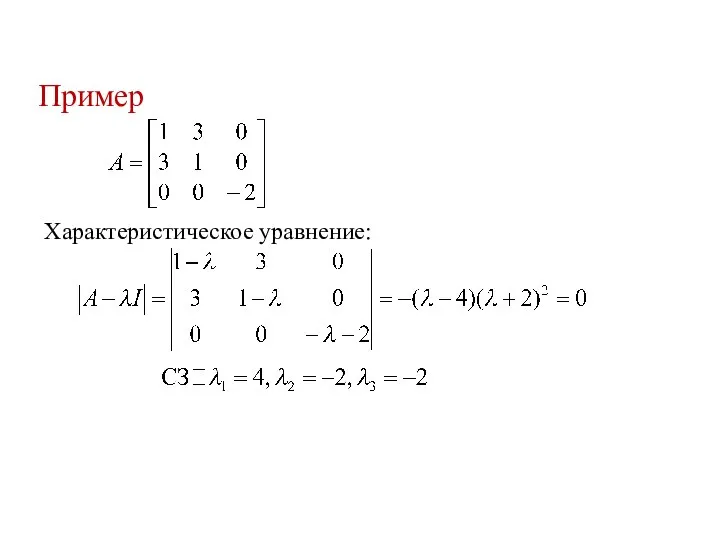




 Древние дороги и знаменитые торговые пути
Древние дороги и знаменитые торговые пути Багато функціональна похило - скерована бурова установка призначена для буріння різного типу свердловин
Багато функціональна похило - скерована бурова установка призначена для буріння різного типу свердловин Балансовый метод исследования в Зарубежном туристском страноведении
Балансовый метод исследования в Зарубежном туристском страноведении Pascal Указатели Динамические переменные
Pascal Указатели Динамические переменные  Атқарушы механизмдер және реттеуші органдар
Атқарушы механизмдер және реттеуші органдар Качество - это образ жизни. Качество продукции компании APPLE
Качество - это образ жизни. Качество продукции компании APPLE Транспорт. Урок ИЗО
Транспорт. Урок ИЗО Древесина. Строение древесины
Древесина. Строение древесины Летние Олимпийские игры
Летние Олимпийские игры Тем.3.Зан.2.мод.ppt
Тем.3.Зан.2.мод.ppt Презентация на тему "Индивидуальный подбор контрацептивов в зависимости от возраста" - скачать презентации по Медицине
Презентация на тему "Индивидуальный подбор контрацептивов в зависимости от возраста" - скачать презентации по Медицине Планирование, построение, контроль и управление учебно-тренировочным процессом
Планирование, построение, контроль и управление учебно-тренировочным процессом Библейские сюжеты в произведениях христианской православной культуры
Библейские сюжеты в произведениях христианской православной культуры Начало жизни. Кукла «Пасхальная голубка»
Начало жизни. Кукла «Пасхальная голубка» Бизнес-план по составлению бизнес-планов
Бизнес-план по составлению бизнес-планов Синус, косинус, тангенс и котангенс. Алгебра и начала анализа, 10 класс
Синус, косинус, тангенс и котангенс. Алгебра и начала анализа, 10 класс Основания по химии
Основания по химии Непосредственная и представительная демократия. Особенности федерализма в России. (Тема 4)
Непосредственная и представительная демократия. Особенности федерализма в России. (Тема 4) Лекция 2. Теория профилактики ХНИЗ
Лекция 2. Теория профилактики ХНИЗ Базовые механизмы каракури. Основные элементы малой механизации
Базовые механизмы каракури. Основные элементы малой механизации Unforgettable tour to Czech Republic
Unforgettable tour to Czech Republic Кладка простенка с четвертями толщиной 510 мм
Кладка простенка с четвертями толщиной 510 мм Hamburg 2016
Hamburg 2016 Семинар – практикум для учителей Взаимодействие в работе логопеда и учителя. Проблема дисграфии. Учитель-логопед ГОУ СОШ 1688 г.
Семинар – практикум для учителей Взаимодействие в работе логопеда и учителя. Проблема дисграфии. Учитель-логопед ГОУ СОШ 1688 г.  КТ Бадминтон
КТ Бадминтон Анализ затрат на лекарственные средства с помощью ABC/VEV методологии
Анализ затрат на лекарственные средства с помощью ABC/VEV методологии  Гипоксия плода и асфиксия новорожденного
Гипоксия плода и асфиксия новорожденного Карл Павлович Брюллов 1799 - 1852 Презентация к внеклассному занятию по теме: «Картинная галерея» учителя начальных классов ГСОШ№7 К
Карл Павлович Брюллов 1799 - 1852 Презентация к внеклассному занятию по теме: «Картинная галерея» учителя начальных классов ГСОШ№7 К