Содержание
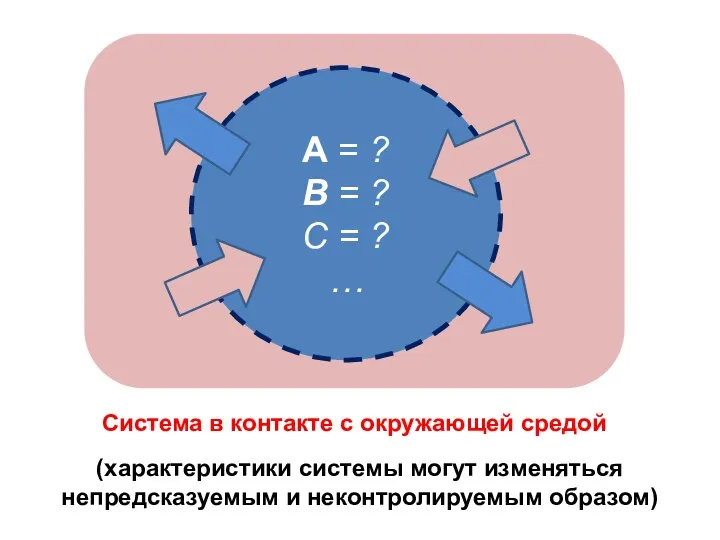
- 2. (характеристики системы могут изменяться непредсказуемым и неконтролируемым образом)
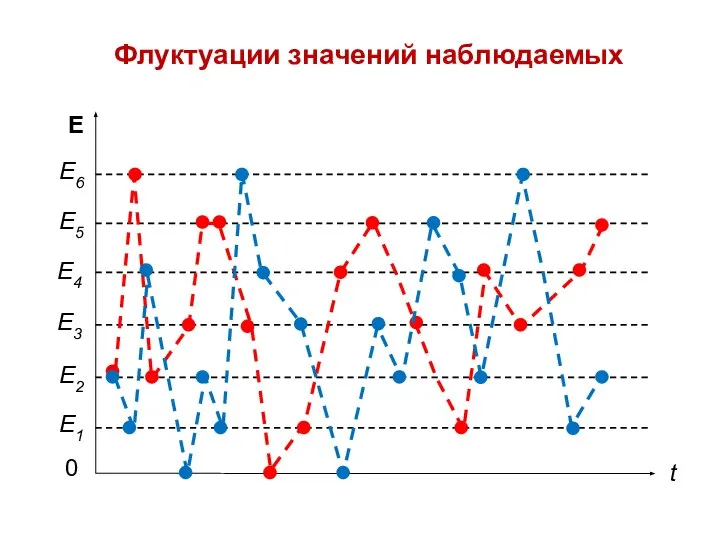
- 3. Флуктуации значений наблюдаемых
- 4. Чему равно значение энергии частицы, способной взаимодействовать с окружающей средой? Е = ??? Такой вопрос является
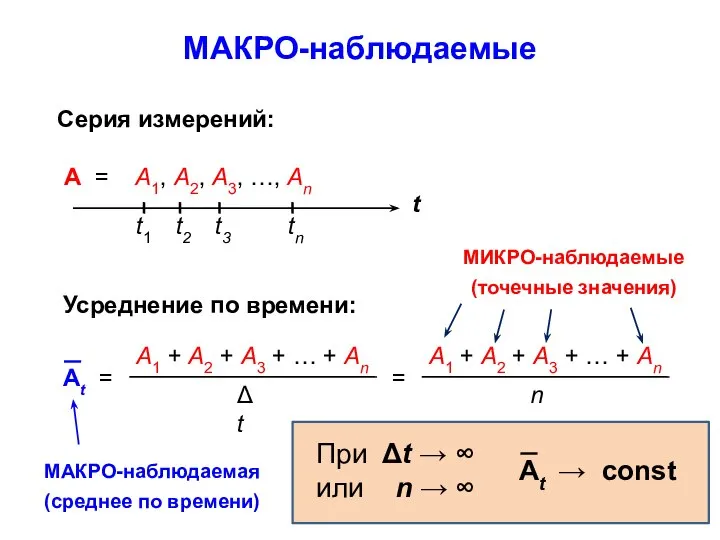
- 5. СИСТЕМЫ МИКРО-наблюдаемые МАКРО-наблюдаемые
- 6. МАКРО-наблюдаемые Усреднение по времени:
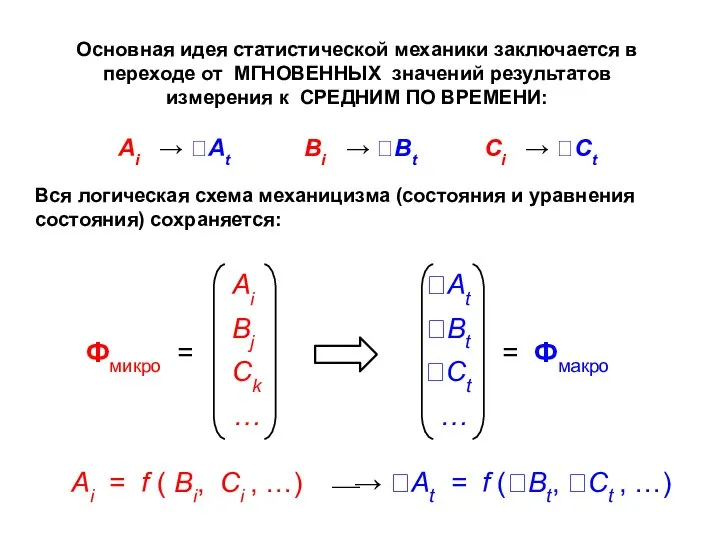
- 7. Основная идея статистической механики заключается в переходе от МГНОВЕННЫХ значений результатов измерения к СРЕДНИМ ПО ВРЕМЕНИ:
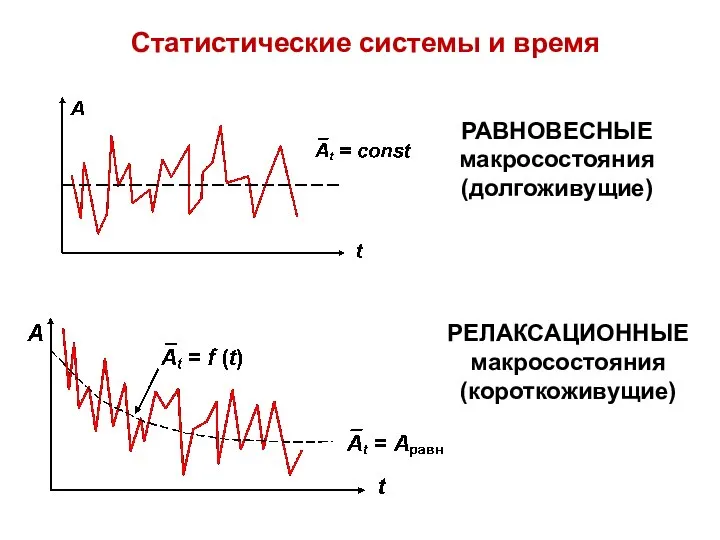
- 8. РАВНОВЕСНЫЕ макросостояния (долгоживущие) РЕЛАКСАЦИОННЫЕ макросостояния (короткоживущие) Статистические системы и время
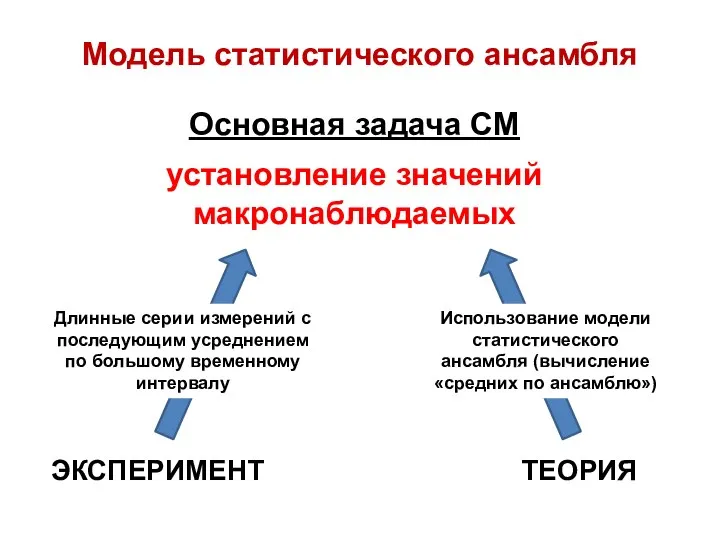
- 9. Модель статистического ансамбля Основная задача СМ установление значений макронаблюдаемых Длинные серии измерений с последующим усреднением по
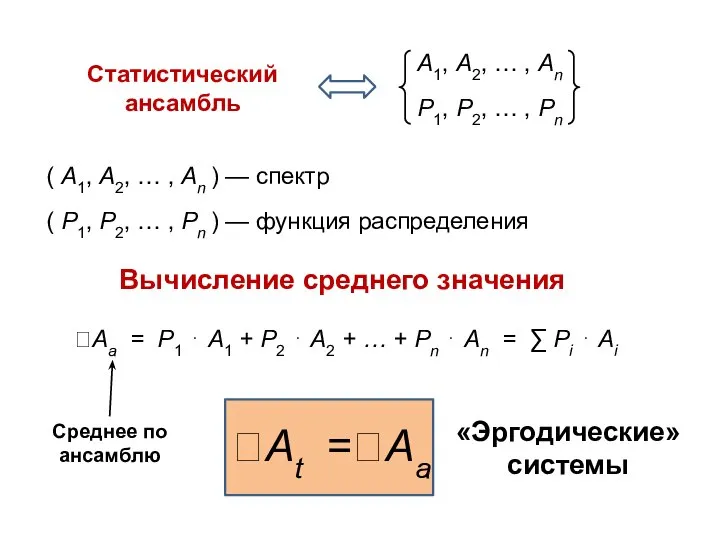
- 11. Вычисление среднего значения «Эргодические» системы
- 12. Определение спектра Определение вероятностей априорные модели Постулат: игральная кость симметрична и, следовательно, все вероятности одинаковы Aa
- 13. Априорные модели функций распределения МИКРОКАНОНИЧЕСКИЙ ансамбль (МКА) (энергия) E = const; (число частиц) N = const
- 14. Микроканонический ансамбль Функция распределения МКА Р1 = Р2 = … = Рn = 1/Ω где Ω
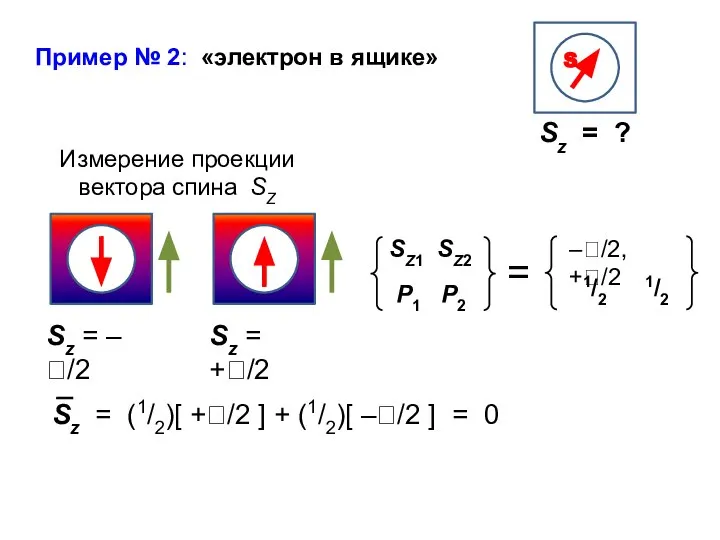
- 15. Пример № 2: «электрон в ящике» Измерение проекции вектора спина SZ
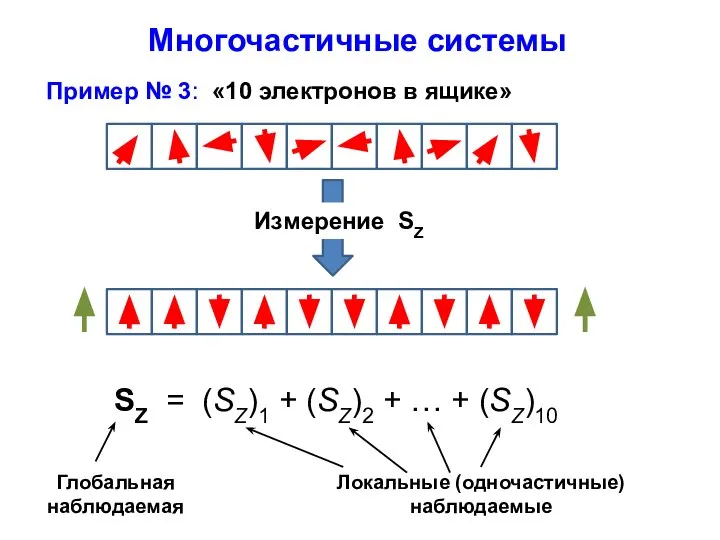
- 16. Многочастичные системы Пример № 3: «10 электронов в ящике» SZ = (SZ)1 + (SZ)2 + …
- 17. Глобальные и локальные наблюдаемые Глобальная проекция SZ / { –5 –4 –3 –2 –1 0
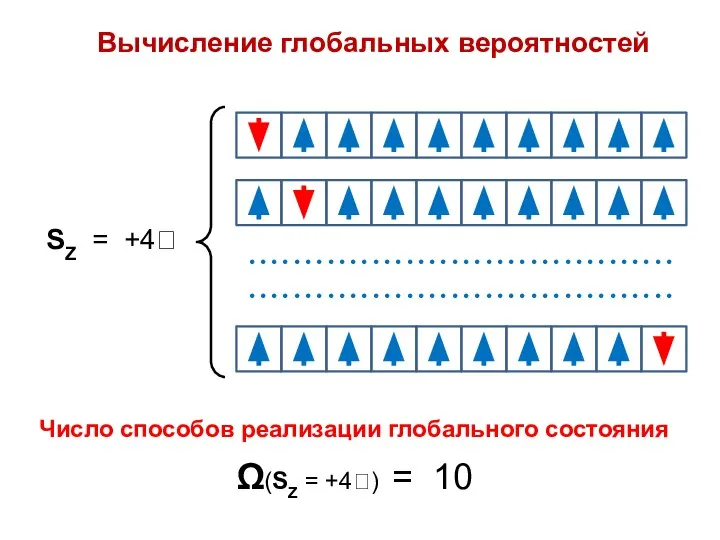
- 18. Вычисление глобальных вероятностей SZ = +4 Число способов реализации глобального состояния Ω(SZ = +4) = 10
- 19. Глобальные вероятности: Pi глоб. = Ωi / 1024 Число ЛОКАЛЬНЫХ состояний (различимых «изнутри») Ω = ∑
- 20. Si — термодинамическая энтропия, k = 1,38⋅10–23 Дж/моль⋅К — постоянная Больцмана Ωi → ln Ωi =
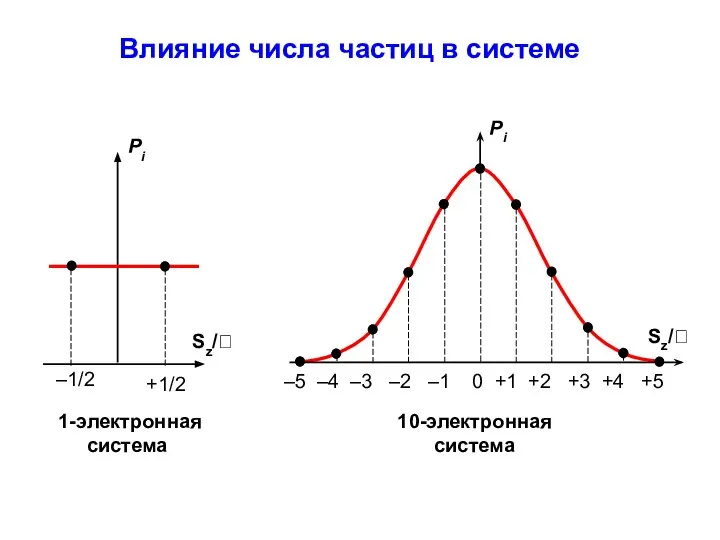
- 21. Влияние числа частиц в системе
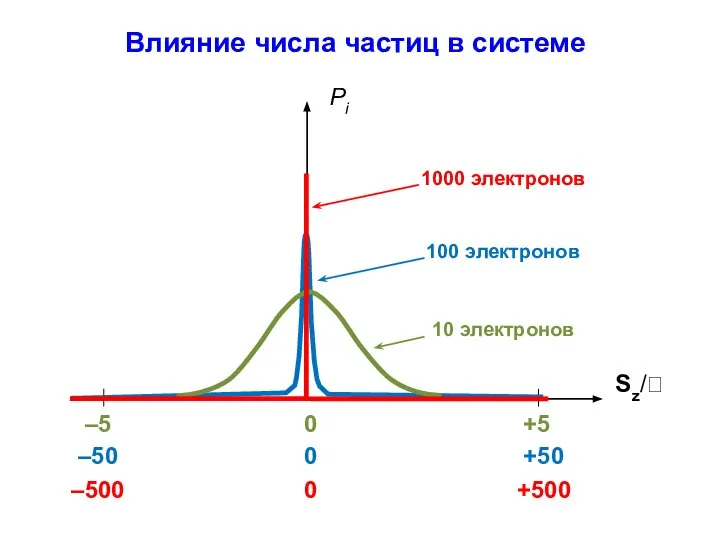
- 22. Влияние числа частиц в системе
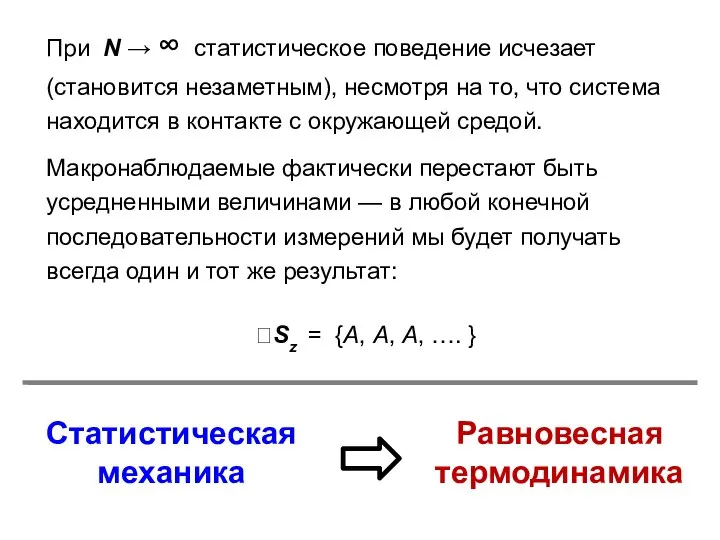
- 23. При N → ∞ статистическое поведение исчезает (становится незаметным), несмотря на то, что система находится в
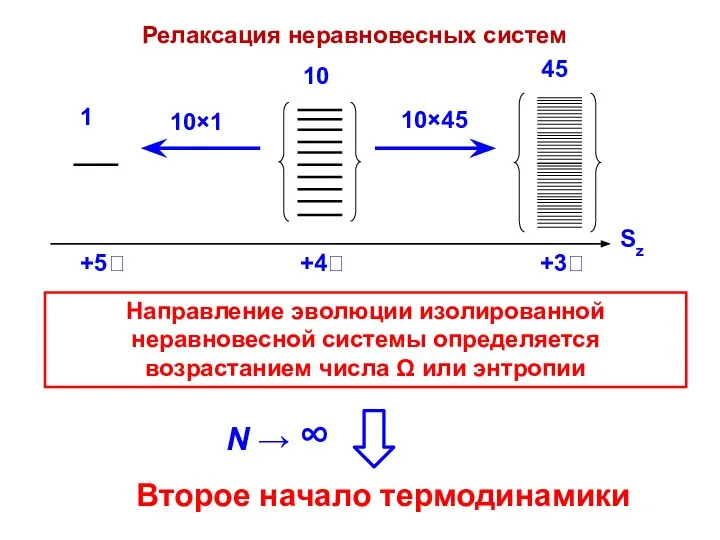
- 24. Направление эволюции изолированной неравновесной системы определяется возрастанием числа Ω или энтропии Релаксация неравновесных систем
- 25. Второе начало термодинамики а) Все самопроизвольные процессы в изолированных системах сопровождаются возрастанием энтропии; процессы с уменьшением
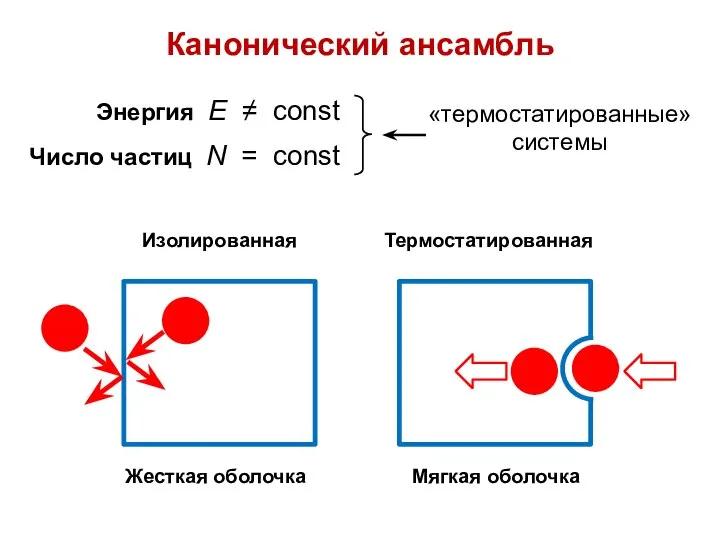
- 26. Канонический ансамбль
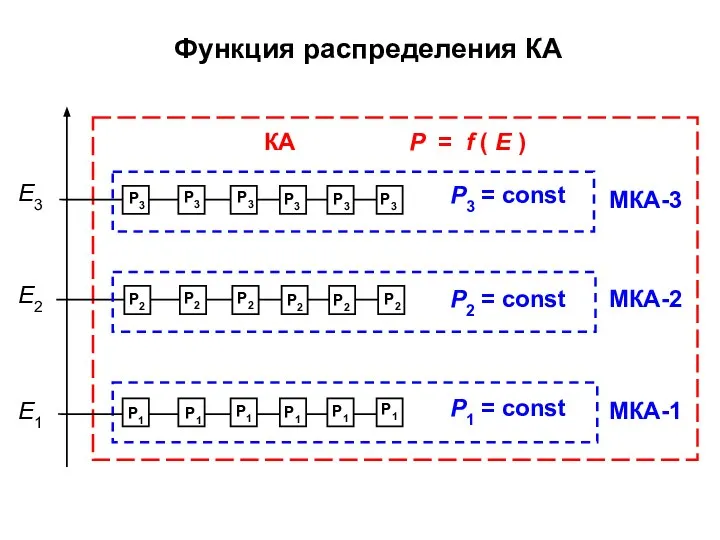
- 28. Функция распределения КА
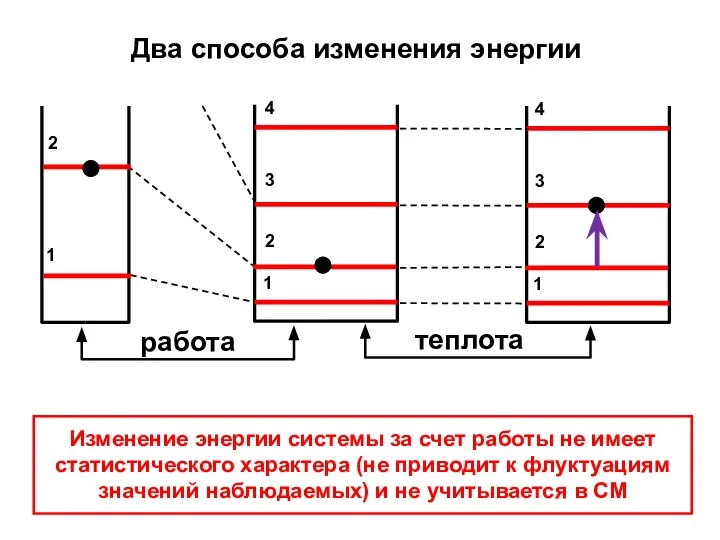
- 29. Два способа изменения энергии Изменение энергии системы за счет работы не имеет статистического характера (не приводит
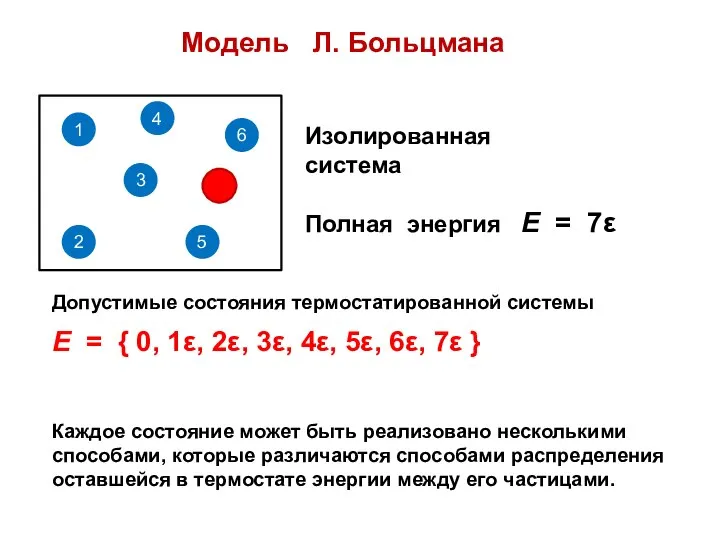
- 30. Модель Л. Больцмана Е = { 0, 1ε, 2ε, 3ε, 4ε, 5ε, 6ε, 7ε } Допустимые
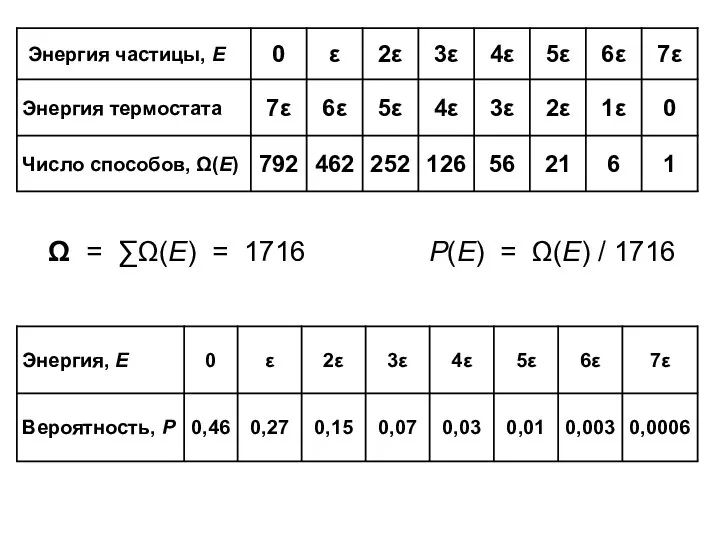
- 31. Ω = ∑Ω(Е) = 1716 Р(Е) = Ω(Е) / 1716
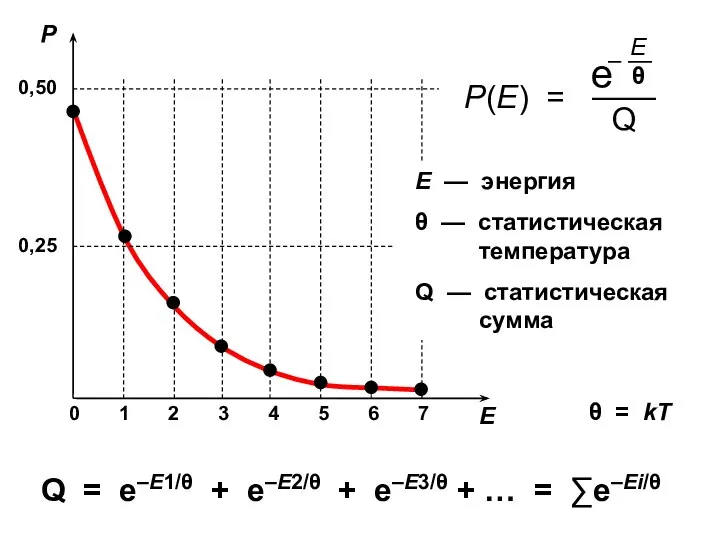
- 32. Q = е–Е1/θ + е–Е2/θ + е–Е3/θ + … = ∑е–Еi/θ E — энергия θ —
- 33. Числовые значения больцмановских факторов е–Еi/θ и статистической суммы Q зависят от калибровки шкалы энергии. Вероятности Pi
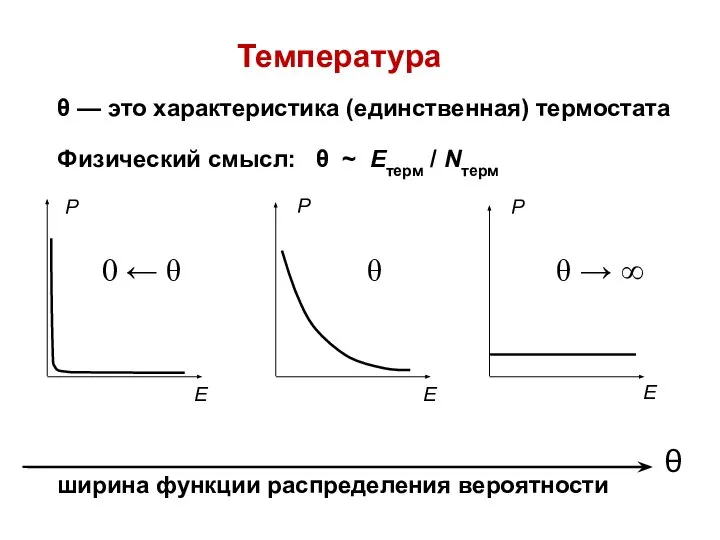
- 34. Температура
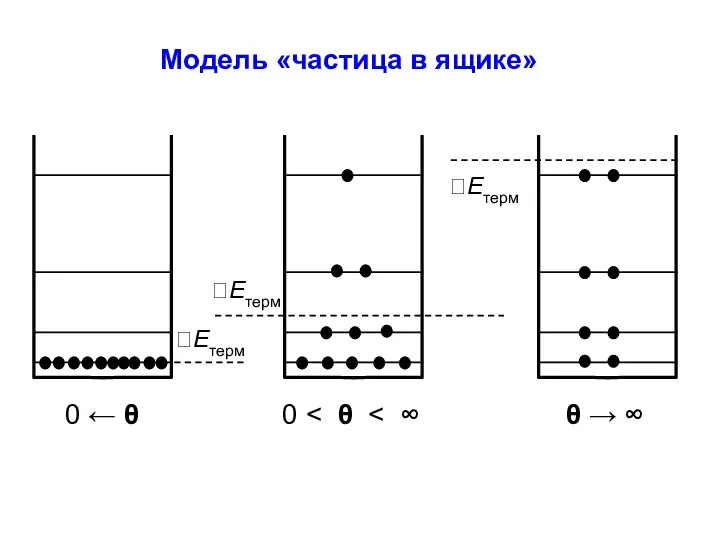
- 35. Модель «частица в ящике»
- 36. Модель «частица в ящике»
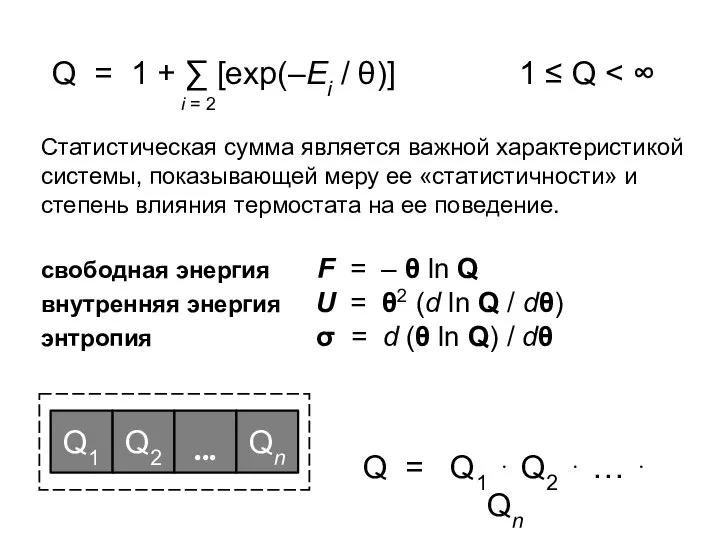
- 37. Статистическая сумма Еi = R ⋅ (n2 – 1) Соглашение: при вычислении статистических сумм следует пользоваться
- 38. 1 ≤ Q Статистическая сумма является важной характеристикой системы, показывающей меру ее «статистичности» и степень влияния
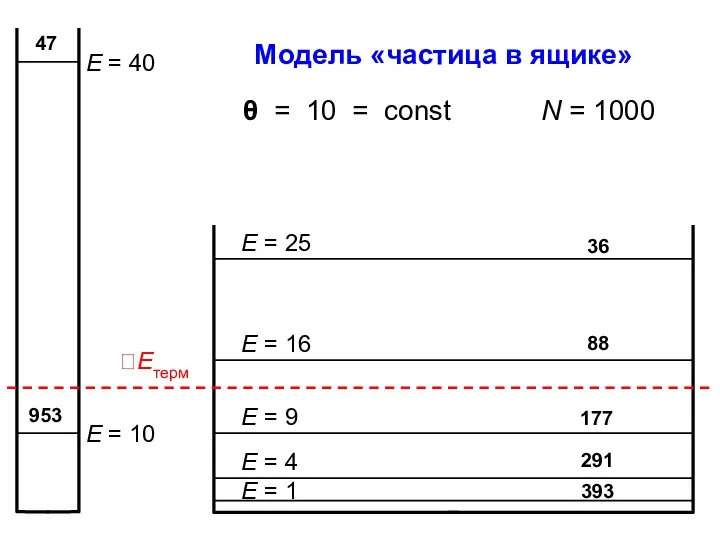
- 39. Модель «частица в ящике» Q = 2,54 Q = 1,05
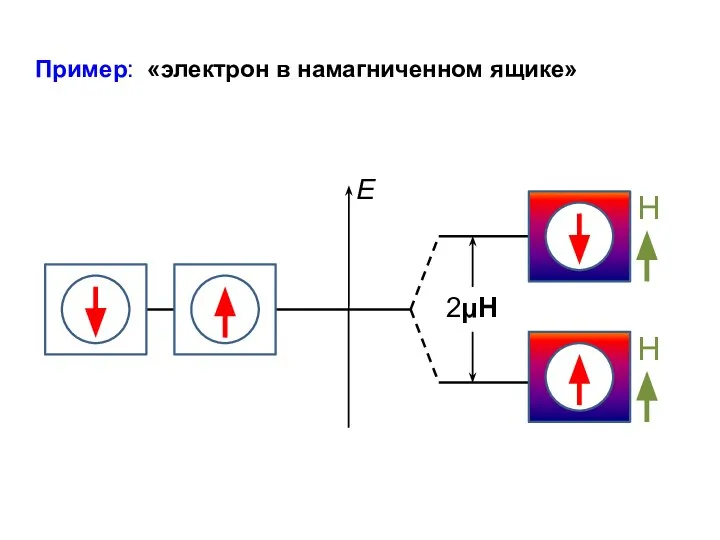
- 40. Пример: «электрон в намагниченном ящике»
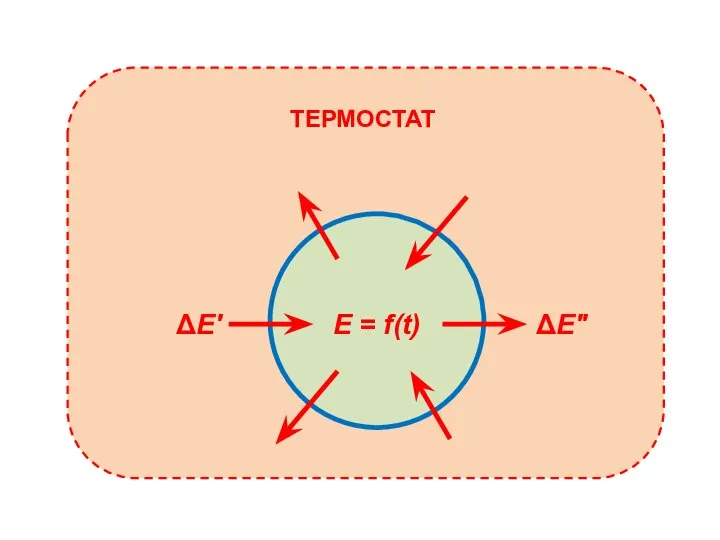
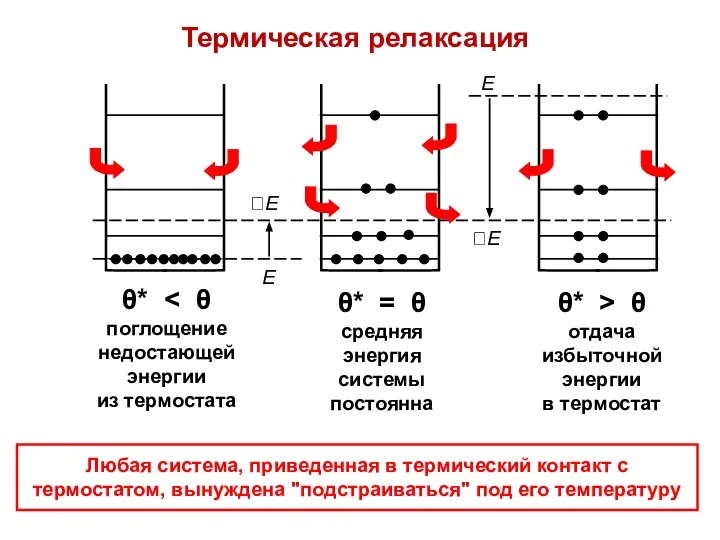
- 42. Термическая релаксация Любая система, приведенная в термический контакт с термостатом, вынуждена "подстраиваться" под его температуру
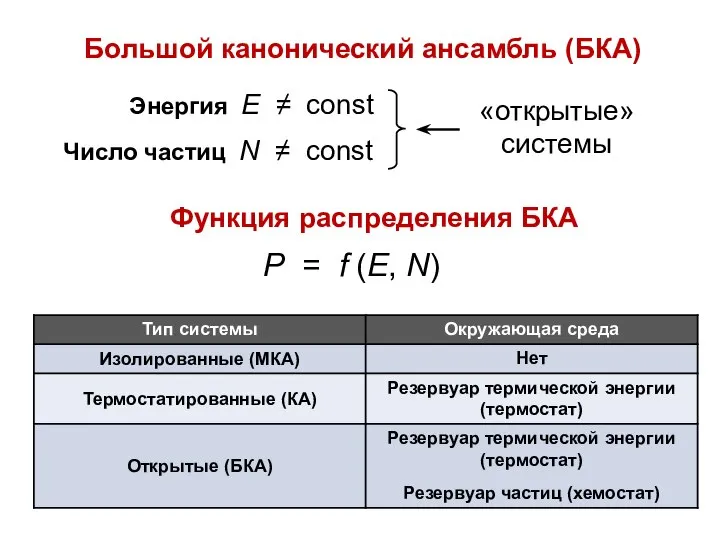
- 43. Большой канонический ансамбль (БКА) Функция распределения БКА Р = f (E, N)
- 45. КА № 0 КА № 1 КА № 2 КА № 3 Пример: «Намагниченный ящик в
- 46. P = f (E, N1, N2, … , Nn) = = (1/Z) ⋅ exp[–(E – μ1⋅N1
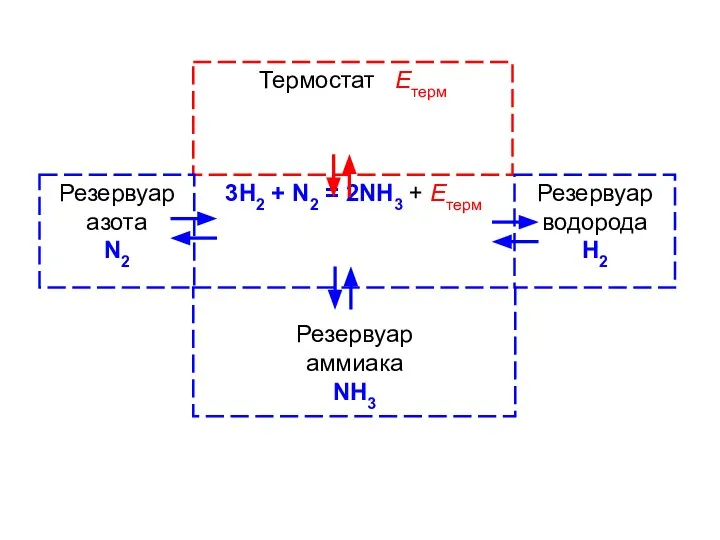
- 47. Химический потенциал ХЕМОСТАТ — резервуар ХИМИЧЕСКОЙ энергии (потенциальной энергии частиц хемостата) ХИМИЧЕСКИЙ ПОТЕНЦИАЛ — средняя химическая
- 48. Химическая энергия Частицы одного сорта (одинаковой химической природы), вынужденные находиться в одном и том же объеме
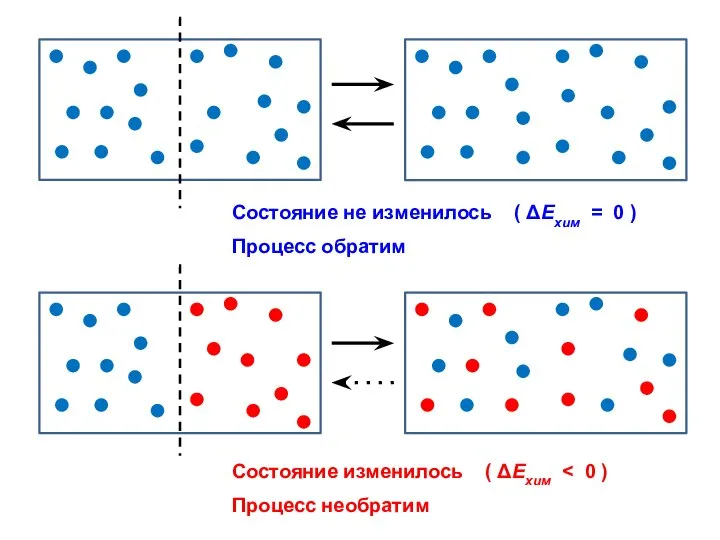
- 49. Состояние не изменилось ( ΔΕхим = 0 ) Состояние изменилось ( ΔΕхим Процесс обратим Процесс необратим
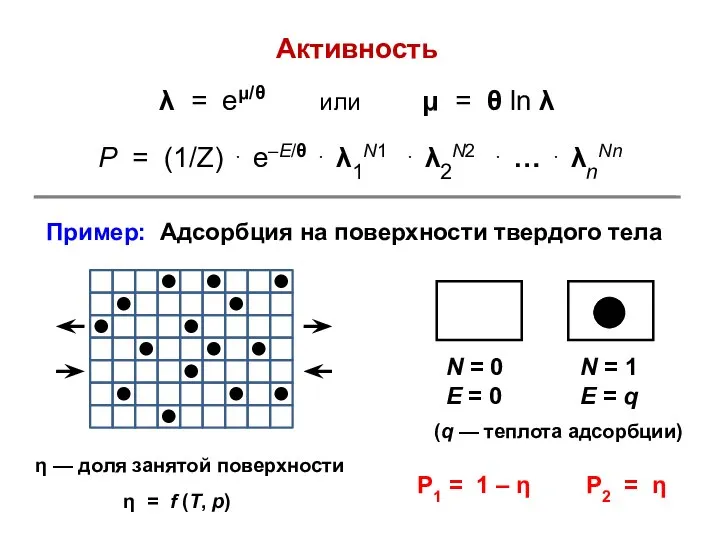
- 50. Активность λ = eμ/θ или μ = θ ln λ P = (1/Z) ⋅ e–Е/θ ⋅
- 51. Вероятности обнаружения системы в свободном (1) и занятом (2) состояниях: P1 = 1/Z и P2 =
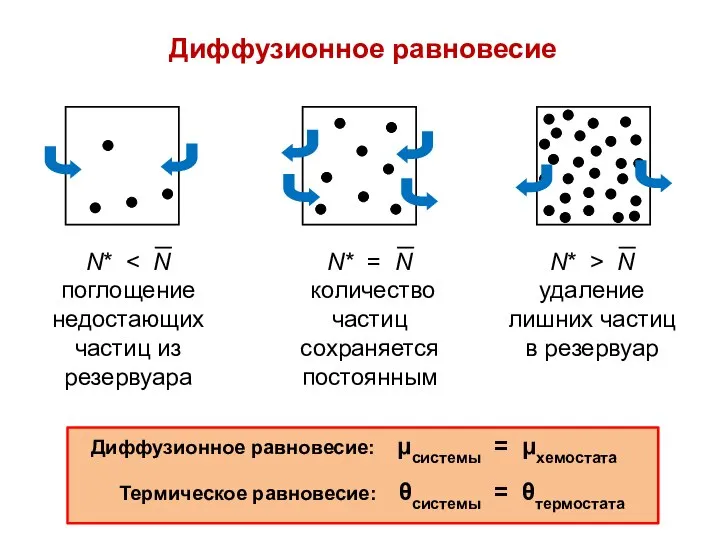
- 52. Диффузионное равновесие Диффузионное равновесие: μсистемы = μхемостата Термическое равновесие: θсистемы = θтермостата
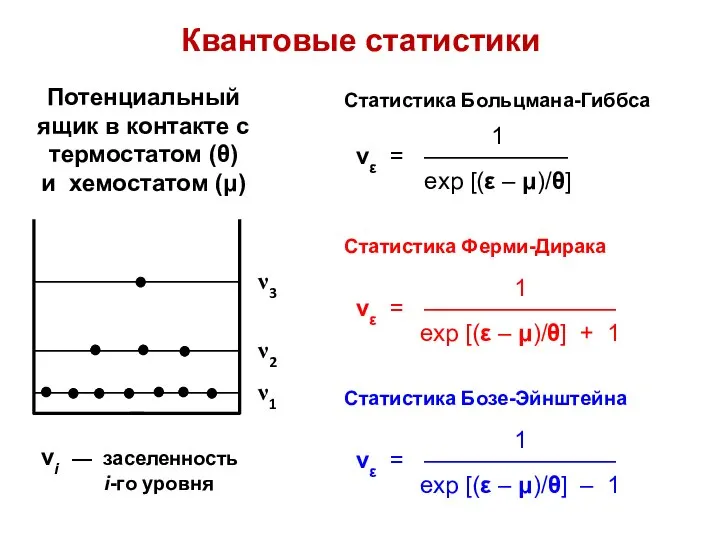
- 53. Квантовые статистики
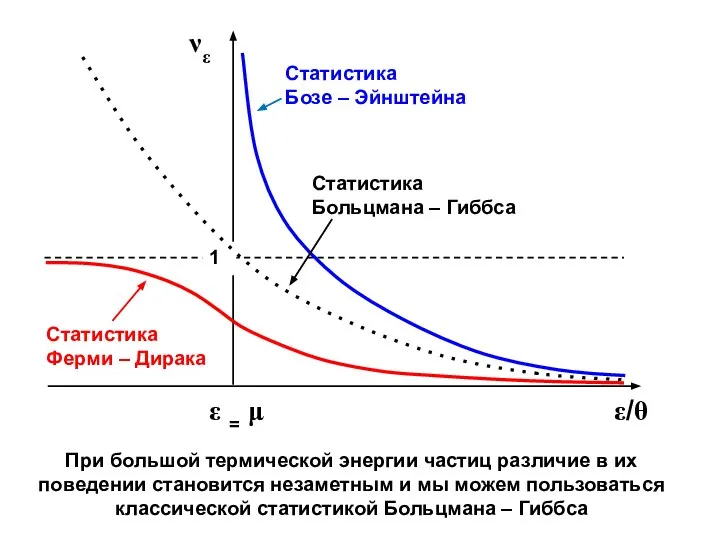
- 54. При большой термической энергии частиц различие в их поведении становится незаметным и мы можем пользоваться классической
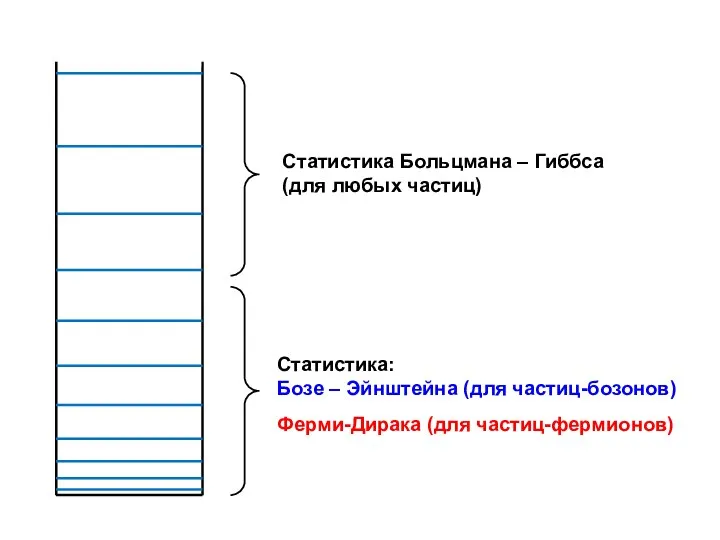
- 55. Статистика Больцмана – Гиббса (для любых частиц) Статистика: Бозе – Эйнштейна (для частиц-бозонов) Ферми-Дирака (для частиц-фермионов)
- 57. Скачать презентацию



















 Культура России во второй половине ХIX века
Культура России во второй половине ХIX века MVC and MVP. References
MVC and MVP. References Дыхание - 2
Дыхание - 2 Спин элементарных частиц
Спин элементарных частиц  Организация уроков лыжной подготовки в школе
Организация уроков лыжной подготовки в школе Бетон для железобетонных конструкций
Бетон для железобетонных конструкций Управление становлением образовательных практик_Москва
Управление становлением образовательных практик_Москва Специфика сервисной деятельности как науки
Специфика сервисной деятельности как науки Китайский для начинающих. Правила каллиграфии
Китайский для начинающих. Правила каллиграфии Экономические ресурсы предприятия Учебные вопросы: Имущество и капитал предприятия. Экономическая сущность, состав и структура
Экономические ресурсы предприятия Учебные вопросы: Имущество и капитал предприятия. Экономическая сущность, состав и структура АРХИТЕКТУРА Архитектура г. Омска Приложение к хрестоматии «Музыка, театр, изобразительное искусство Омского Прииртышья»
АРХИТЕКТУРА Архитектура г. Омска Приложение к хрестоматии «Музыка, театр, изобразительное искусство Омского Прииртышья» Ойын алаңы.Теориялық механика
Ойын алаңы.Теориялық механика Геометрия в работах Эшера.
Геометрия в работах Эшера.  Обработка совместных измерений
Обработка совместных измерений  Балет
Балет Кто что ест ? - презентация для начальной школы_
Кто что ест ? - презентация для начальной школы_ Урок №11 Вычислительные умения и навыки Сравнение длин отрезков. Величины
Урок №11 Вычислительные умения и навыки Сравнение длин отрезков. Величины  Подготовка к обслуживанию. Подготовка посуды, приборов, столов
Подготовка к обслуживанию. Подготовка посуды, приборов, столов Преобразование типов
Преобразование типов Перспектива Обратная перспектива
Перспектива Обратная перспектива Презентация "Урок-экскурсия по картине Н.П. Богданова-Бельского "Устный счет"" - скачать презентации по МХК
Презентация "Урок-экскурсия по картине Н.П. Богданова-Бельского "Устный счет"" - скачать презентации по МХК Статистические распределения
Статистические распределения Конструкция автомобиля. Сцепление
Конструкция автомобиля. Сцепление Анатомия как наука и предмет
Анатомия как наука и предмет Середовища програмування
Середовища програмування MorphOS 1.4
MorphOS 1.4 Художественная культура античности. Древний Рим
Художественная культура античности. Древний Рим Презентация по ОБЖ Осторожно, тонкий лед ! Урок ОБЖ, 7 класс.
Презентация по ОБЖ Осторожно, тонкий лед ! Урок ОБЖ, 7 класс.