Содержание
- 2. Сортировка 4 2 Нижняя граница задачи сортировки Вопрос: существует ли алгоритм сортировки, основанный на сравнениях и
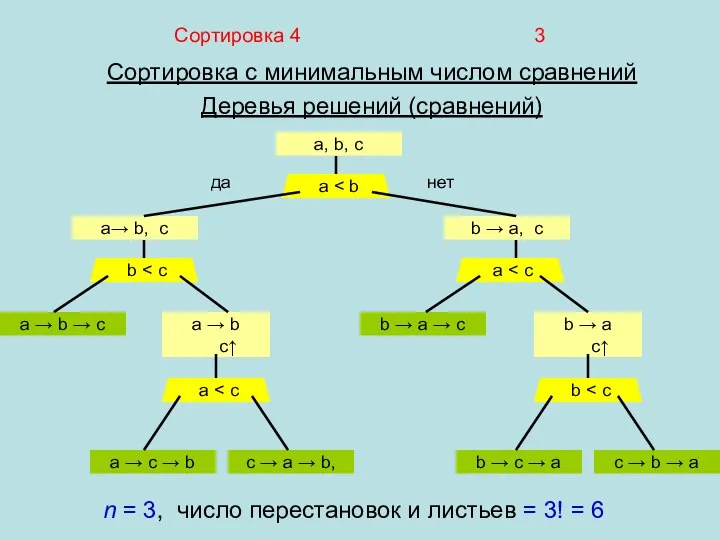
- 3. Сортировка 4 3 Сортировка с минимальным числом сравнений Деревья решений (сравнений) a, b, c a→ b,
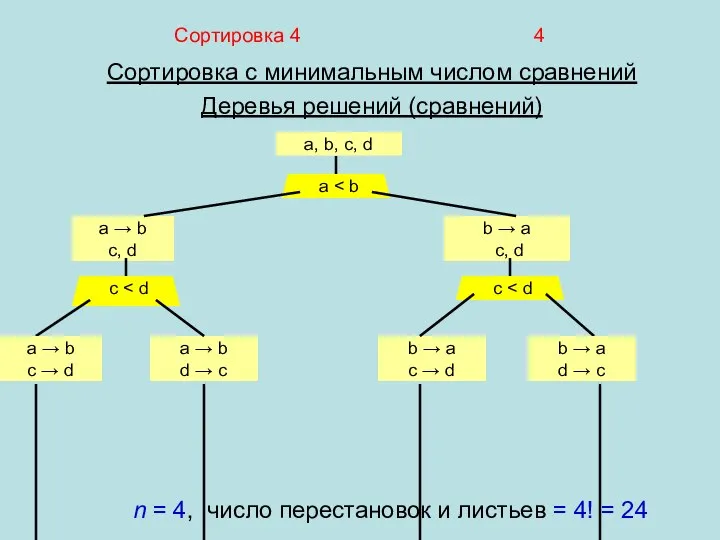
- 4. Сортировка 4 4 Сортировка с минимальным числом сравнений Деревья решений (сравнений) a, b, c, d a
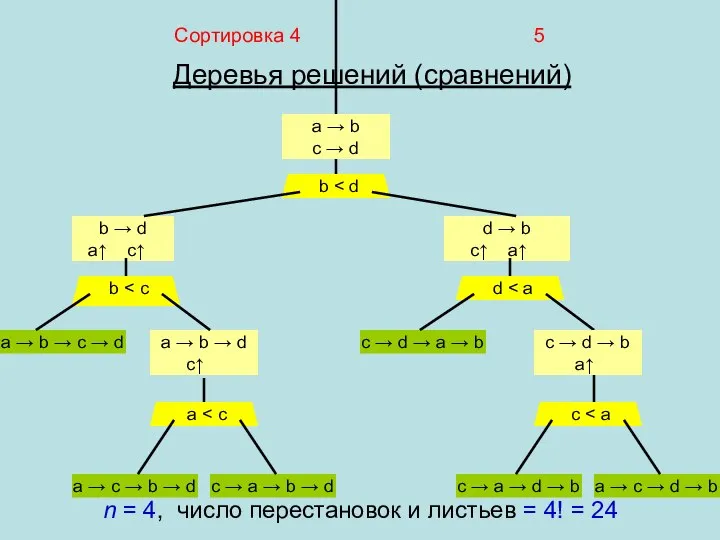
- 5. Сортировка 4 5 Деревья решений (сравнений) b → d a↑ c↑ d → b c↑ a↑
- 6. Сортировка 4 6 Деревья решений (сравнений) Пусть m высота дерева (максимальное число сравнений). 2m ≥ число
- 7. Сортировка 4 7 Формула Стирлинга ⎡log2 n!⎤ ≤ log2 n! + 1 ⎡log2 n!⎤ = n
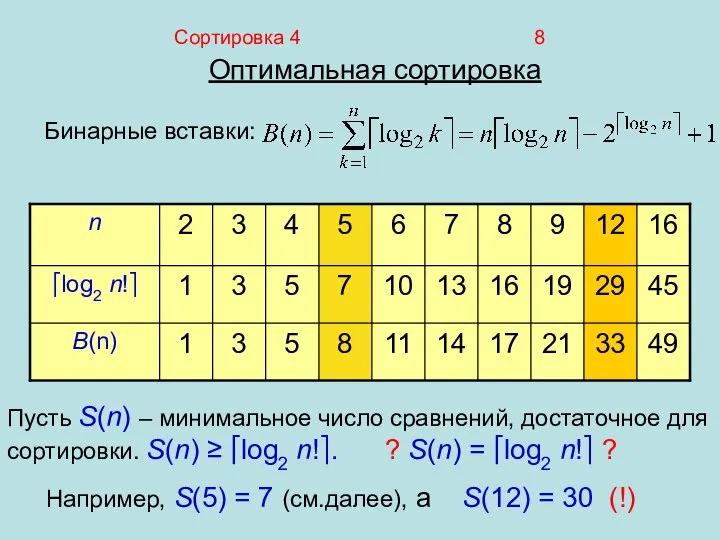
- 8. Сортировка 4 8 Оптимальная сортировка Бинарные вставки: Пусть S(n) – минимальное число сравнений, достаточное для сортировки.
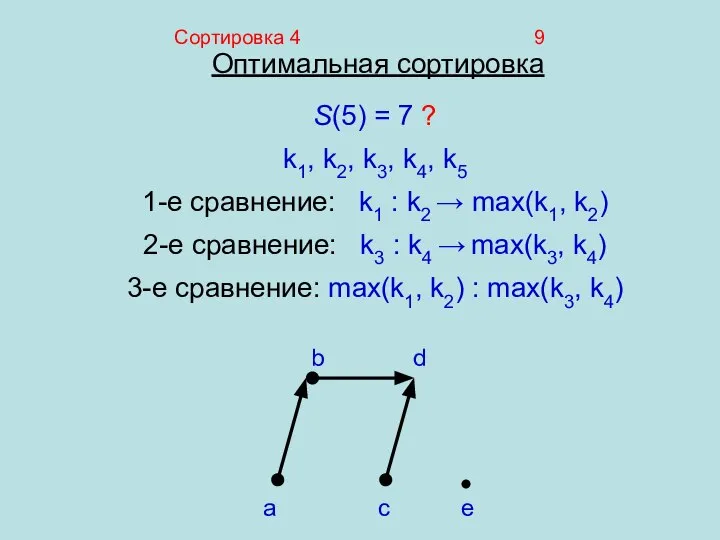
- 9. Сортировка 4 9 Оптимальная сортировка S(5) = 7 ? k1, k2, k3, k4, k5 1-е сравнение:
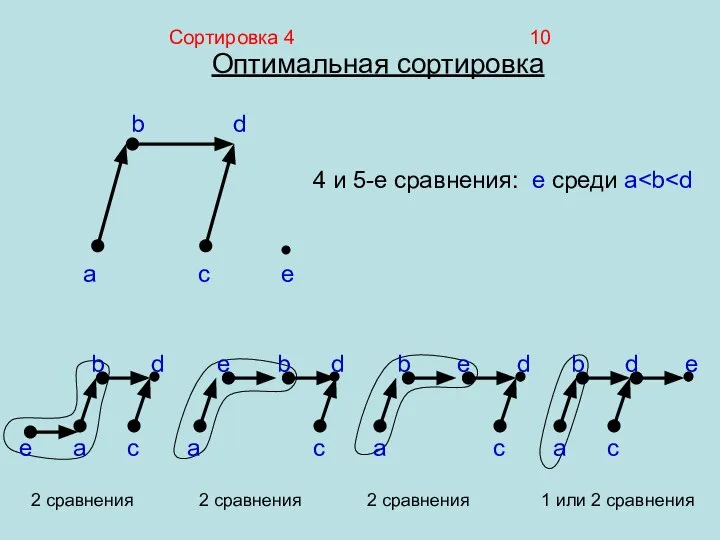
- 10. Сортировка 4 10 Оптимальная сортировка 4 и 5-е сравнения: e среди a e a a a
- 11. Сортировка 4 11 Поразрядная сортировка (Распределяющая сортировка) Пример 1 (с картами). Карта = (масть, достоинство) Масть:
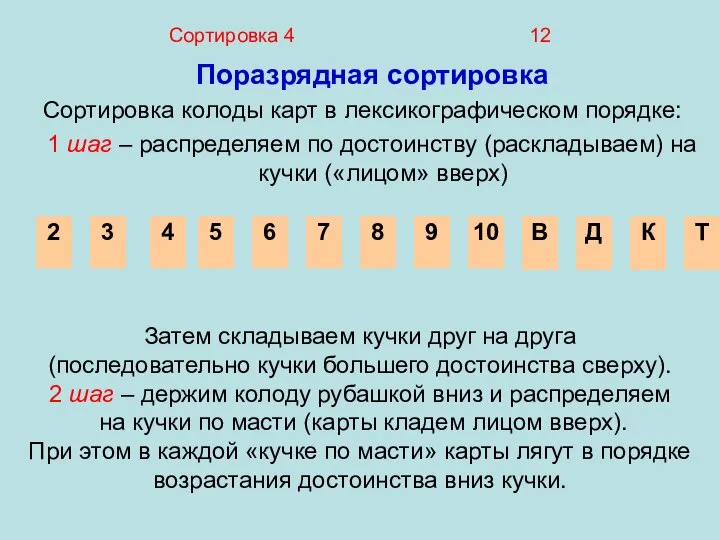
- 12. Сортировка 4 12 Поразрядная сортировка Сортировка колоды карт в лексикографическом порядке: 1 шаг – распределяем по
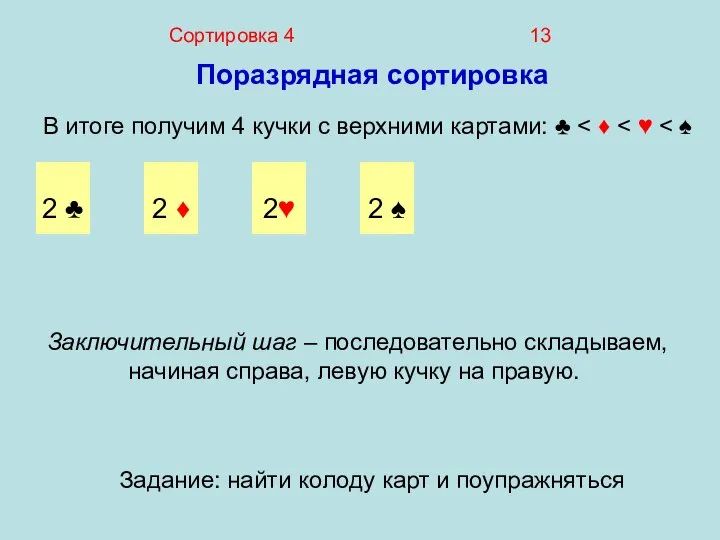
- 13. Сортировка 4 13 Поразрядная сортировка В итоге получим 4 кучки с верхними картами: ♣ 2 ♣
- 14. Сортировка 4 14 Поразрядная сортировка Пример 2 (с числами). Рассмотрим целые (положительные) трехразрядные числа в позиционной
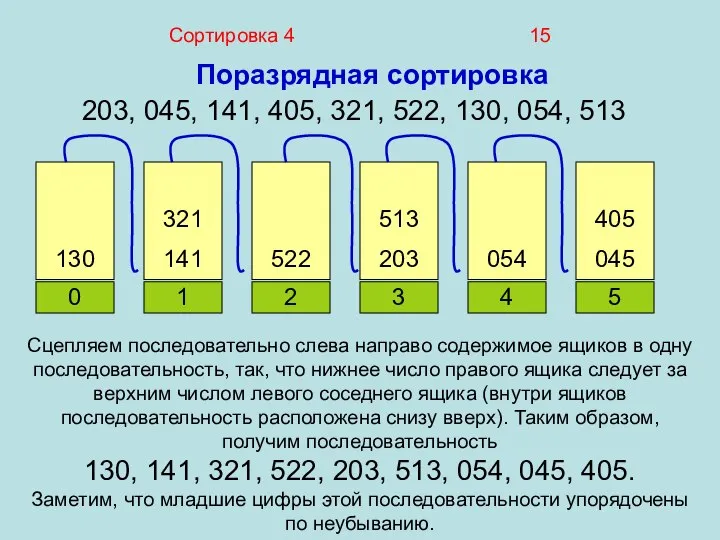
- 15. Сортировка 4 15 Поразрядная сортировка 203, 045, 141, 405, 321, 522, 130, 054, 513 Сцепляем последовательно
- 16. Сортировка 4 16 Поразрядная сортировка 130, 141, 321, 522, 203, 513, 054, 045, 405 2 шаг
- 17. Сортировка 4 17 Поразрядная сортировка 203, 405, 513, 321, 522, 130, 141, 045, 054 3 шаг
- 18. Сортировка 4 18 Алгоритм поразрядной сортировки В общем случае даны числа (ключи): x1, x2, x3,…, xn.
- 19. Сортировка 4 19 Алгоритм поразрядной сортировки Для представления «ящиков» и их сцепления в новую последовательность используем
- 20. Сортировка 4 20 Алгоритм поразрядной сортировки Алгоритм: Create(Q); Create(q[*]); for j := 1 to p do
- 21. Сортировка 4 21 Алгоритм поразрядной сортировки Подсчитаем количество операций. Внешний цикл по разрядам выполняется p раз.
- 23. Скачать презентацию









![Сортировка 4 20 Алгоритм поразрядной сортировки Алгоритм: Create(Q); Create(q[*]); for j](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301817/slide-19.jpg)

 Десятичные дроби. Их чтение и запись - презентация по Алгебре
Десятичные дроби. Их чтение и запись - презентация по Алгебре Требования к реферату
Требования к реферату Работа с файлами
Работа с файлами Делегаты, события, анонимные методы
Делегаты, события, анонимные методы Место и роль науки о культуре в системе современного гуманитарного знания
Место и роль науки о культуре в системе современного гуманитарного знания ТЕМА: "ОЦЕНКА ПЕРСОНАЛА: ДАЕШЬ ЭФФЕКТИВНОСТЬ!? Реализация оценки в компании "ВОЛЯ" с численностью более 1800 человек"
ТЕМА: "ОЦЕНКА ПЕРСОНАЛА: ДАЕШЬ ЭФФЕКТИВНОСТЬ!? Реализация оценки в компании "ВОЛЯ" с численностью более 1800 человек"  Диалектизмы родного села
Диалектизмы родного села Тенденции 1960-х годов
Тенденции 1960-х годов «Дари добро» Социальный проект .
«Дари добро» Социальный проект . виды и характеристики логистических систем
виды и характеристики логистических систем  Развивающиеся страны Около 140 государств Азии, Африки, Латинской Америки и Океании. Страны – лидеры развивающегося мира (НИС, О
Развивающиеся страны Около 140 государств Азии, Африки, Латинской Америки и Океании. Страны – лидеры развивающегося мира (НИС, О Система права
Система права Содержание логопедической работы по формированию самоконтроля у дошкольников Учитель – логопед Дудакова Людмила Геннадьевна
Содержание логопедической работы по формированию самоконтроля у дошкольников Учитель – логопед Дудакова Людмила Геннадьевна Клиническая анатомия мозгового отдела головы, применительно к операциям на мозговом черепе для студентов
Клиническая анатомия мозгового отдела головы, применительно к операциям на мозговом черепе для студентов Лицом к Лицу. Рекламная кампания
Лицом к Лицу. Рекламная кампания Государственный долг внешний и внутренний Бурсаковский Сергей Т093
Государственный долг внешний и внутренний Бурсаковский Сергей Т093  Совершенствование управления таможенных органов в условиях членства России в ВТО Подготовили: Орехова В. Очаева З. Подмарькова
Совершенствование управления таможенных органов в условиях членства России в ВТО Подготовили: Орехова В. Очаева З. Подмарькова  Электроника. Основные требования к электронным приборам
Электроника. Основные требования к электронным приборам Лабораторная диагностика аденовирусной и герпетической инфекции
Лабораторная диагностика аденовирусной и герпетической инфекции  Открытый конкурс в электронной форме МИР 2019
Открытый конкурс в электронной форме МИР 2019 Prezent
Prezent Хостел и коворкинг. Инвестиционное предложение
Хостел и коворкинг. Инвестиционное предложение Презентация "Санкт-Петербург-город мастеров кисти и резца" - скачать презентации по МХК
Презентация "Санкт-Петербург-город мастеров кисти и резца" - скачать презентации по МХК Пожарная безопасность в России
Пожарная безопасность в России Анализ использования основных фондов
Анализ использования основных фондов  Восстановление и сооружение земляного полотна в особых условиях
Восстановление и сооружение земляного полотна в особых условиях Язык UML
Язык UML Презентация на тему "Формирование речевого этикета у младших школьников на занятиях ГПД" - скачать презентации по Педагогике
Презентация на тему "Формирование речевого этикета у младших школьников на занятиях ГПД" - скачать презентации по Педагогике