Содержание
- 2. Сортировка 2 Дан массив a: array [1..n] of Ordinal Отрезок (сегмент) массива a[p..q] упорядочен: Sort (a,
- 3. Сортировка 3 Простые алгоритмы сортировки Сортировка выбором Идея. Пример. Список (удаление и вставка) Устойчивость сортировки –
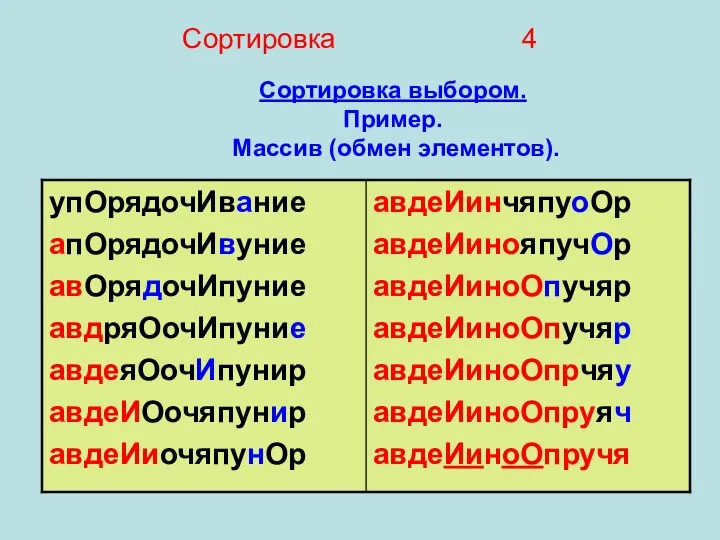
- 4. Сортировка 4 Сортировка выбором. Пример. Массив (обмен элементов).
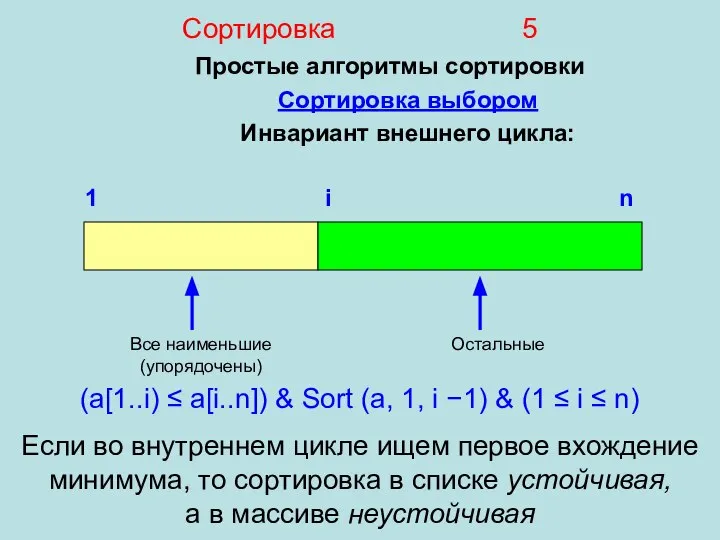
- 5. Сортировка 5 Простые алгоритмы сортировки Сортировка выбором Инвариант внешнего цикла: Все наименьшие (упорядочены) Остальные 1 i
- 6. Сортировка 6 Сортировка выбором for i:=1 to n−1 do begin {поиск минимума из a[i..n]} k :=
- 7. Сортировка 7 Анализ сортировки выбором Сi – число сравнений при выборе минимального элемента на i-ом шаге
- 8. Сортировка 8 Анализ сортировки выбором Пусть Mi – число перестановок на i-ом шаге, включая обновления текущего
- 9. Сортировка 9 Анализ сортировки выбором В среднем: Вероятность того, что произойдет обновление текущего минимума на j-ом
- 10. Анализ сортировки выбором в среднем В среднем за весь внешний цикл суммарное число перестановок есть Сортировка
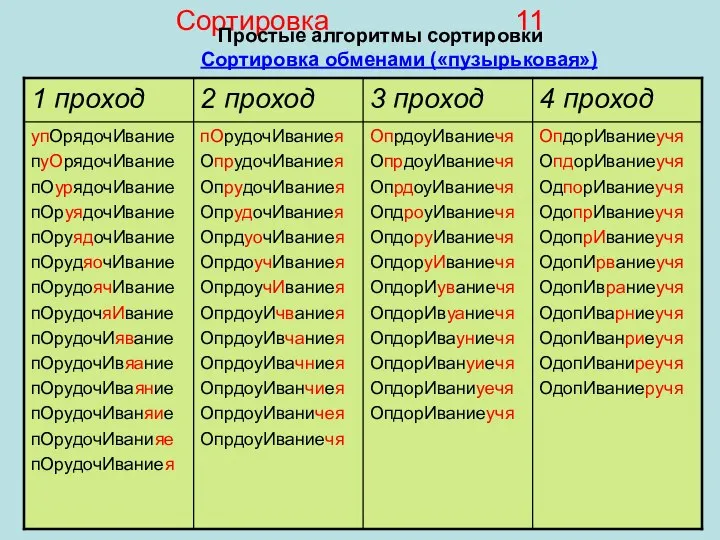
- 11. Сортировка 11 Простые алгоритмы сортировки Сортировка обменами («пузырьковая»)
- 12. Сортировка 12 Простые алгоритмы сортировки Сортировка обменами («пузырьковая») Продолжение
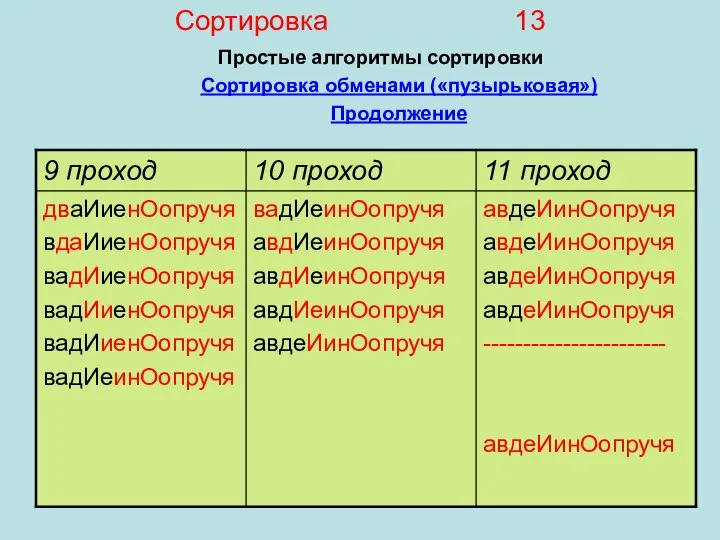
- 13. Сортировка 13 Простые алгоритмы сортировки Сортировка обменами («пузырьковая») Продолжение
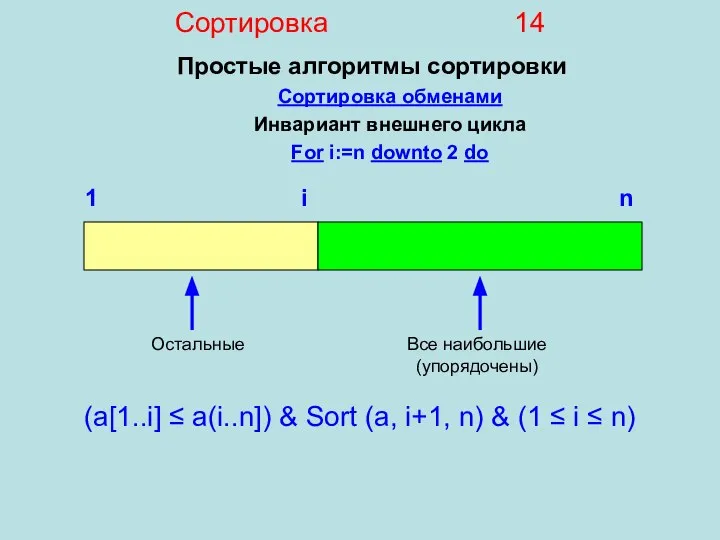
- 14. Сортировка 14 Простые алгоритмы сортировки Сортировка обменами Инвариант внешнего цикла For i:=n downto 2 do 1
- 15. Сортировка обменами (пузырьковая) for i:=n downto 2 do begin {просмотр a[1..i] с обменами соседних элементов} for
- 16. Анализ сортировки обменами (пузырьковой) Сортировка 16
- 17. Сортировка 17 Простые алгоритмы сортировки Сортировка вставками (включением)
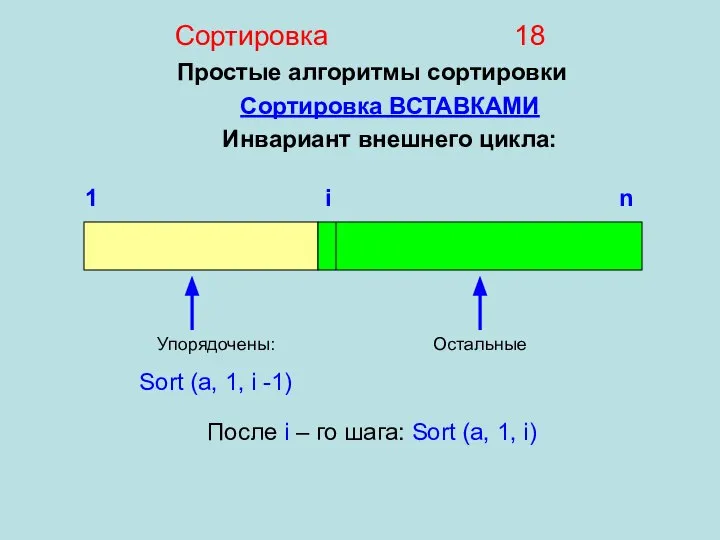
- 18. Сортировка 18 Простые алгоритмы сортировки Сортировка ВСТАВКАМИ Инвариант внешнего цикла: 1 i n Упорядочены: Sort (a,
- 19. Сортировка прямыми ВСТАВКАМИ Сортировка 19 j −1 0 1 x j i x x Sort (a,
- 20. Сортировка 20 Простые алгоритмы сортировки Сортировка ВСТАВКАМИ АЛГОРИТМ Прямые вставки (StraightInsertion) type index=0..nMax; index1=1..nMax; index2=0..nMax+1; mass=array
- 21. Сортировка 21 procedure StraightInsertion ( var a: mass; n: index1; k: index1 ); { сортировка массива
- 22. Сортировка 22 Сортировка ПРЯМЫМИ ВСТАВКАМИ Анализ Число сравнений ≈ число перемещений. Число сравнений на i –ом
- 23. Сортировка БИНАРНЫМИ ВСТАВКАМИ for i:=2 to n do begin { Найти место a[i] среди a[1..i-1] }
- 24. Сортировка БИНАРНЫМИ ВСТАВКАМИ Анализ алгоритма Число сравнений на i –ом шаге Ci ≤ ⎡log2i⎤. По всем
- 25. Сортировка 25 Быстрая сортировка (QuickSort) Основа – процедура разделения Partition ≤ x > x Инвариант цикла:
- 26. Сортировка 26 Быстрая сортировка (QuickSort) procedure Partition1 ( var a : mass; m, n: index1; var
- 27. while q begin if a[q] else if a[p] > x then p := p-1 else {
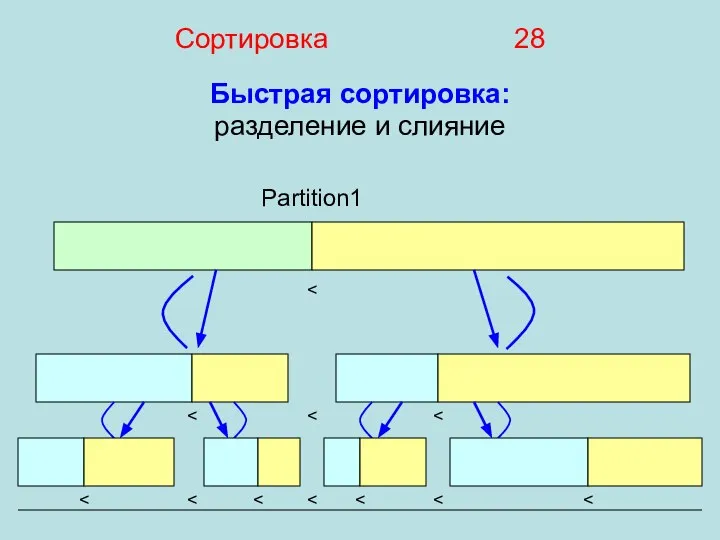
- 28. Быстрая сортировка: разделение и слияние Сортировка 28 Partition1
- 29. Сортировка 29 procedure Sortp1 (var a: mass; m, n: index1; k: index1 ); var p, q:
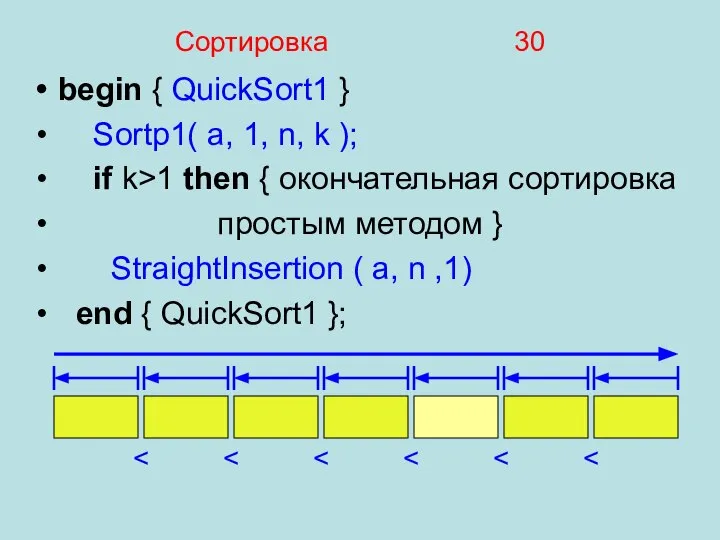
- 30. Сортировка 30 begin { QuickSort1 } Sortp1( a, 1, n, k ); if k>1 then {
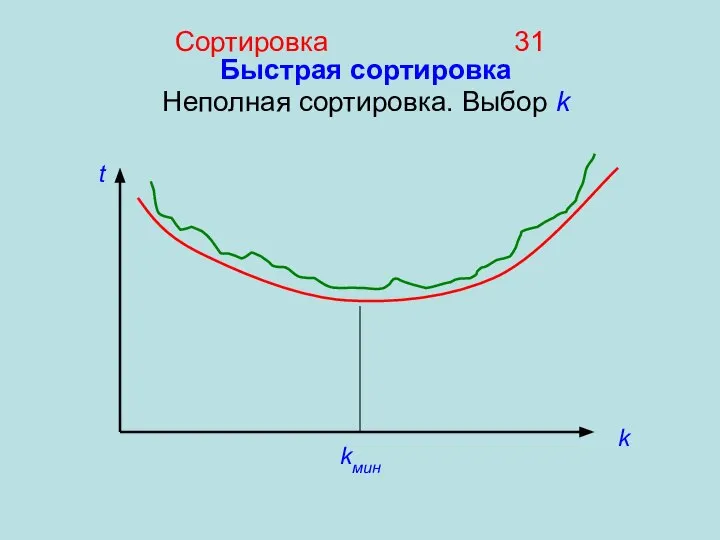
- 31. Быстрая сортировка Неполная сортировка. Выбор k Сортировка 31 k kмин t
- 32. Первый вызов Partition 32 1 2 3 4 5 6 7 8 9 10 11 12
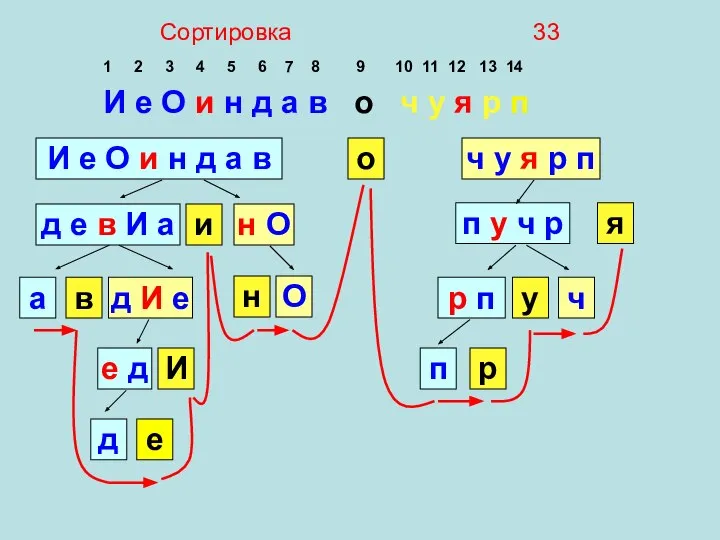
- 33. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 И е
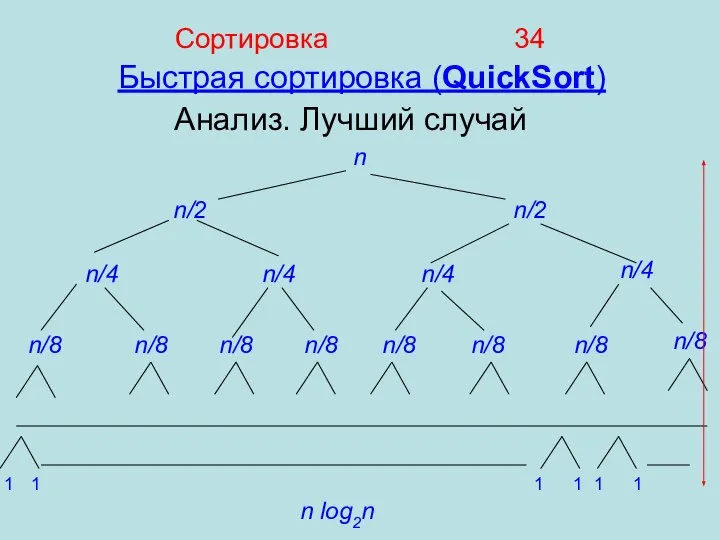
- 34. Сортировка 34 Анализ. Лучший случай Быстрая сортировка (QuickSort) n/2 n n/2 n/4 n/4 n/4 n/4 n/8
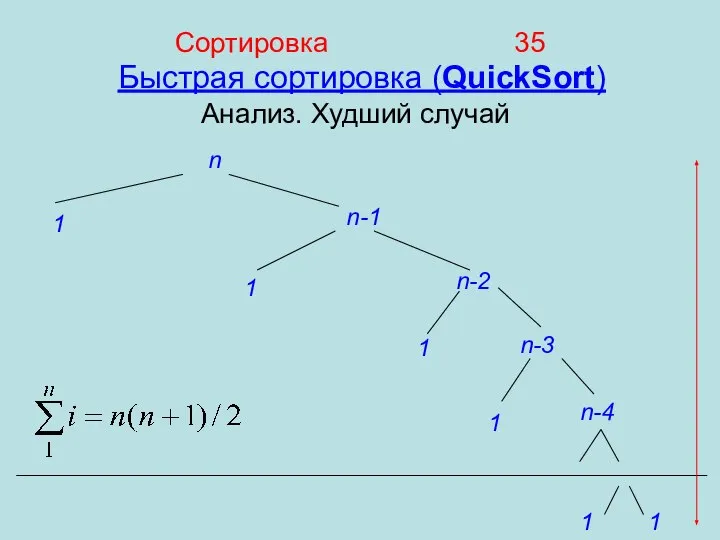
- 35. Сортировка 35 Анализ. Худший случай Быстрая сортировка (QuickSort) n n-1 n-2 1 1 1 n-3 n-4
- 36. Сортировка 36 Быстрая сортировка (QuickSort) Анализ. Промежуточный случай
- 37. Анализ. В среднем Сортировка 37 Быстрая сортировка (QuickSort) i 1 n
- 38. Анализ. В среднем (продолжение) Сортировка 38 Быстрая сортировка (QuickSort)
- 39. Анализ. В среднем (продолжение) Сортировка 39 Быстрая сортировка (QuickSort)
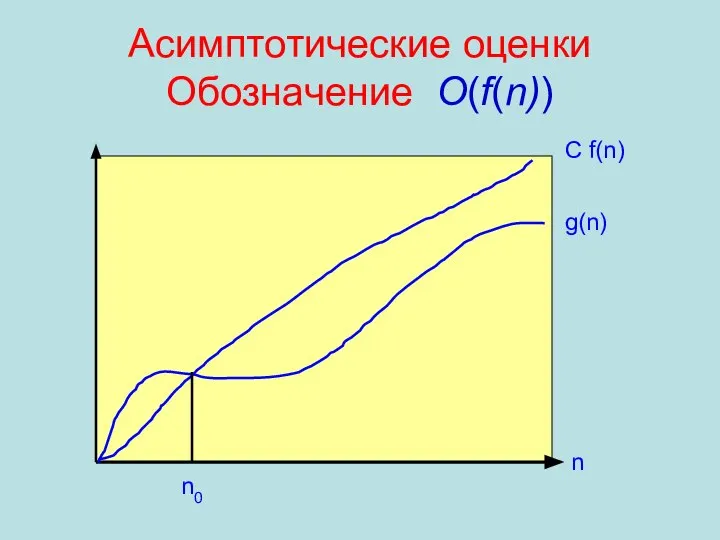
- 40. Для указания множества функций, которые не более чем в постоянное число раз превосходят f (n) при
- 41. Асимптотические оценки Обозначение О(f(n)) g(n) C f(n) n0 n
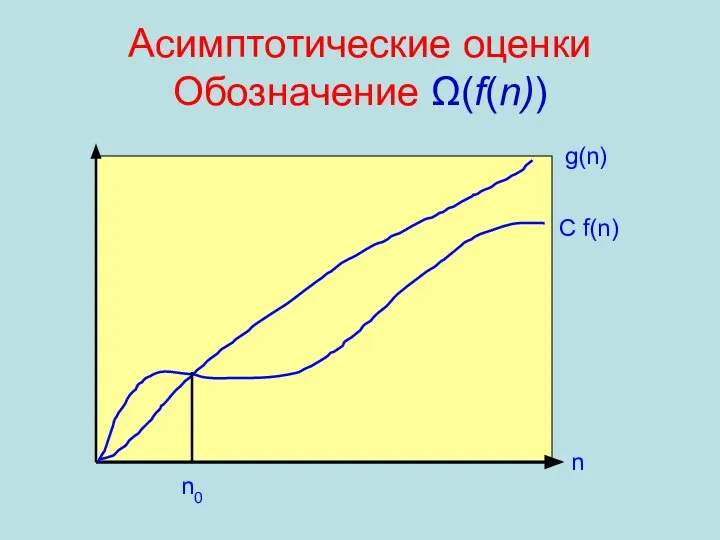
- 42. Асимптотические оценки Обозначения О(f(n)), Ω(f(n)), Θ(f(n)) Для указания множества функций, которые не менее чем в постоянное
- 43. Асимптотические оценки Обозначение Ω(f(n)) g(n) C f(n) n0 n
- 44. Асимптотические оценки Обозначения О(f(n)), Ω(f(n)), Θ(f(n)) Для указания множества функций того же порядка, что и f
- 46. Скачать презентацию
![Сортировка 2 Дан массив a: array [1..n] of Ordinal Отрезок (сегмент)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301818/slide-1.jpg)







![Сортировка обменами (пузырьковая) for i:=n downto 2 do begin {просмотр a[1..i]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301818/slide-14.jpg)










![while q begin if a[q] else if a[p] > x then](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301818/slide-26.jpg)









 Презентация "Рынок факторов производства: рынок земли" - скачать презентации по Экономике
Презентация "Рынок факторов производства: рынок земли" - скачать презентации по Экономике Внутреннее убранство православного храма
Внутреннее убранство православного храма Числовые характеристики одномерных и двумерных случайных величин
Числовые характеристики одномерных и двумерных случайных величин To Pouring Pattern Stripping & return Manipulator on jib crane Pattern Change
To Pouring Pattern Stripping & return Manipulator on jib crane Pattern Change Массовая и элитарная культура
Массовая и элитарная культура Технологические циклы
Технологические циклы глагол to be
глагол to be Материально-техническое обеспечение спортивных сооружений. Протезы
Материально-техническое обеспечение спортивных сооружений. Протезы Становление белорусской государственности
Становление белорусской государственности Шаблон презентации
Шаблон презентации Презентация по МХК Боги древнего Египта
Презентация по МХК Боги древнего Египта  Качество и сертификация
Качество и сертификация Асбестовский экономический колледж. Итоговая квалификационная работа. Направление(специальность):Оператор ПЭВМ (72)
Асбестовский экономический колледж. Итоговая квалификационная работа. Направление(специальность):Оператор ПЭВМ (72) Чередующиеся корни
Чередующиеся корни Виды кадровой политики
Виды кадровой политики Бенджамин Франклин
Бенджамин Франклин Тест
Тест  Бизнес-план компании «Монолит» - производство строительных материалов. Проект по экономике и экономической географии ученика
Бизнес-план компании «Монолит» - производство строительных материалов. Проект по экономике и экономической географии ученика  Мастер класс “С чего начать: Подготовка и создание архивов открытого доступа» Ирина Кучма, менеджер программы Открытый доступ, eIFL.net Презентация на совместном семинаре eIFL.net и ГПНТБ России «Открытый доступ и открытые архивы информации», 11 июня
Мастер класс “С чего начать: Подготовка и создание архивов открытого доступа» Ирина Кучма, менеджер программы Открытый доступ, eIFL.net Презентация на совместном семинаре eIFL.net и ГПНТБ России «Открытый доступ и открытые архивы информации», 11 июня Рак легкого
Рак легкого Презентация____
Презентация____ Синтоизм и его суть
Синтоизм и его суть Изменение имён прилагательных по родам - презентация для начальной школы__________________________________________________________________________________________________________
Изменение имён прилагательных по родам - презентация для начальной школы__________________________________________________________________________________________________________ Тема 1.3 Основы организации и нормирования труда ЧАСТЬ 2 нормирование труда
Тема 1.3 Основы организации и нормирования труда ЧАСТЬ 2 нормирование труда Разрезы и их виды в чертежах
Разрезы и их виды в чертежах Дополнительные взыскания и порядок их применения по трудовому законодательству РФ
Дополнительные взыскания и порядок их применения по трудовому законодательству РФ Ремонт и обслуживание тепловентилятора
Ремонт и обслуживание тепловентилятора Сінтаксіс і пунктуацыя. Сказы з параўнальнымі зваротамі
Сінтаксіс і пунктуацыя. Сказы з параўнальнымі зваротамі