Содержание
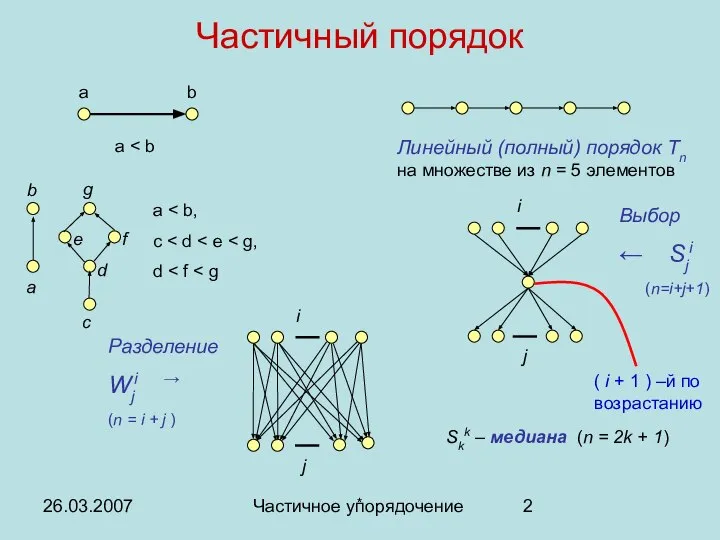
- 2. 26.03.2007 Частичное упорядочение Частичный порядок * Выбор ← Sji (n=i+j+1) ( i + 1 ) –й
- 3. 26.03.2007 Частичное упорядочение Выбор k-го элемента Синонимы: порядковые статистики, ранги, ранговые статистики Даны: список из n
- 4. 26.03.2007 Частичное упорядочение Выбор k-го элемента Алгоритм на основе процедуры Partition x – элемент массива, p-й
- 5. 26.03.2007 Частичное упорядочение Алгоритм на основе процедуры Partition Proc Select (a, L, R, k); var p:
- 6. 26.03.2007 Частичное упорядочение Алгоритм на основе процедуры Partition Анализ алгоритма Благоприятный случай – деление пополам 2.
- 7. 26.03.2007 Частичное упорядочение Линейный алгоритм выбора k-го элемента (В худшем случае) Идея: 1. Находить гарантированно «удачный»
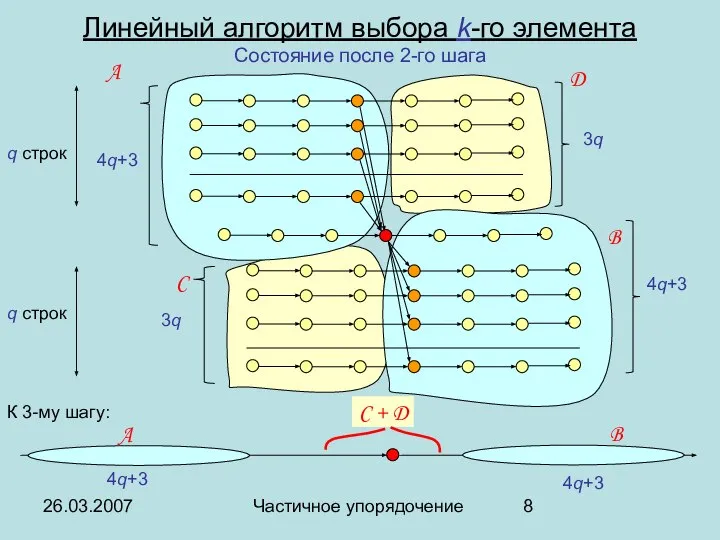
- 8. 26.03.2007 Частичное упорядочение Линейный алгоритм выбора k-го элемента Состояние после 2-го шага q строк q строк
- 9. 26.03.2007 Частичное упорядочение Линейный алгоритм выбора k-го элемента Шаг 3. «Разбрасываем» 6q элементов из C +
- 10. 26.03.2007 Частичное упорядочение Линейный алгоритм выбора k-го элемента Шаг 4. Рекурсивный вызов «вправо» или «влево» от
- 11. 26.03.2007 Частичное упорядочение Линейный алгоритм выбора k-го элемента Покажем, что T(n) = O(n) . Пусть T(n)
- 12. 26.03.2007 Частичное упорядочение Линейный алгоритм выбора k-го элемента Этот алгоритм лучше, чем прямая сортировка, при n
- 13. 26.03.2007 Частичное упорядочение Метод Prune & Search или Отсечение и Поиск
- 14. 26.03.2007 Частичное упорядочение Метод Prune & Search или Отсечение и Поиск
- 15. 26.03.2007 Частичное упорядочение Объява про текущий контроль по разделу «Сортировка»
- 17. Скачать презентацию












 Развитие самостоятельной и творческой активности учащихся на уроках математики в условиях введения ФГОС
Развитие самостоятельной и творческой активности учащихся на уроках математики в условиях введения ФГОС Презентация на тему "Правила поведения для воспитанных детей" - скачать презентации по Педагогике
Презентация на тему "Правила поведения для воспитанных детей" - скачать презентации по Педагогике Муниципальное образовательное учреждение Средняя общеобразовательная школы № 76
Муниципальное образовательное учреждение Средняя общеобразовательная школы № 76 Симптоматология заболеваний желчевыделительной системы
Симптоматология заболеваний желчевыделительной системы Вечные и земные ценности
Вечные и земные ценности Культура стран халифата
Культура стран халифата Глаголы с изменяющейся корневой гласной
Глаголы с изменяющейся корневой гласной Все подвиги Геракл совершил на службе А) у Зевса Б) у Эврисфея В) у Алкмены
Все подвиги Геракл совершил на службе А) у Зевса Б) у Эврисфея В) у Алкмены ЧЕМ БОЛЕЛ ВЕЛИКИЙ ВАН ГОГ? La tristesse durera toujours («Печаль будет длиться вечно»)
ЧЕМ БОЛЕЛ ВЕЛИКИЙ ВАН ГОГ? La tristesse durera toujours («Печаль будет длиться вечно»)  Радиационный контроль объектов и территорий
Радиационный контроль объектов и территорий Презентация Государственный флаг РФ
Презентация Государственный флаг РФ Опыт использования бизнес-моделей в процессе обучения предпринимательству в магистратуре Екатерина Бузулукова к.э.н., ст.преп
Опыт использования бизнес-моделей в процессе обучения предпринимательству в магистратуре Екатерина Бузулукова к.э.н., ст.преп Теоретические основы развития зависимого поведения у детей и подростков
Теоретические основы развития зависимого поведения у детей и подростков  Метрические свойства проекций. (Лекция 3)
Метрические свойства проекций. (Лекция 3) нейропсихология
нейропсихология Non scholae, sed vitae discimus
Non scholae, sed vitae discimus Tea tradition in Britain
Tea tradition in Britain Вещества и растворы для обеззараживания
Вещества и растворы для обеззараживания Семейная компания Bandi. Профессиональная косметика
Семейная компания Bandi. Профессиональная косметика Тема урока: Здоровый человек – здоровый сон. О правильном питании.
Тема урока: Здоровый человек – здоровый сон. О правильном питании. Федор Александрович Васильев Подготовила ученица 10 класса Бутикова Мария
Федор Александрович Васильев Подготовила ученица 10 класса Бутикова Мария Управленческие решения в организациях
Управленческие решения в организациях Древнегреческая вазопись, как яркий пример античного искусства
Древнегреческая вазопись, как яркий пример античного искусства ФИНАНСОВЫЙ КРИЗИС: причины возникновения и пути выхода Берзон Н.И. Д.э.н., профессор,
ФИНАНСОВЫЙ КРИЗИС: причины возникновения и пути выхода Берзон Н.И. Д.э.н., профессор, Карданные передачи
Карданные передачи Комбинационные узлы
Комбинационные узлы Китай
Китай Этика приветствий и представлений
Этика приветствий и представлений