Числовые характеристики одномерных и двумерных случайных величин

Характеристики двумерной случайной величины (ξ, η) – это характеристики одномерных величин

Ковариация

Определение. Ковариацией случайной величины (ξ, η) называется центральный смешанный момент второго

Ковариация

Величины ξ,η называются
некоррелированными при cov(ξ, η) = 0,
положительно

Коэффициент корреляции

Определение. Коэффициентом корреляции между случайными
величинами ξ, η называется число

Свойства коэффициента корреляции

1. │ρξη│≤ 1.
2. Если ξ,η независимы, то ρξη= 0.

Смысл коэффициента корреляции

Коэффициент корреляции есть мера линейной зависимости между ξ,

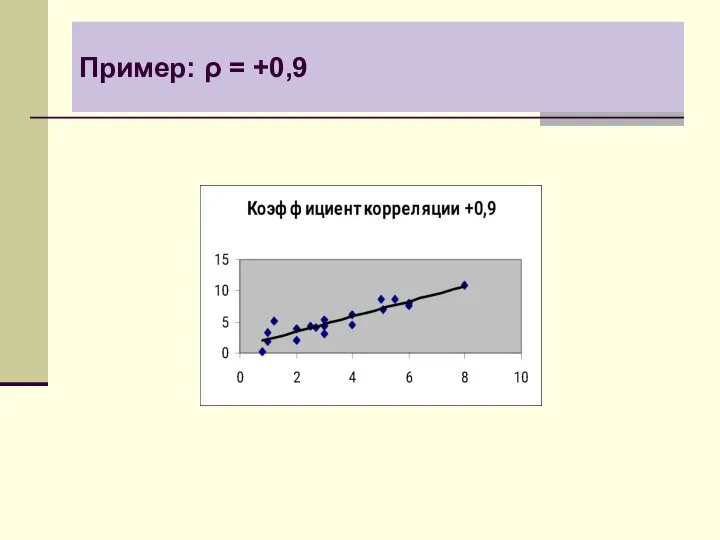
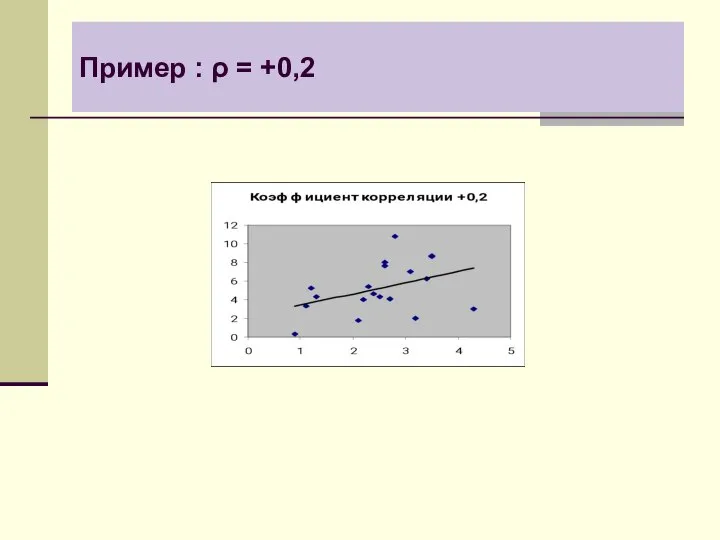
Пример: ρ = +0,9

Пример : ρ = +0,2

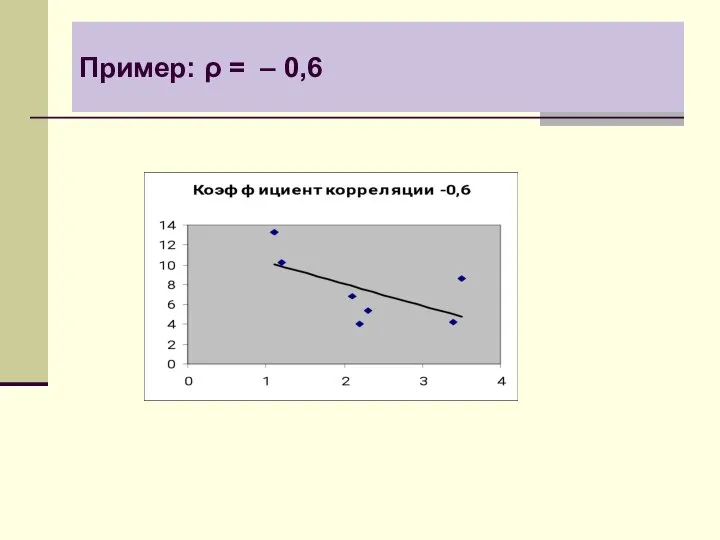
Пример: ρ = – 0,6

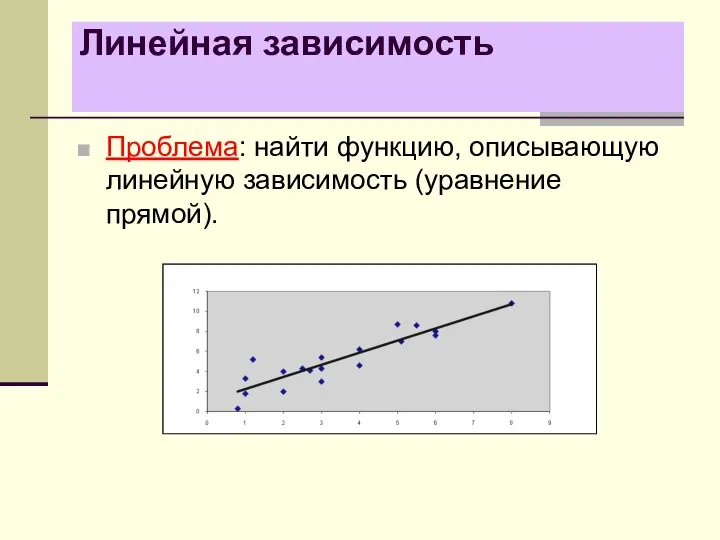
Линейная зависимость

Проблема: найти функцию, описывающую линейную зависимость (уравнение прямой).

Уравнение линейной регрессии

Определение. Уравнением линейной регрессии η на ξ называется уравнение

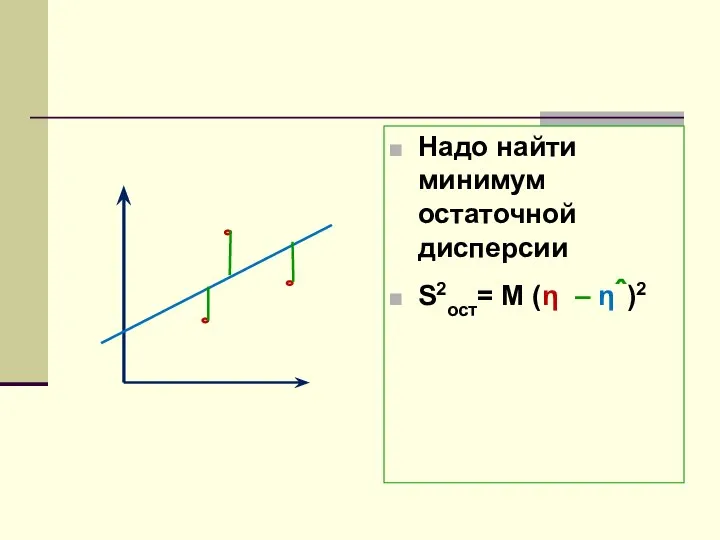
Надо найти минимум остаточной дисперсии
S2ост= M (η – ηˆ)2

Нахождение коэффициентов уравнения линейной регрессии

S2ост = M[η – (aξ+b)]2 =
M[(η

(Mη – aMξ – b) – постоянная величина, ее можно вынести

Поскольку M(η – Mη)2 = Dη = σ2η,
M(ξ – M

S2ост – функция переменных a и b, надо найти min

S2ост = σ2η+ a2σ2ξ + (Mη – aMξ – b)2 –

Подставим
a = ρ∙ση/σξ, b = Mη – aMξ
В уравнение ηˆ=

Замечание

Коэффициент уравнения линейной регрессии ρ∙ση/σξ можно записать в виде:
ρ∙ση/σξ = cov(ξ,η)/σ2ξ.
Тогда

Остаточная дисперсия

Найдем значение S2ост = M(η – ηˆ)2 = M(η –

σ2η + (ρ∙ση)2 – 2 ρ2∙ση2 = σ2η – ρ2∙ση2 =
=

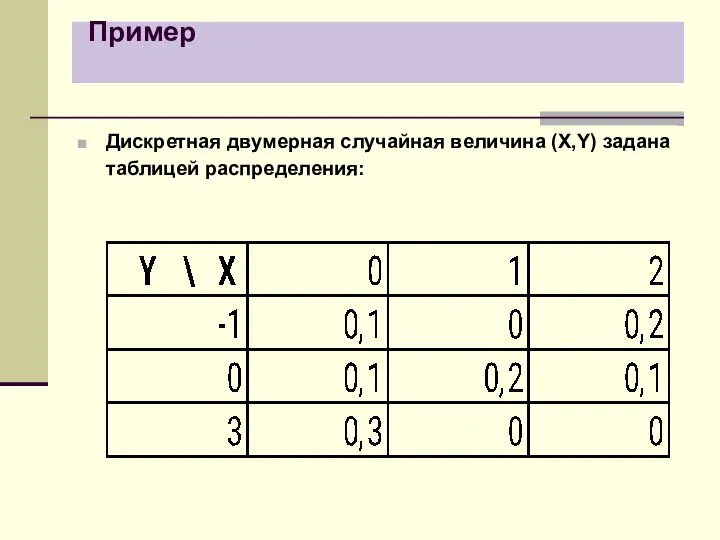
Пример

Дискретная двумерная случайная величина (X,Y) задана таблицей распределения:

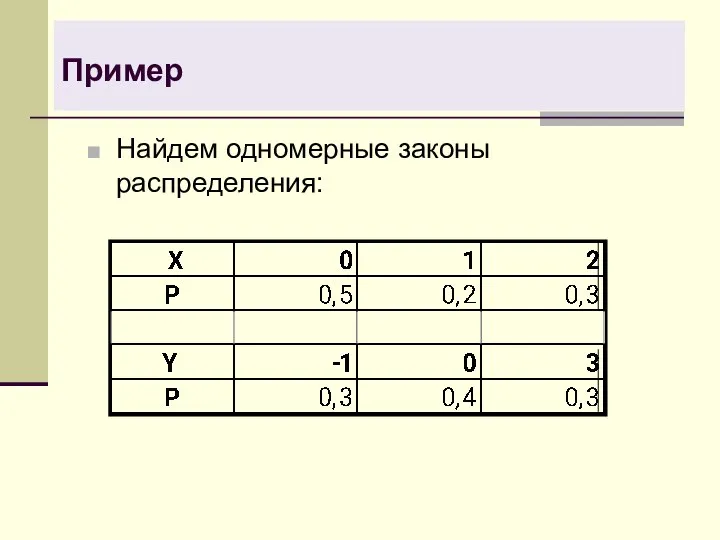
Пример

Найдем одномерные законы распределения:

Пример

Вычислим числовые характеристики.
MX = 0∙0,5 + 1∙0,2 + 2∙0,3 =

Пример

Найдем ковариацию:
cov(ξ, η) = M(ξ∙η) – M ξ∙ M η.
В

Коэффициент корреляции

Уравнение линейной регрессии
Запишем уравнение линейной регрессии Y на X.
Подставим MX =

Остаточная дисперсия

Yˆ – 0,6 = – 1,16(X – 0,8).
Yˆ= – 1,16X

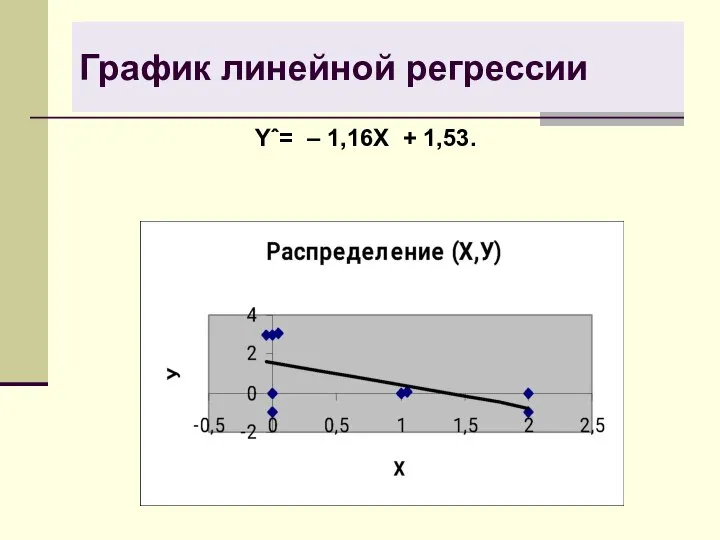
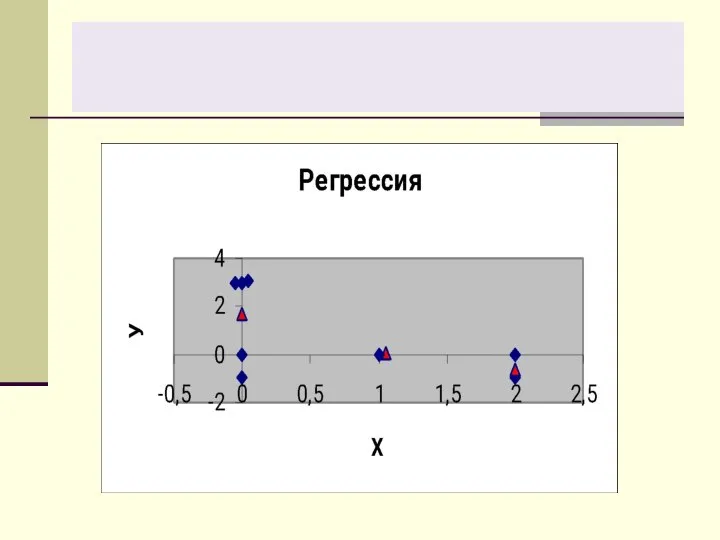
График линейной регрессии

Yˆ= – 1,16X + 1,53.

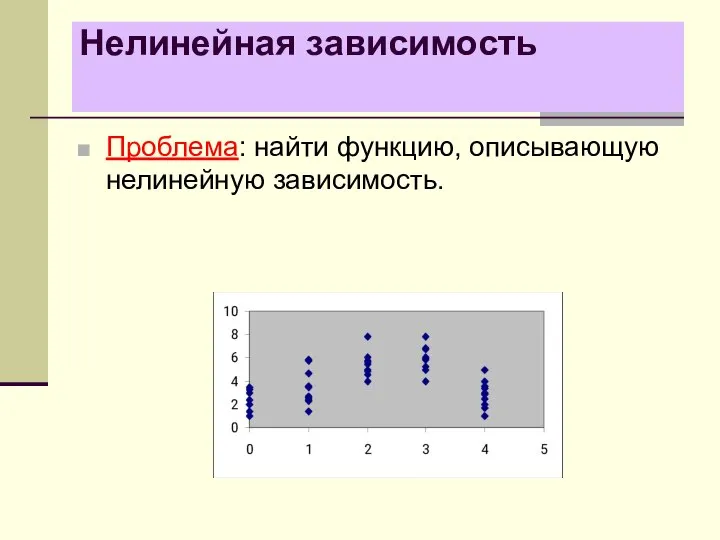
Нелинейная зависимость

Проблема: найти функцию, описывающую нелинейную зависимость.

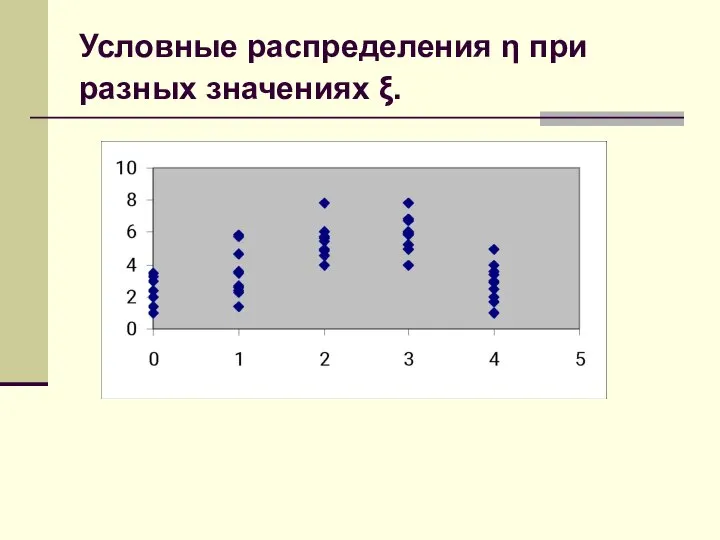
Условные распределения

Пусть (ξ, η) – двумерная случайная величина. Рассмотрим распределение η

Условные распределения η при разных значениях ξ.

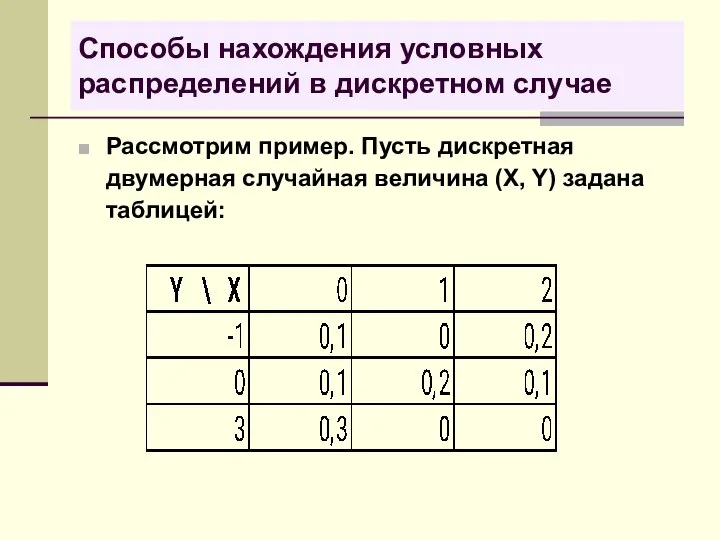
Способы нахождения условных распределений в дискретном случае

Рассмотрим пример. Пусть дискретная двумерная

Пример

Найдем условный закон распределения Y/X = 0:

Действительно,
P(Y = –1/X = 0) = P(Y = –1, X

Найдем другие условные законы.
Условный закон распределения Y/X = 1:

Такой закон распределения записывается в виде ряда распределения

Условный закон распределения Y/X=2:

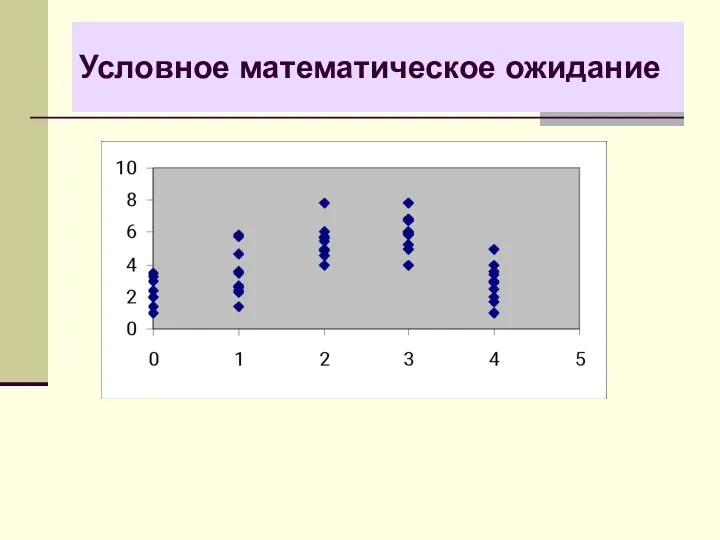
Условное математическое ожидание

Определение. Условным математическим ожиданием случайной
величины η при условии,

Замечание

Условное математическое ожидание обладает свойствами математического ожидания .

Условное математическое ожидание

Вспомним предыдущий пример.

Найдем условное матожидание Y/X=0:
M(Y/X=0)= (–1)∙1/5 + 0∙1/5 +

Аналогично, условные матожидания
M(Y/X=1) = 0∙1 =0,
M(Y/X=2) = (–1)∙2/3 + 0∙1/3

Регрессия

Определение. Регрессией η на ξ называется случайная величина r(ξ), равная при

Пример

В условиях предыдущего примера регрессия Y на X равна:

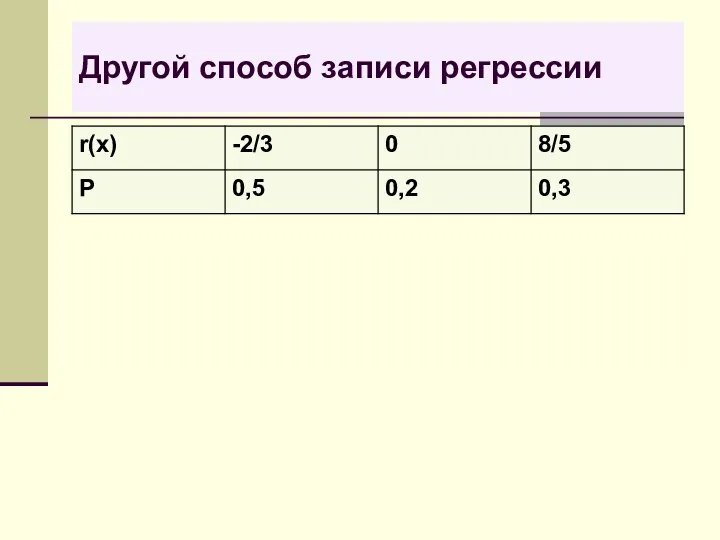
Другой способ записи регрессии

Корреляционное отношение

Определение. Корреляционным отношением η на ξ называется числовая характеристика, равная

Свойства корреляционного отношения

1. 0 ≤ θ2η,ξ ≤ 1.
2. θ2η,ξ ≥ ρ2.
3.

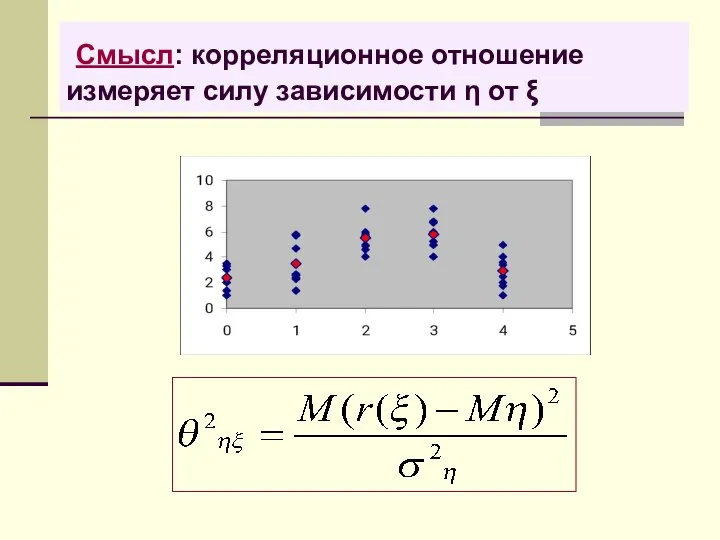
Смысл: корреляционное отношение измеряет силу зависимости η от ξ

Пример.

Чтобы найти θ2YX, надо сначала найти MY и DY.
Мы их недавно

MY = ( –1)∙0,3 + 0∙0,4 + 3∙0,3 = 0,6.
DY

Смысл полученного числа: корреляционное отношение измеряет силу зависимости Y от X.

Чем

Условные распределения

Определение. Условной функцией распределения случайной величины
η при условии, что

Условная плотность

Определение. Если условная функция распределения случайной величины η при условии,

Нахождение условной функции распределения

Условная функция распределения случайной величины η при

Нахождение условной плотности распределения

Условная плотность распределения сл. в. η при условии,

Поскольку

Числовые характеристики многомерных случайных величин

Определение. Ковариационной матрицей случайных величин ξ1, ξ2

Ковариационная матрица К

Корреляционная матрица R

Наряду с ковариационной матрицей рассматривают и матрицу R, составленную

Уравнение множественной линейной регрессии

Рассмотрим случайные величины
ξ0 ξ1, ξ2 ,

Определение. Уравнением линейной регрессии ξ0 на ξ1, ξ2 , …, ξn

Здесь bi (i =1,…, n) – параметры, минимизирующие остаточную дисперсию

Минимизируя остаточную дисперсию, получаем, что

Остаточная дисперсия

Здесь и далее через Rij обозначено алгебраическое дополнение элемента

Частный коэффициент корреляции

Частный коэффициент корреляции используется как мера линейной зависимости между