Содержание
- 2. 09/02/2023 Суть метода сеток Суть метода сеток в том, что решение ДУ получают в виде достаточно
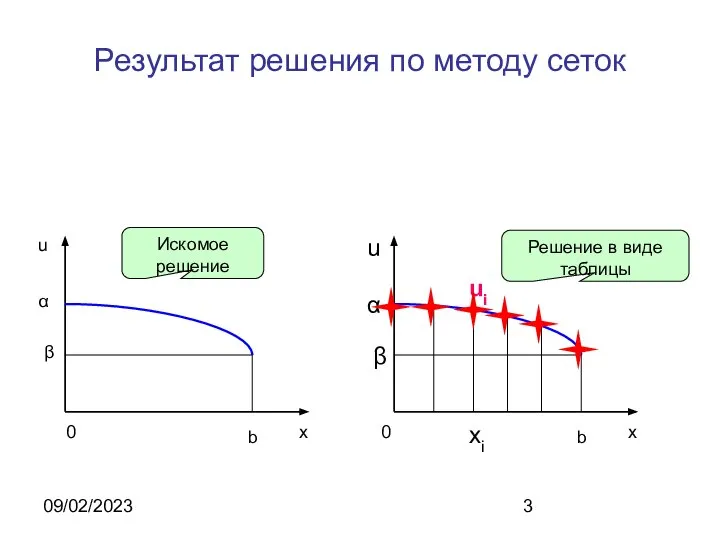
- 3. 09/02/2023 Результат решения по методу сеток x b 0 α u β x b 0 α
- 4. 09/02/2023 Построение сетки Сетка представляет собой набор узлов (точек), «равномерно» распределенных по области Ω. Множество таких
- 5. 09/02/2023 Получение конечноразностной схемы Решение u(x) ищется в виде таблицы значений в узлах выбранной сетки дифференциальное
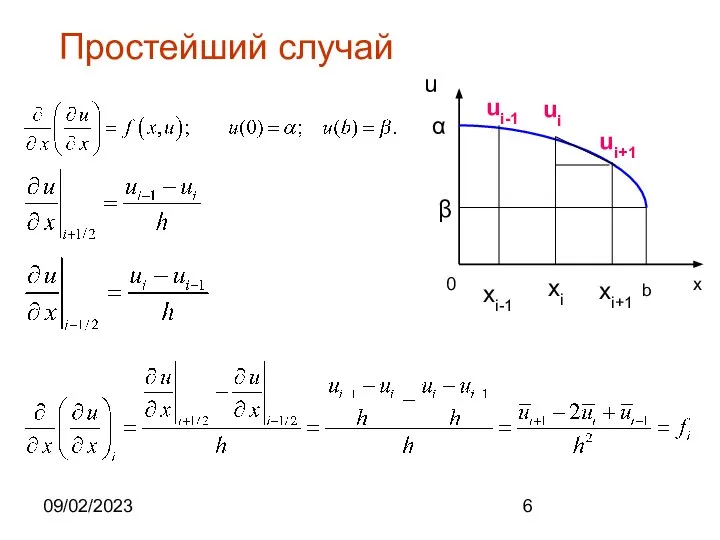
- 6. 09/02/2023 Простейший случай x b 0 α u β xi ui ui+1 ui-1 xi+1 xi-1
- 7. 09/02/2023 Интегроинтерполяционный способ получения конечно-разностной схемы область Ω =[0,b] разобьем на элементарные непересекающиеся подобласти, в центре
- 8. 09/02/2023 Интегроинтерполяционный способ (продолжение) Преобразуем Окончательно получим переобозначим
- 9. 09/02/2023 Решение системы конечно-разностных уравнений Стандартная система с трехдиагональной матрицей:
- 10. 09/02/2023 идея метода прогонки Прямым ходом метода Гаусса приводим систему к виду Ввиду того что матрица
- 11. 09/02/2023 Метод прогонки 1) прямой ход для 2) обратный ход для i от N до 1
- 12. 09/02/2023 Реализация метода прогонки c(1)=…; b(1)=…; d(1)=…; for i=2:N a(i)= b(i)= c(i)= d(i)= … end ks(1)=-c(1)/b(1);
- 13. 09/02/2023 Погрешность аппроксимации При замене дифференциального уравнения системой алгебраических уравнений вносится так называемая погрешность аппроксимации конечно-разностной
- 14. 09/02/2023 Нахождение и оценка погрешности аппроксимации После подстановки получаем: Используем начальные члены разложения в ряд Тейлора:
- 15. 09/02/2023 Оценка погрешности аппроксимации =0 В результате имеем:
- 16. 09/02/2023 Оценка погрешности решения Понятие устойчивости Погрешность решения : Для сходимости к точному решению кроме необходима
- 18. Скачать презентацию



![09/02/2023 Интегроинтерполяционный способ получения конечно-разностной схемы область Ω =[0,b] разобьем на](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1295301/slide-6.jpg)









 Экосистемы
Экосистемы Управление деловой карьерой в организации
Управление деловой карьерой в организации Политология, как наука о политике и ее взаимоотношениях с обществом
Политология, как наука о политике и ее взаимоотношениях с обществом Как жить в мире с родителями? Классный час
Как жить в мире с родителями? Классный час Исаак Ильич Левитан (1860-1900) Работу выполнил Тихачев Вячеслав ученик 5 «Б» класса МОУ лицея №10 Г. Советска
Исаак Ильич Левитан (1860-1900) Работу выполнил Тихачев Вячеслав ученик 5 «Б» класса МОУ лицея №10 Г. Советска Учебный план 1 класса на 2010-2011учебный год ГОУ СОШ с УИОП г.Белой Холуницы Кировской области
Учебный план 1 класса на 2010-2011учебный год ГОУ СОШ с УИОП г.Белой Холуницы Кировской области Аттестационная работа. Методическая разработка по выполнению исследовательской работы «Секреты колыбельной песни»
Аттестационная работа. Методическая разработка по выполнению исследовательской работы «Секреты колыбельной песни» Туризм. Грузия
Туризм. Грузия Личность Психопатии Олигофрения
Личность Психопатии Олигофрения Pancakes week, Maslenitsa
Pancakes week, Maslenitsa Облачные технологии как информационные сервисы Интернет
Облачные технологии как информационные сервисы Интернет Объектно-ориентированное программирование. Языки C++ и C#
Объектно-ориентированное программирование. Языки C++ и C# Кенигсберг – это крепость? Шумилина В.А.
Кенигсберг – это крепость? Шумилина В.А. Методы изучения наследственности человека
Методы изучения наследственности человека  Дипломатия и демократия. Дипломатия и переговоры
Дипломатия и демократия. Дипломатия и переговоры Фокина Л. П. Тренажёр-раскраска СЛОВАРНЫЕ СЛОВА. Часть 2 - презентация для начальной школы
Фокина Л. П. Тренажёр-раскраска СЛОВАРНЫЕ СЛОВА. Часть 2 - презентация для начальной школы Александр Карелин
Александр Карелин Презентация "Деревянне зодчество Руси" - скачать презентации по МХК
Презентация "Деревянне зодчество Руси" - скачать презентации по МХК Український національний костюм
Український національний костюм Классификация деловых культур по Р. Гестеланду
Классификация деловых культур по Р. Гестеланду Развитие натуралистических умений учащихся средствами изобразительного искусства
Развитие натуралистических умений учащихся средствами изобразительного искусства Презентация "Костюм xviii века" - скачать презентации по МХК
Презентация "Костюм xviii века" - скачать презентации по МХК “ҚАЗФОСФАТ” ЖШС
“ҚАЗФОСФАТ” ЖШС Современные перспективные технологии
Современные перспективные технологии Рекурсивные функции языка CLIPS
Рекурсивные функции языка CLIPS IT – Скорая. Организация по ремонту компьютеров
IT – Скорая. Организация по ремонту компьютеров Тренинг "Сплочение коллектива". Познание стран мира
Тренинг "Сплочение коллектива". Познание стран мира ЦИКЛИЧЕСКИЕ НУКЛЕОТИДЫ В РОЛИ ВТОРИЧНЫХ ПОСРЕДНИКОВ
ЦИКЛИЧЕСКИЕ НУКЛЕОТИДЫ В РОЛИ ВТОРИЧНЫХ ПОСРЕДНИКОВ