Содержание
- 2. СОДЕРЖАНИЕ Часть 1. Достижимость вершин. Часть 2. Базы дуг. Часть 3. Растущие ориентированные деревья.
- 3. Часть 1 Условия достижимости
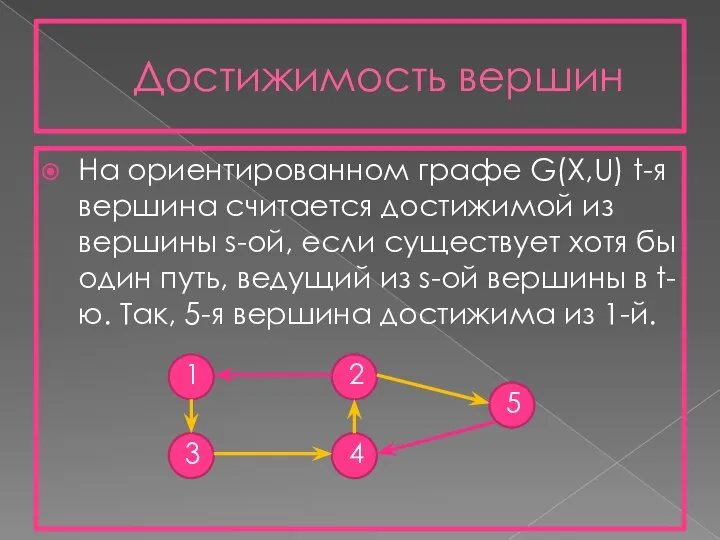
- 4. Достижимость вершин На ориентированном графе G(X,U) t-я вершина считается достижимой из вершины s-ой, если существует хотя
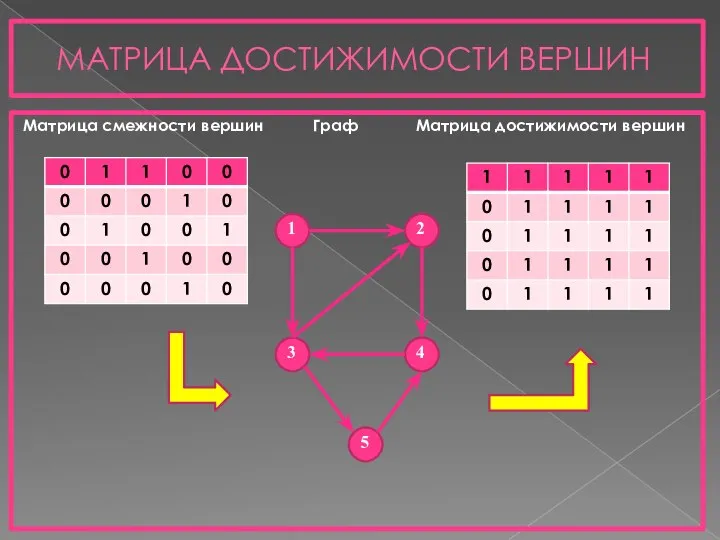
- 5. МАТРИЦА ДОСТИЖИМОСТИ ВЕРШИН Матрица смежности вершин Граф Матрица достижимости вершин 1 3 2 4 5
- 6. Часть 2 Базы дуг
- 7. БАЗА ДУГ - ОПРЕДЕЛЕНИЕ Базой дуг ориентированного графа G(X,U) с матрицей достижимости вершин «М» называется такое
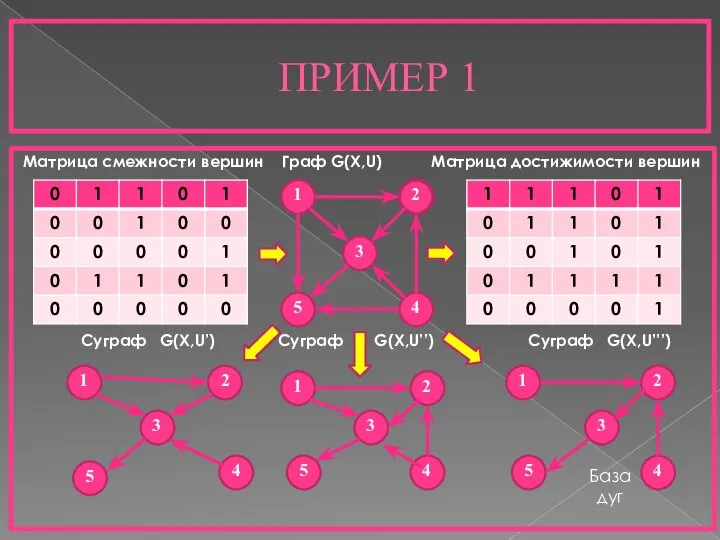
- 8. ПРИМЕР 1 Матрица смежности вершин Граф G(X,U) Матрица достижимости вершин Суграф G(X,U’) Суграф G(X,U’’) Суграф G(X,U’’’)
- 9. МИНИМАЛЬНАЯ БАЗА ДУГ - ОПРЕДЕЛЕНИЕ Минимальной базой дуг взвешенного ориентированного графа G(X,U) с матрицей достижимости вершин
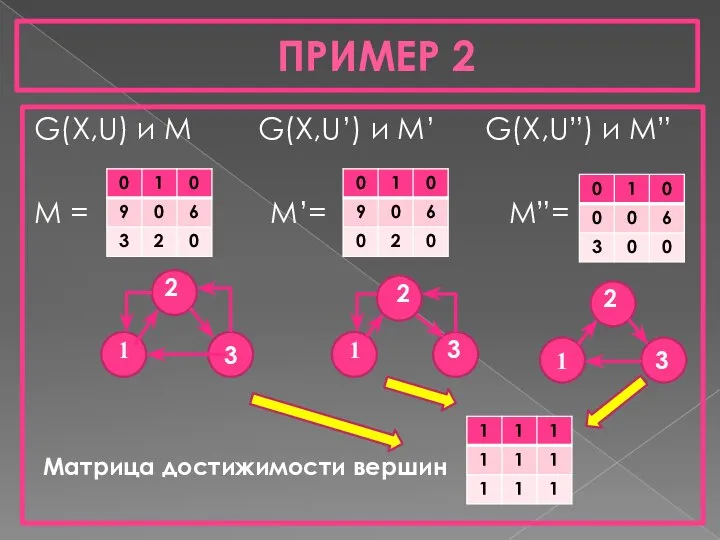
- 10. ПРИМЕР 2 G(X,U) и М G(X,U’) и M’ G(X,U”) и M” M = M’= M”= Матрица
- 11. СВОЙСТВА БАЗ ДУГ Теорема 1. Каждый ориентированный граф обладает по крайней мере одной базой дуг. Теорема
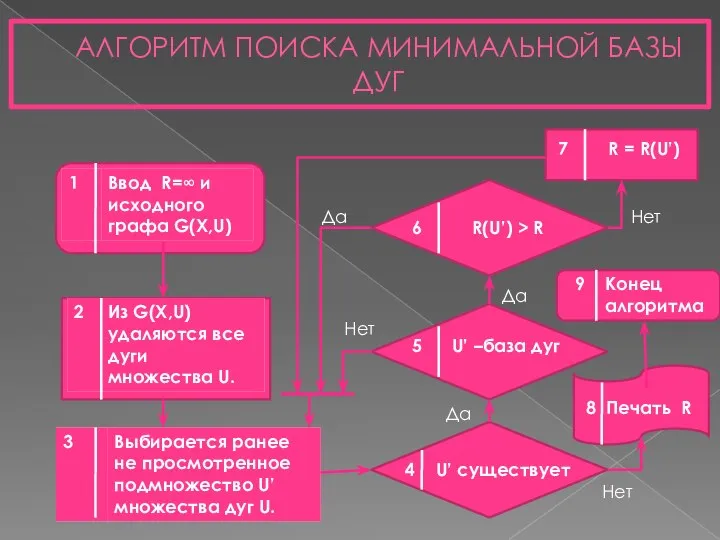
- 12. АЛГОРИТМ ПОИСКА МИНИМАЛЬНОЙ БАЗЫ ДУГ 4 U’ существует 5 U’ –база дуг 6 R(U’) > R
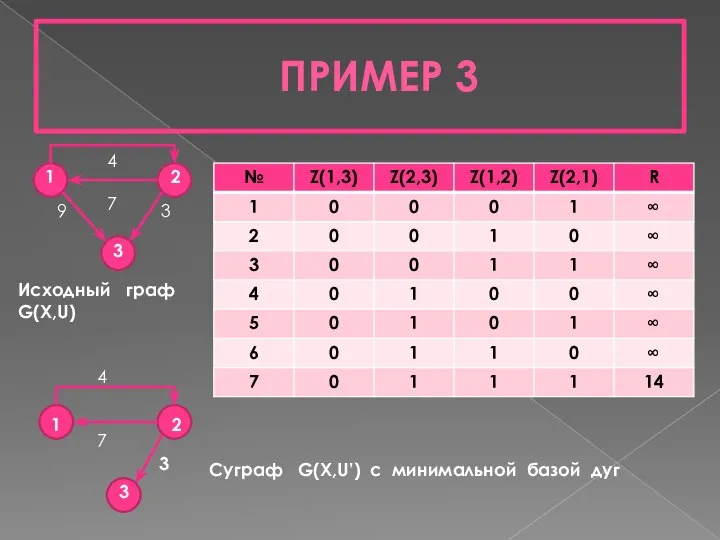
- 13. ПРИМЕР 3 1 2 1 2 3 3 4 7 4 7 9 3 3 Исходный
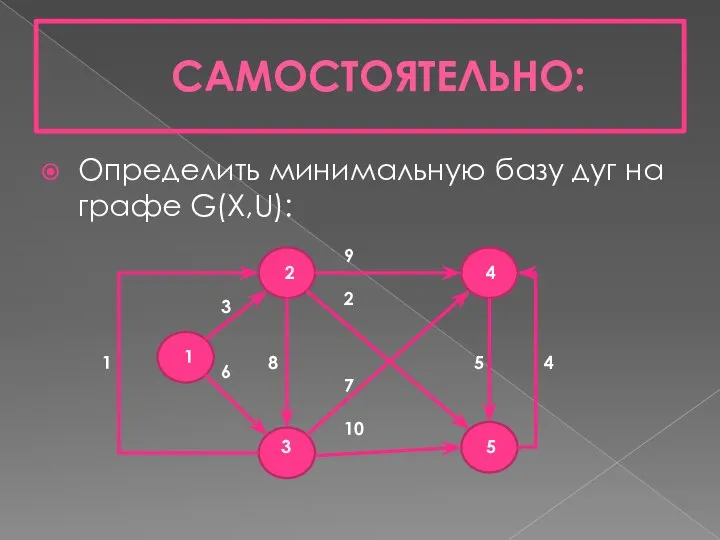
- 14. САМОСТОЯТЕЛЬНО: Определить минимальную базу дуг на графе G(X,U): 2 4 3 5 1 1 8 5
- 15. Часть 3 Растущие ориентированные деревья
- 16. МИНИМАЛЬНЫЕ РАСТУЩИЕ ОРИЕНТИРОВАННЫЕ ДЕРЕВЬЯ Содержательная постановка задачи: требуется на заданном взвешенном ориентированном графе G(X,U) выделить подграф
- 17. ОБОЗНАЧЕНИЯ И ОПРЕДЕЛЕНИЯ
- 18. ФОРМАЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ
- 19. СВОЙСТВА МИНИМАЛЬНЫХ РАСТУЩИХ ДЕРЕВЬЕВ Величина является нижней границей суммарного веса дуг минимального дерева. Если граф G(X,U)
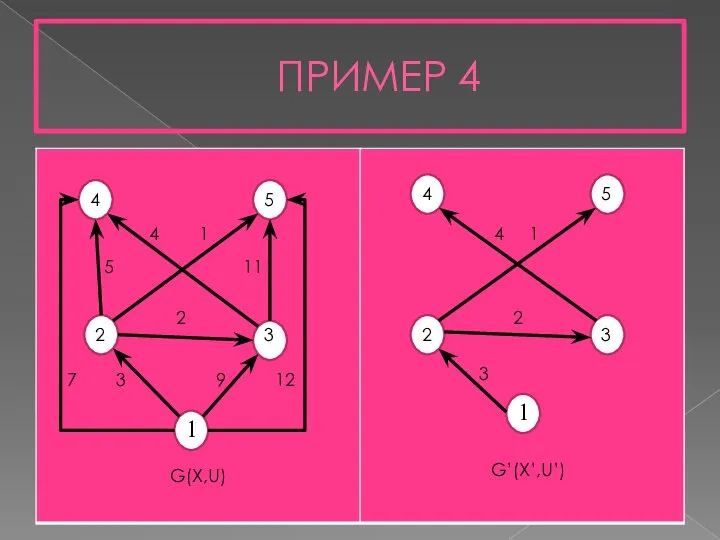
- 20. ПРИМЕР 4 1 1 2 3 2 3 4 5 4 5 7 3 9 12
- 21. АЛГОРИТМ ВЫДЕЛЕНИЯ МИНИМАЛЬНОГО ДЕРЕВА НА ГРАФЕ БЕЗ КОНТУРОВ Шаг 1. На исходном графе G(X,U) удаляются все
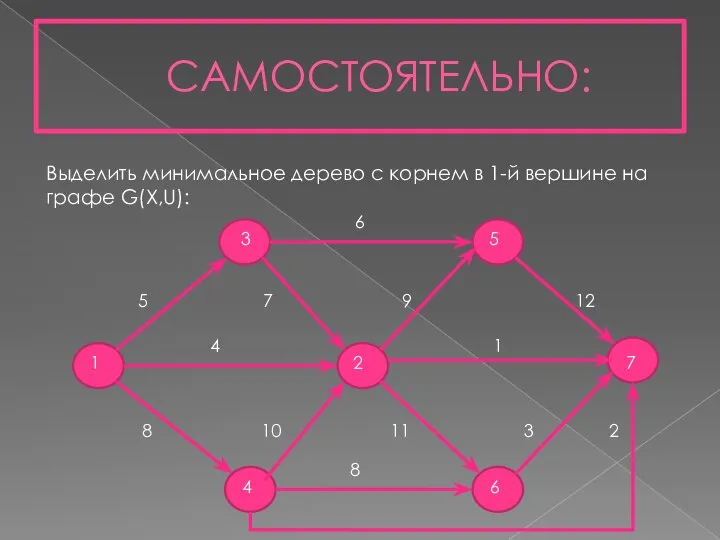
- 22. САМОСТОЯТЕЛЬНО: Выделить минимальное дерево с корнем в 1-й вершине на графе G(X,U): 1 2 7 3
- 23. ПЕРСОНАЛЬНЫЕ ЗАДАНИЯ На полученном орграфе: 1. Определить минимальный разрез. 2. Удалить дуги минимального разреза на исходном
- 24. ПЕРСОНАЛЬНЫЕ ЗАДАНИЯ 1 - 9
- 25. ПЕРСОНАЛЬНЫЕ ЗАДАНИЯ 10 - 18
- 26. ПЕРСОНАЛЬНЫЕ ЗАДАНИЯ 19 - 27
- 27. Алгоритм поиска минимального дерева на орграфе с бикомпонентами: шаги 1 - 3 Шаг 1. На исходном
- 28. Алгоритм поиска минимального дерева на орграфе с бикомпонентами: шаги 4 - 6 Шаг 4. Вершина j-я
- 29. Алгоритм поиска минимального дерева на орграфе с бикомпонентами: шаги 7 - 9 Шаг 7. На множестве
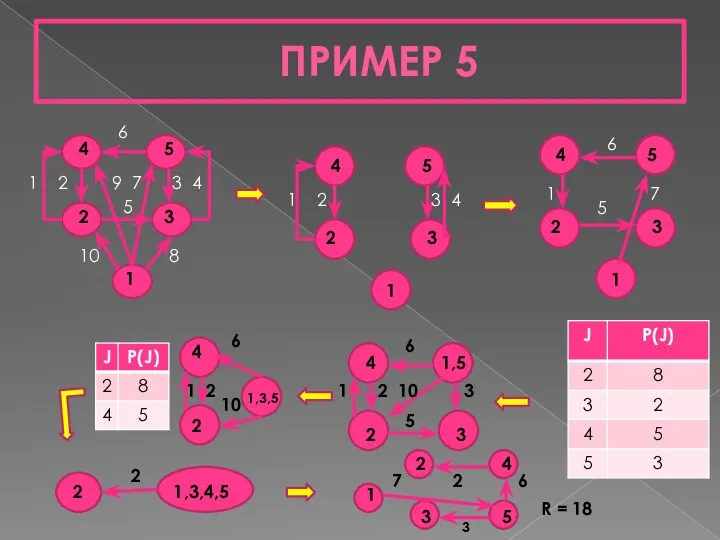
- 30. ПРИМЕР 5 1 2 9 7 3 4 10 8 4 5 2 3 1 4
- 32. Скачать презентацию



















 Федеральный закон «Об основах охраны здоровья граждан в РФ»
Федеральный закон «Об основах охраны здоровья граждан в РФ» Ремесло культуры Луншань
Ремесло культуры Луншань Праздник всех влюблённых
Праздник всех влюблённых The Hundred Years war Столетняя война
The Hundred Years war Столетняя война  «Букет роз» (материал-пластилин) Урок художественного труда 3 класс
«Букет роз» (материал-пластилин) Урок художественного труда 3 класс Бізнес-план кафе "White&black"
Бізнес-план кафе "White&black" Schüleraustausch, internationale Jugendprojekte
Schüleraustausch, internationale Jugendprojekte Общие сведения о языке программирования Паскаль
Общие сведения о языке программирования Паскаль The Geographical Position of Ukraine
The Geographical Position of Ukraine Сертификация сыра
Сертификация сыра Китайская Народная Республика –страна контрастов
Китайская Народная Республика –страна контрастов применение вывозных таможенных пошлин на нефть и нефтепродукты Мещерякова Юлия Т095
применение вывозных таможенных пошлин на нефть и нефтепродукты Мещерякова Юлия Т095  Формирование функции голосообразования у младших школьников в условиях школы второго вида Важенина Анна Александровна, учитель-
Формирование функции голосообразования у младших школьников в условиях школы второго вида Важенина Анна Александровна, учитель- Анализ данных
Анализ данных  Презентация "Система учета энергоресурсов, как основной инструмент энергетического менеджмента" - скачать презентации по Эк
Презентация "Система учета энергоресурсов, как основной инструмент энергетического менеджмента" - скачать презентации по Эк Аттестация сотрудников компании, осень 2018: итоги. Аттестация, весна 2019: планы
Аттестация сотрудников компании, осень 2018: итоги. Аттестация, весна 2019: планы Шасси и каркасы
Шасси и каркасы Анализ логистических рисков в цепи поставок
Анализ логистических рисков в цепи поставок  Шалаши, плоды и небо
Шалаши, плоды и небо Получение вакуума
Получение вакуума Система отдыха в Турции
Система отдыха в Турции Эстетика постимпрессионизма Урок МХК в 11 кл. Учитель: Е.А. Федюшина
Эстетика постимпрессионизма Урок МХК в 11 кл. Учитель: Е.А. Федюшина Микроволновой метод измерения удельного сопротивления полупроводниковых материалов
Микроволновой метод измерения удельного сопротивления полупроводниковых материалов Тайнопись работодателя Как «расшифровать» вакансию до собеседования? Ананьева Елизавета, редактор Rabota.ru Москва, 2011
Тайнопись работодателя Как «расшифровать» вакансию до собеседования? Ананьева Елизавета, редактор Rabota.ru Москва, 2011  Презентация Особенности регулирования труда лиц, работающих в районах Крайнего Севера и приравненных к ним местностях
Презентация Особенности регулирования труда лиц, работающих в районах Крайнего Севера и приравненных к ним местностях  Праздник Масленица
Праздник Масленица Лекарственные средства, влияющие на афферентную иннервацию
Лекарственные средства, влияющие на афферентную иннервацию  Строительство здания с ограждающей конструкцией из энергоэффективных мелкоштучных блоков
Строительство здания с ограждающей конструкцией из энергоэффективных мелкоштучных блоков