Содержание
- 2. САУ устойчива если после кратковременного возмущения она возвращается в прежнее или занимает новое устойчивое положение.
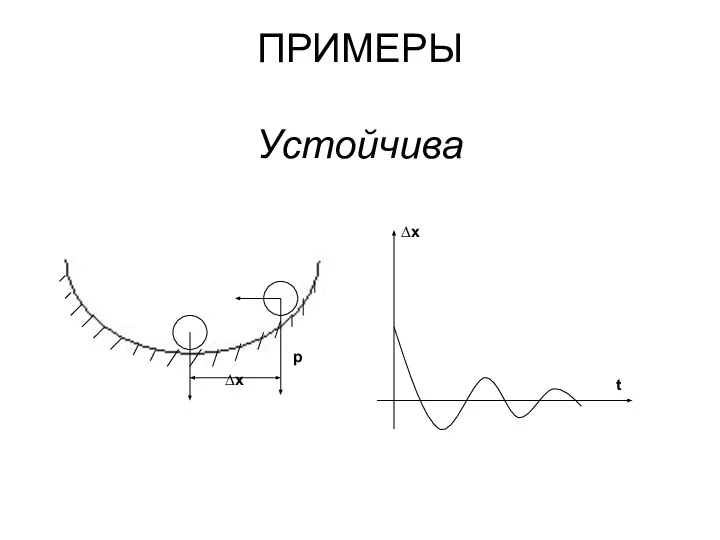
- 3. ПРИМЕРЫ Устойчива ∆х р
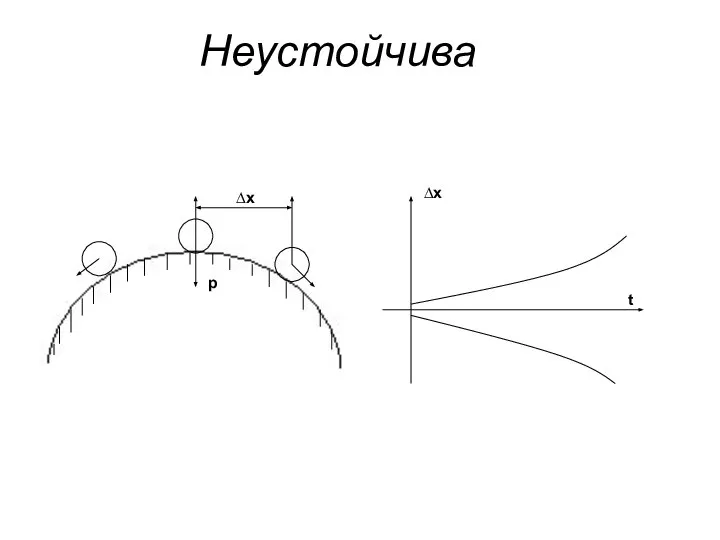
- 4. Неустойчива ∆х р ∆х
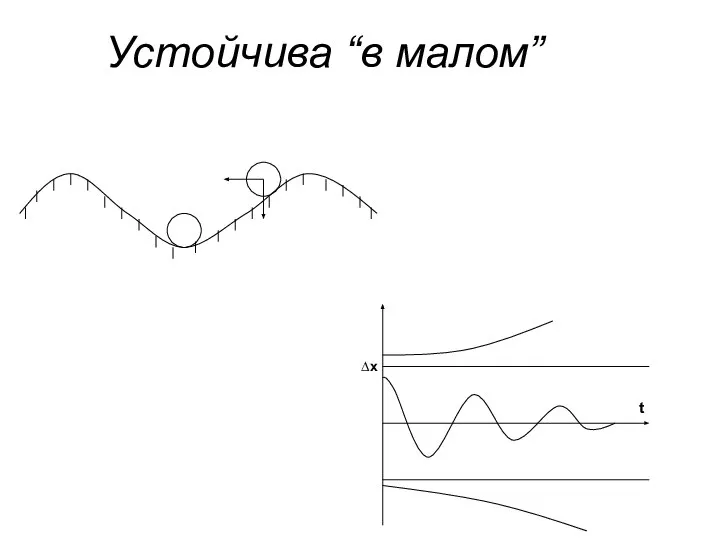
- 5. Устойчива “в малом”
- 6. Линейные САУ описываются линейными дифференциальными уравнениями (ДУ). Для решения ДУ следует найти корни его характеристического уравнения:
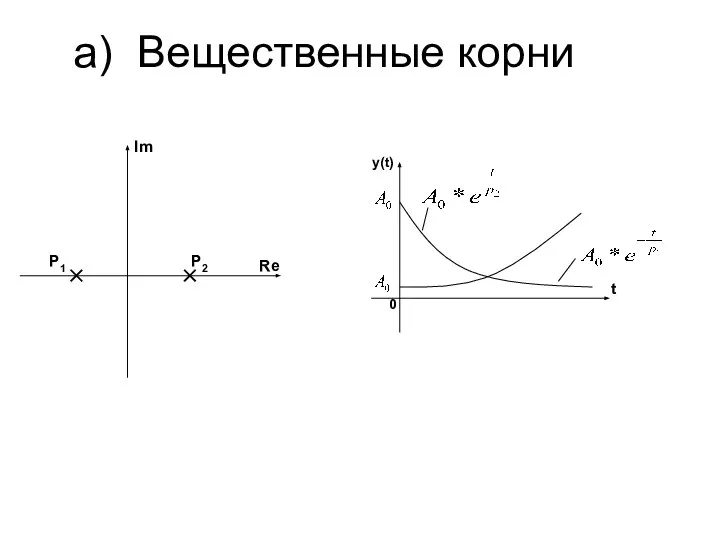
- 7. a) Вещественные корни
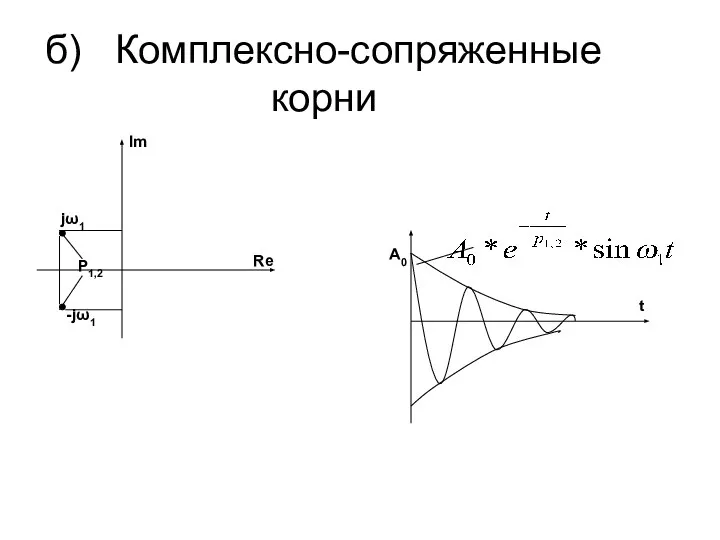
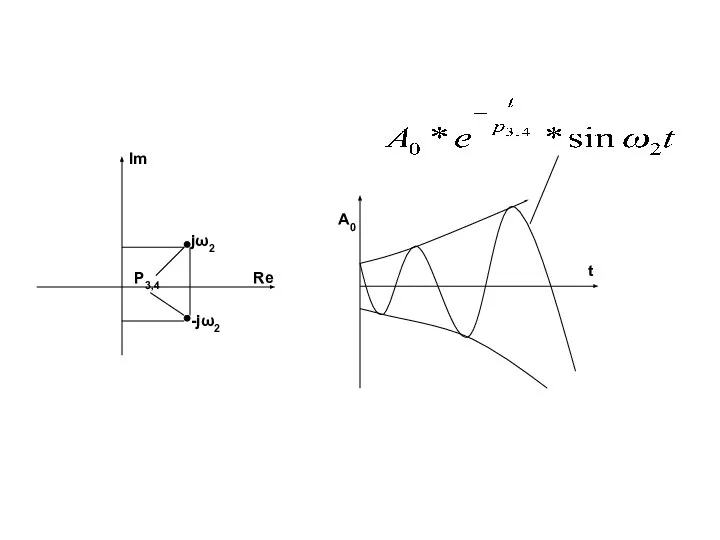
- 8. б) Комплексно-сопряженные корни
- 10. Итак, чтобы САУ была устойчивой необходимо и достаточно, чтобы все корни ее характеристического уравнения находились в
- 11. Критерии устойчивости САУ – это некоторые признаки позволяющие не решая характеристического уравнения оценить устойчивость САУ.
- 12. ВНИМАНИЕ Характеристическое уравнение замкнутой САУ – это знаменатель ее передаточной функции Ф(s) приравненный “0”. Характеристическое уравнение
- 13. А. Алгебраические критерии устойчивости САУ Критерий Гурвица (1895г.). Пусть дано ХУ замкнутой САУ anpn+an-1pn-1+…+a0=0 (1)
- 14. Составим определитель Гурвица из коэффициентов ХУ: ∆n= (2)
- 15. Как видно из (2): На главной диагонали определителя Гурвица располагаются сверху вниз коэффициенты ХУ начиная со
- 16. Составим главные диагональные миноры ∆1= an-1 ∆2 = ∆3=
- 17. 1. Критерий Гурвица: Для устойчивости линейной САУ необходимо и достаточно, чтобы при аn>0 все главные диагональные
- 18. Примеры 1. n=1 a1p+a0=0 Условия устойчивости a1>0 ∆1=a0>0 2. n=2 a2p2+a1p+a0=0 Условия устойчивости a2>0 ∆1=a1>0 ∆2=
- 19. 3. n=3 a3p3+a2p2+a1p=0 Условия устойчивости a3>0 ∆1=a2>0 ∆2 = =a2a1-a3a0>0 ∆3= =a0*∆2>0
- 20. Недостаток критерия Гурвица С увеличением “n” раскрывать определители становится трудно.
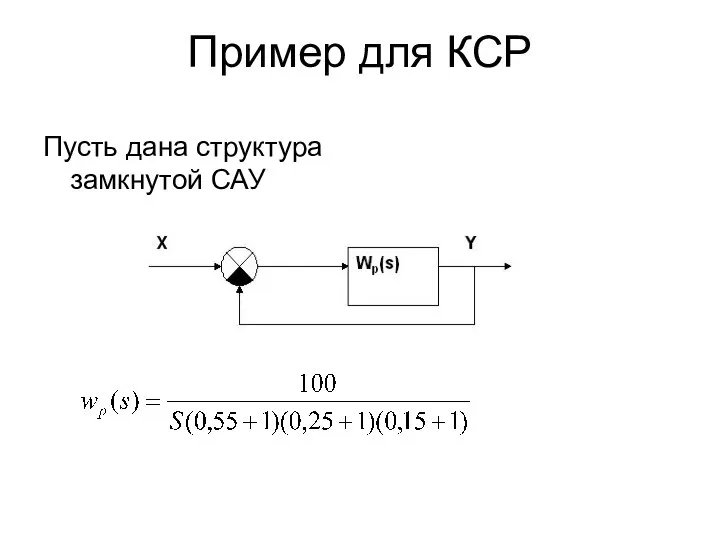
- 21. Пример для КСР Пусть дана структура замкнутой САУ
- 22. Необходимо с помощью критерия Гурвица определить устойчивость САУ. План исследований: 1. Найти передаточную функцию замкнутой САУ.
- 23. 2. Критерий Рауса Пусть дано ХУ замкнутой САУ “n”–го порядка: anpn + an-1pn-1 +… +a1p +
- 24. Составим таблицу Рауса из коэффициентов ХУ:
- 25. Критерий Рауса Для устойчивости линейной САУ необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса были
- 26. Пример I для КСР Пусть ХУ замкнутой САУ: P6 + 6p5 + 21p4 + 44p3 +
- 27. План исследования Составим таблицу Рауса и заполним ее первые две строки. Вычислим последовательно коэффициенты последующих строк.
- 28. Итак, составим таблицу Рауса
- 29. Задание по КСР: Завершить заполнение таблицы Рауса и оценить устойчивость САУ.
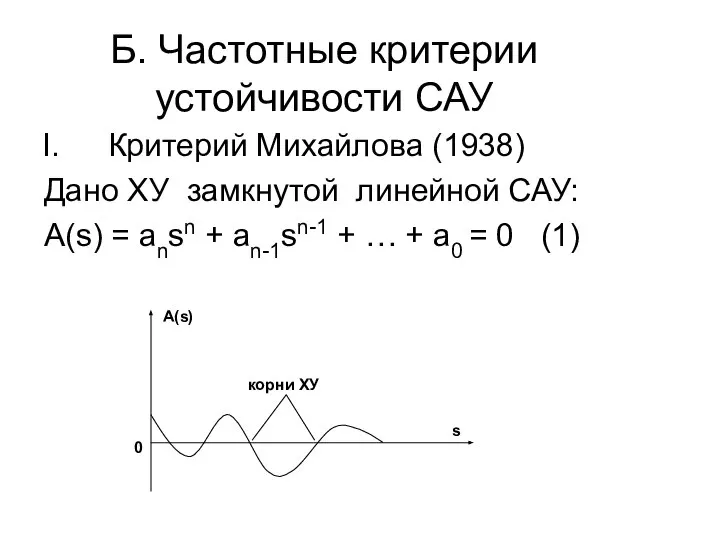
- 30. Б. Частотные критерии устойчивости САУ Критерий Михайлова (1938) Дано ХУ замкнутой линейной САУ: А(s) = ansn
- 31. Представим полином (1) в виде: A(s) = an (s – s1) (s –s2) … (s -
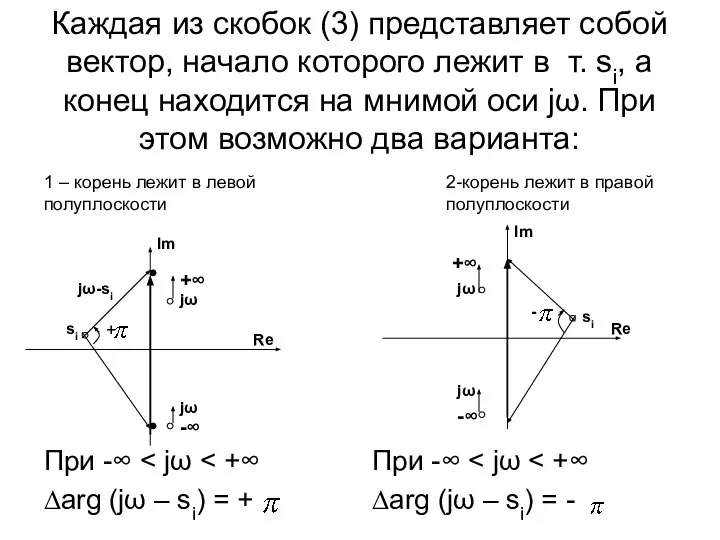
- 32. Каждая из скобок (3) представляет собой вектор, начало которого лежит в т. si, а конец находится
- 33. Итак, если ХУ A(s) = 0 содержит L корней в правой полуплоскости, то ∆arg A(jω) =
- 34. Для устойчивости линейной САУ необходимо, чтобы L = 0, т.е.: ∆arg A(jω) = n (4)
- 35. Критерий Михайлова является графической интерпретацией выражения (4). При этом рассматриваются лишь положительные частоты, т.е.: ∆arg A(jω)
- 36. Критерий Михайлова Для устойчивости линейной САУ необходимо и достаточно, чтобы годограф Михайлова (5) А(jω), начинаясь при
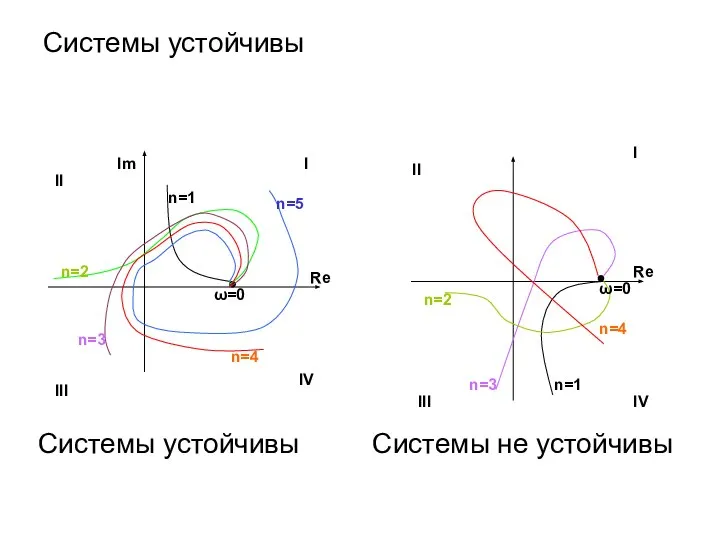
- 37. Системы устойчивы Системы устойчивы Системы не устойчивы
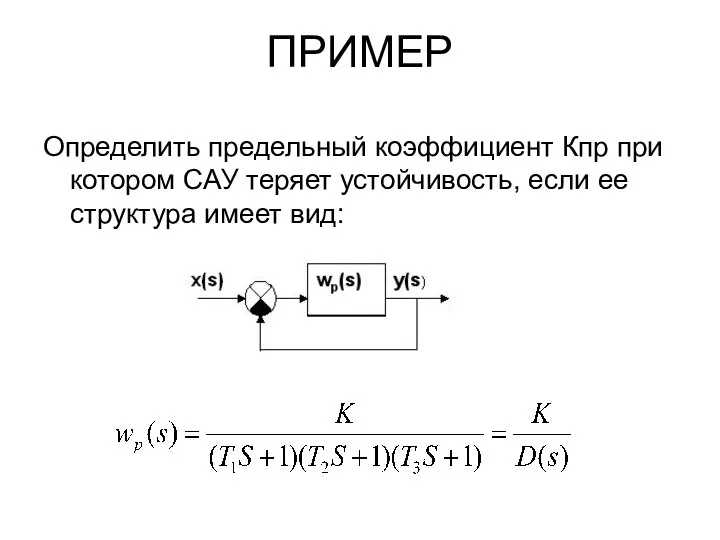
- 38. ПРИМЕР Определить предельный коэффициент Кпр при котором САУ теряет устойчивость, если ее структура имеет вид:
- 39. Найдем передаточную функцию замкнутой САУ: ХY САУ – это знаменатель ее передаточной функции приравненный к 0
- 40. 3. Годограф Михайлова (при s = jω): А(jω) =D(jω) + К 0 4. Построим, вначале, D(jω):
- 41. Кпр определим из уравнений Кпр определим из уравнений
- 42. НЕДОСТАТОК критерия Михайлова Годограф Михайлова не имеет физической сущности (его нельзя получить экспериментально). Между тем при
- 43. 2. Критерий Найквиста (1932) Основан на использовании wp(s), которую можно получить экспериментально. Пусть: - ПФ разомкнутой
- 44. Образуем функцию: - XY замкнутой САУ - XY разомкнутой САУ
- 45. РАССМОТРИМ 1-й случай – разомкнутая САУ устойчива. Тогда, согласно критерию Михайлова: ∆arg N(jω) = n* 0
- 46. Чтобы система и в замкнутом состоянии была устойчива необходимо чтобы: ∆arg 0 Это значит что: ∆arg
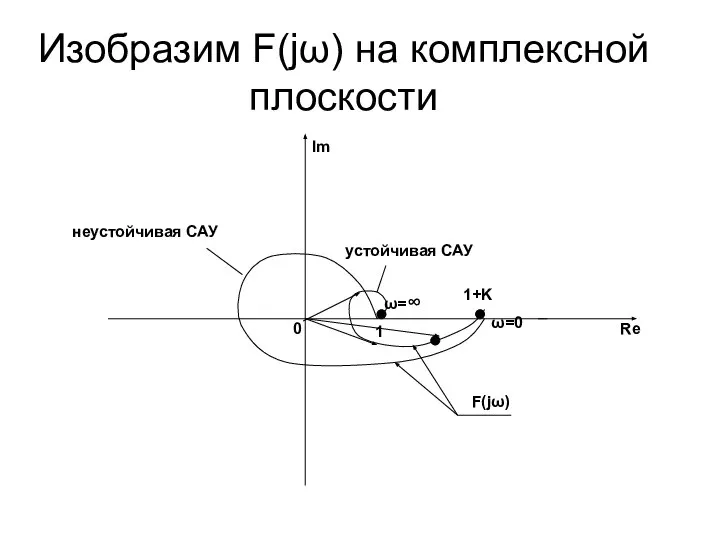
- 47. Изобразим F(jω) на комплексной плоскости
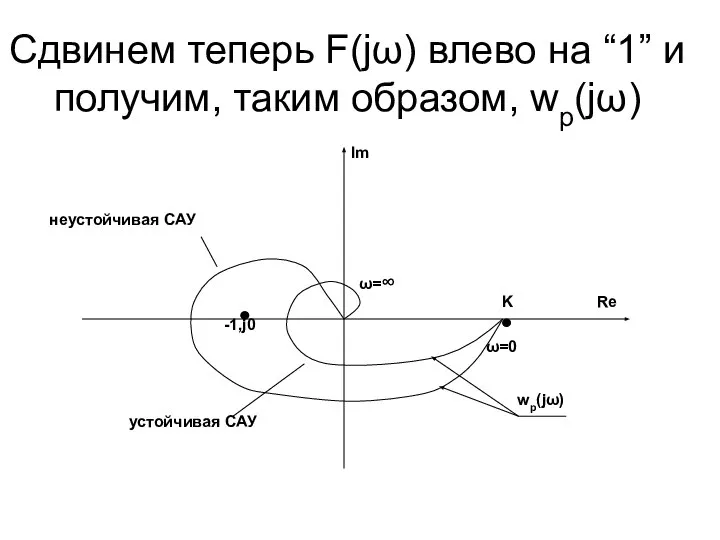
- 48. Сдвинем теперь F(jω) влево на “1” и получим, таким образом, wp(jω)
- 49. Критерий устойчивости Найквиста: Если разомкнутая САУ устойчива, то для ее устойчивости в замкнутом состоянии необходимо и
- 50. ПРИМЕР Найти, используя критерий Найквиста, предельный коэффициент Кпр при котором САУ потеряет устойчивость если:
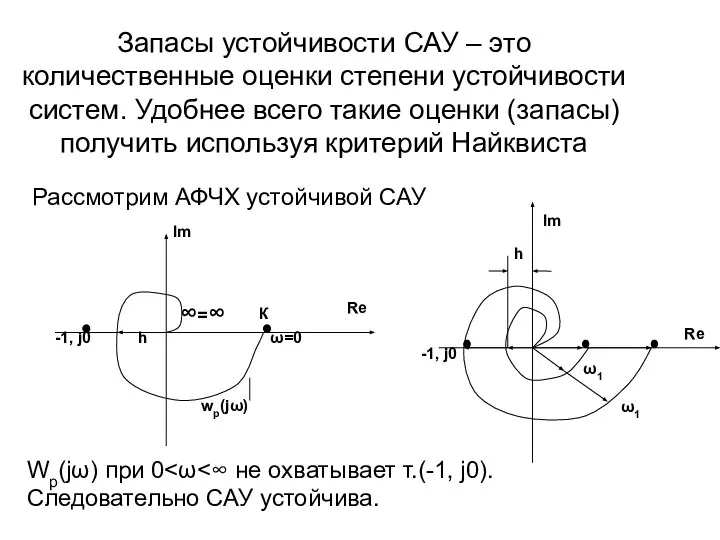
- 51. По критерию Найквиста САУ находится на границе устойчивости если: Полагая Im(ω ) = 0 найдем:
- 52. Подставив в Re(ω ) найдем: Т.е. результат такой же, как и при использовании критерия Михайлова.
- 53. Запасы устойчивости САУ – это количественные оценки степени устойчивости систем. Удобнее всего такие оценки (запасы) получить
- 54. САУ может потерять устойчивость по двум причинам: а) увеличения К без изменения фаз - все вектора
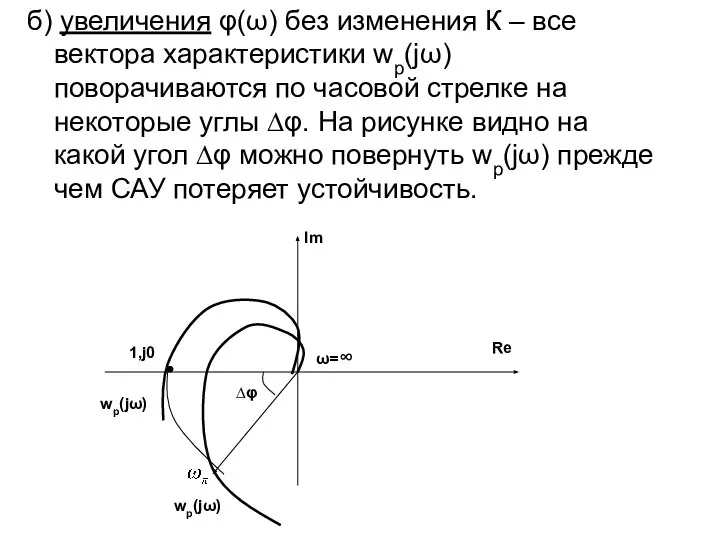
- 55. б) увеличения φ(ω) без изменения К – все вектора характеристики wp(jω) поворачиваются по часовой стрелке на
- 56. Проводя окружность радиусом “1” можно найти ту точку ω , которая попадет в точку (-1; j0)
- 57. Итак, существуют две количественные оценки степени устойчивости САУ Запас “по амплитуде” - ∆А= Запас “по фазе”
- 58. Анализ устойчивости САУ по логарифмическим характеристикам АФЧХ можно построить в логарифмическом масштабе в виде двух характеристик:
- 59. Тогда анализ устойчивости заметно упрощается. Особенно просто строятся т.н. асимптотические L(ω) – в виде кусочно-прямолинейных характеристик.
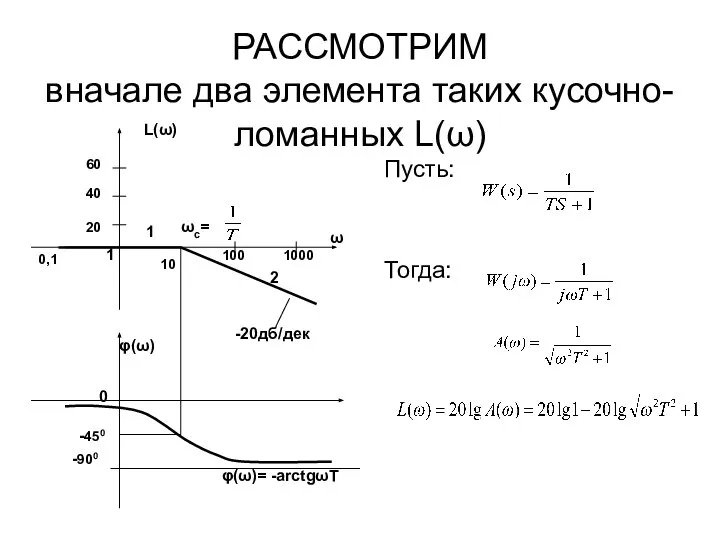
- 60. РАССМОТРИМ вначале два элемента таких кусочно-ломанных L(ω) Пусть: Тогда:
- 61. Пусть: Тогда:
- 62. Приближенно: при ω при ω > Итак L(ω) состоит из двух прямых (асимптот): 1 – совпадающей
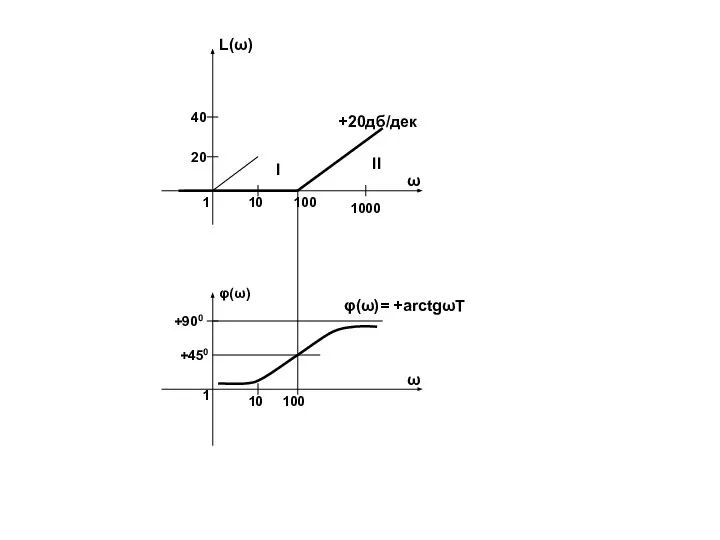
- 63. Частота ω = = ωс называется сопрягающей. На сопрягающей частота ωс = φ(ω) = - arctg1
- 64. Итак, чтобы построить L(ω) и φ(ω) для этого элемента – w(jω) = нужно: Найти сопрягающую частоту:
- 65. 4. По формуле φ(ω)= -arctgωT задаваясь разными частотами 0
- 66. Пусть теперь: Тогда: Приближенно: при ω при ω >
- 67. Т.О. и здесь L(ω) состоит из двух участков: 1 – вдоль оси ω до ω ≤
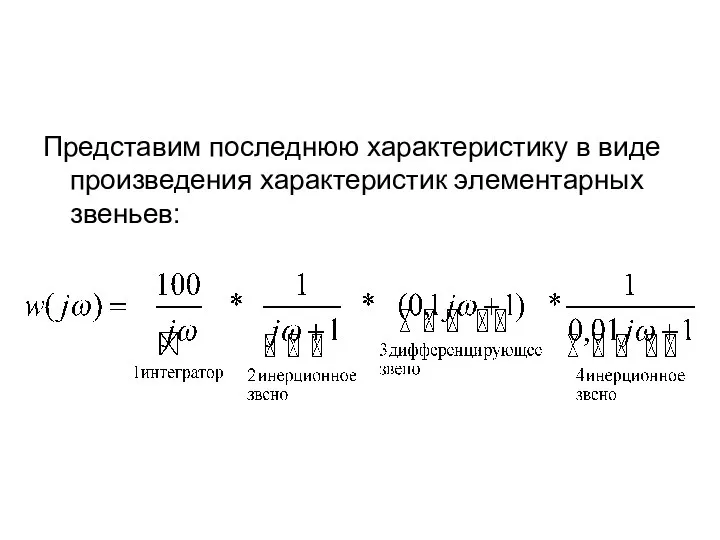
- 69. Построение асимптотических L(ω) и φ(ω) для сложных САУ. Пусть например: Заменив S→jω получим амплитудно-фазовые частотные характеристики:
- 70. Представим последнюю характеристику в виде произведения характеристик элементарных звеньев:
- 71. Определим сопрягающие частоты:
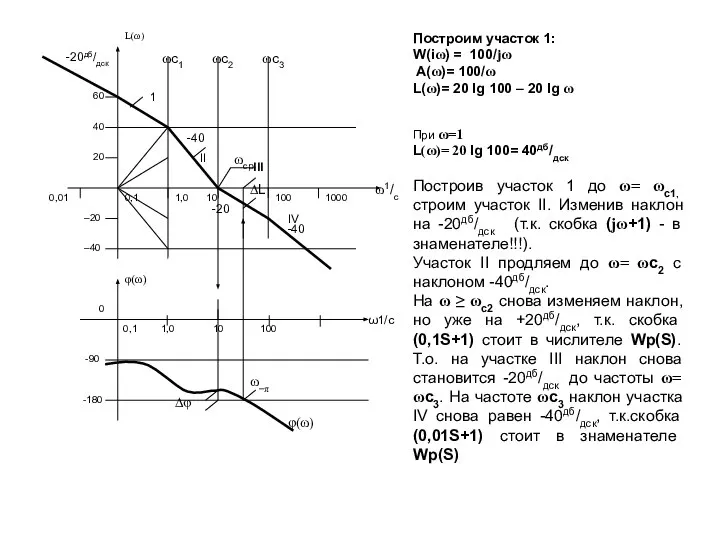
- 72. ω1/с Построим участок 1: W(iω) = 100/jω A(ω)= 100/ω L(ω)= 20 lg 100 – 20 lg
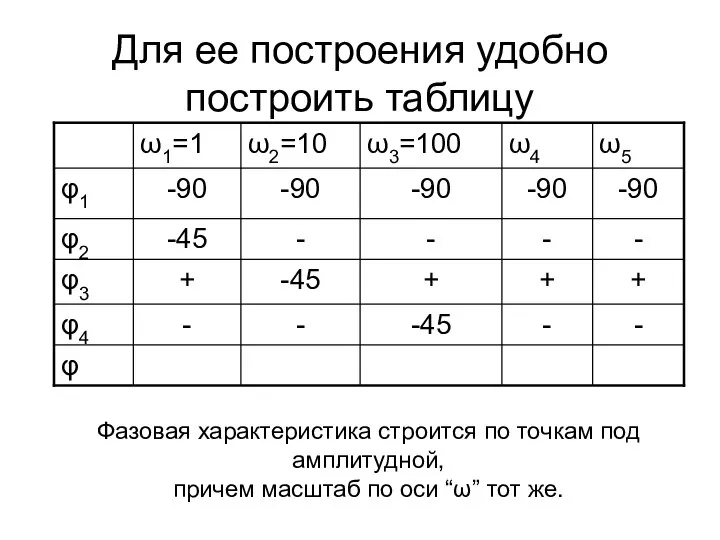
- 73. Фазовая характеристика φ(ω) САУ складывается из фазовых характеристик отдельных звеньев Wp(S): φ(ω) = –90°−(arctg1ω)+(arctg0,1ω) – (arctg0,01ω)
- 74. Для ее построения удобно построить таблицу Фазовая характеристика строится по точкам под амплитудной, причем масштаб по
- 75. Об устойчивости САУ судят по расположению точек пересечения L(ω) оси частот ωср –частота среза и φ(ω)
- 77. Скачать презентацию











































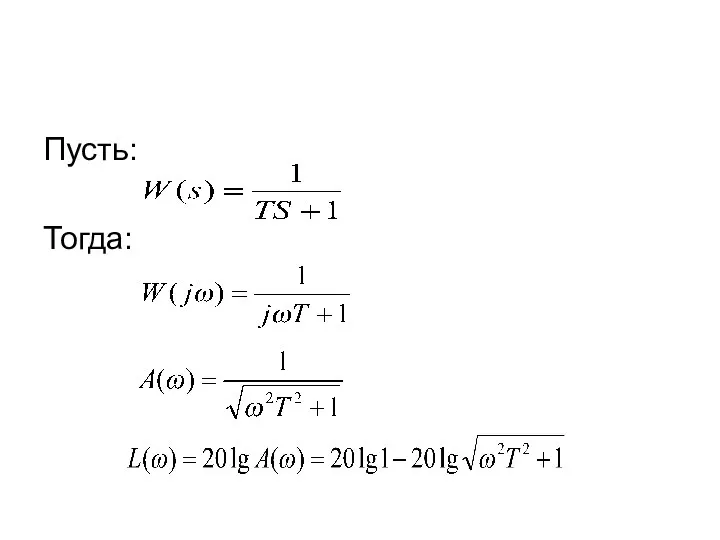










 Свойства некоторых аналоговых фильтров
Свойства некоторых аналоговых фильтров  ПРИОБРЕТЕНИЕ ПРАВА СОБСТВЕННОСТИ
ПРИОБРЕТЕНИЕ ПРАВА СОБСТВЕННОСТИ  Організація та проведення спортивних змагань
Організація та проведення спортивних змагань Моё хобби баскетбол
Моё хобби баскетбол АЛГОРИТМИ Й АЛГОРИТМІЗАЦІЯ
АЛГОРИТМИ Й АЛГОРИТМІЗАЦІЯ Кадровое обеспечение ИБ
Кадровое обеспечение ИБ Історичні відомості з розвитку геометричного різьблення
Історичні відомості з розвитку геометричного різьблення Лекция 3 Электропроводность растворов электролитов
Лекция 3 Электропроводность растворов электролитов Роль средств массовой информации в демократическом правовом государстве
Роль средств массовой информации в демократическом правовом государстве Категории обобщающих показателей
Категории обобщающих показателей Как подготовить проповедь или выступление на духовную тему
Как подготовить проповедь или выступление на духовную тему Функциональная анатомия конечного мозга
Функциональная анатомия конечного мозга  Щитовидная железа
Щитовидная железа  Макроэкономические показатели (система национальных счетов) ВВП и его структура
Макроэкономические показатели (система национальных счетов) ВВП и его структура Основы технической механики. Основы статики. Урок 1
Основы технической механики. Основы статики. Урок 1 Моё хобби «Бабочки»
Моё хобби «Бабочки» Символизм литературно – художественное направление конца XIX - начала XX века. Первое и самое значительное из модернистских тече
Символизм литературно – художественное направление конца XIX - начала XX века. Первое и самое значительное из модернистских тече Антиангинальные и антигипертензивные средства
Антиангинальные и антигипертензивные средства Скоморохи на Древней Руси
Скоморохи на Древней Руси Резонанс
Резонанс Законность и правопорядок
Законность и правопорядок Инструментальные средства информационных технологий
Инструментальные средства информационных технологий Непрерывная интеграция Андрей Дзыня. Lohika Systems Kyiv
Непрерывная интеграция Андрей Дзыня. Lohika Systems Kyiv По данным различных исследователей количество детей с трудностями в обучении в дошкольном возрасте достигает до 25%,
По данным различных исследователей количество детей с трудностями в обучении в дошкольном возрасте достигает до 25%,  Выполнила студентка 2-ого курса Факультета иностранных языков Группы АФ 21/2 Лисейцева Дарья «Использование Интернета на занятиях п
Выполнила студентка 2-ого курса Факультета иностранных языков Группы АФ 21/2 Лисейцева Дарья «Использование Интернета на занятиях п Стратегия и тактика избирательной кампании. (Лекция 14)
Стратегия и тактика избирательной кампании. (Лекция 14) Програмування мікроконтролерів. Лекція 1. Базові поняття програмування мікроконтролерів. Бібліотеки CMSIS і SPL
Програмування мікроконтролерів. Лекція 1. Базові поняття програмування мікроконтролерів. Бібліотеки CMSIS і SPL Поликонденсационные смолы и пластмассы на их основе
Поликонденсационные смолы и пластмассы на их основе