Содержание
- 2. В широком смысле общая задача оптимизации параметров систем автоматизации заключается в поиске экстремума критерия (целевой функции)
- 3. Основные методы решения задач оптимизации Математическое программирование Линейное программирование Нелинейное программирование Дискретное программирование Для решения большинства
- 4. Двоичные переменные Задачи с дискретными переменными Задача стохастического программирования Детерминированный эквивалент стохастической задачи Оптимизация при недетерминированных
- 5. Данный метод решает задачи, в которых искомые переменные могут принимать не любые целые значения, а только
- 6. Если в оптимальное решение должен входить один из двух вариантов, то сумма переменных: Если в оптимальное
- 7. Этот метод используется для решения оптимизационных задач со случайной исходной информацией. Например, мощности нагрузок в системе
- 8. Пре решении оптимизационных задач все искомые переменные или их часть должны принимать только значения целых чисел.
- 9. Целочисленная переменная x имеет 4 значения (x=0,1,2,3), а непрерывная переменная – бесконечное количество. Поэтому, попытка решить
- 10. В ряде практических оптимизационных задач заранее известен набор допустимых решений, из которых требуется выбрать оптимальное решение.
- 11. Составить математическую модель для определения в схеме электроснабжения оптимального узла установки компенсирующего устройства, заданной мощности. Критерий
- 12. Решение 1. Обозначим переменнымиQk1,Qk2 и Qk3 мощности компенсирующих устройств. Это дискретные переменные, каждая из которых может
- 13. 5. Величина дискретной переменной Qki будет зависеть от значения соответствующей двоичной переменной δi. Переменная Qki =Qk
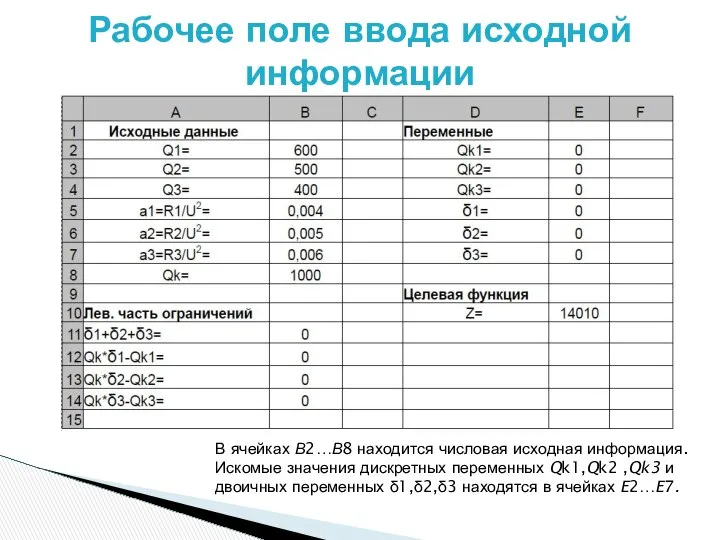
- 14. Рабочее поле ввода исходной информации В ячейках В2…В8 находится числовая исходная информация. Искомые значения дискретных переменных
- 15. Целевая функция задачи где: a1 = R1/U^2 = 0.004; a2 = R2/U^2 = 0.005; a3 =
- 16. В диалоговом окне «Поиск решения»: устанавливается адрес ячейки целевой функции Е10; отмечается, что ищется минимальное значение
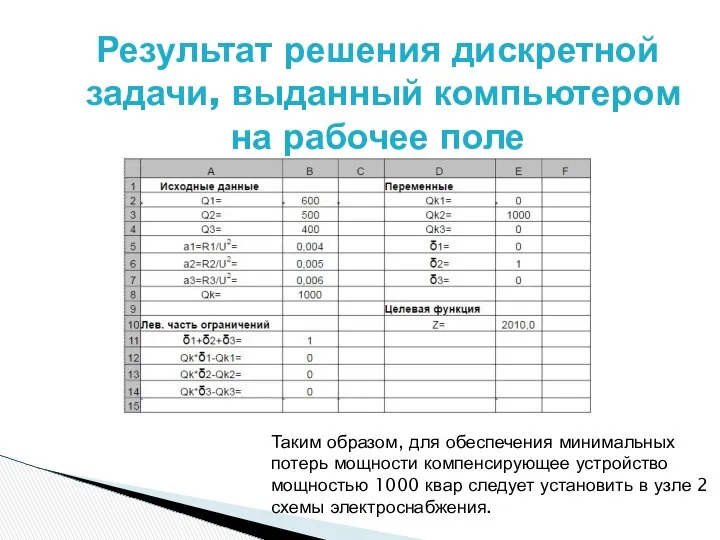
- 17. Результат решения дискретной задачи, выданный компьютером на рабочее поле Таким образом, для обеспечения минимальных потерь мощности
- 19. Скачать презентацию














 Презентация "Путешествие от барокко к классицизму 1" - скачать презентации по МХК
Презентация "Путешествие от барокко к классицизму 1" - скачать презентации по МХК Европейские строительные стандарты
Европейские строительные стандарты Общество ждет от выпускника школы ясного выбора сферы профессиональной деятельности . Ожидания закономерно связываются с профили
Общество ждет от выпускника школы ясного выбора сферы профессиональной деятельности . Ожидания закономерно связываются с профили Идеи основателей геополитики
Идеи основателей геополитики Заболевания сосуд.тракта (увеиты)
Заболевания сосуд.тракта (увеиты)  Ремонт дома после пожара
Ремонт дома после пожара Взаимосвязь между Р-Т, Т-Х и P-Х проекциями
Взаимосвязь между Р-Т, Т-Х и P-Х проекциями Изменение имён прилагательных по родам Презентация к уроку русского языка в 3 классе УМК «Школа России» Автор: Неделина Наталья В
Изменение имён прилагательных по родам Презентация к уроку русского языка в 3 классе УМК «Школа России» Автор: Неделина Наталья В Средний уровень цен. Инфляция
Средний уровень цен. Инфляция Толерантность в школе
Толерантность в школе Обзорно-сравнительные радионавигационные системы (корреляционно-экстремальная система)
Обзорно-сравнительные радионавигационные системы (корреляционно-экстремальная система) БРЮШНОЙ ТИФ. ШИГЕЛЛЕЗ. ПИЩЕВЫЕ ТОКСИКОИНФЕКЦИИ. САЛЬМОНЕЛЛЕЗ. БОТУЛИЗМ. ХОЛЕРА
БРЮШНОЙ ТИФ. ШИГЕЛЛЕЗ. ПИЩЕВЫЕ ТОКСИКОИНФЕКЦИИ. САЛЬМОНЕЛЛЕЗ. БОТУЛИЗМ. ХОЛЕРА  6. Java basic I/O 4. Networking
6. Java basic I/O 4. Networking НовАТранс НТС Камышлов
НовАТранс НТС Камышлов Спортивная площадка «Стартуем вместе»
Спортивная площадка «Стартуем вместе» Хронический пульпит у детей
Хронический пульпит у детей  Юбилейная 70-ая Международная научная конференция «Нефть и газ-2016»
Юбилейная 70-ая Международная научная конференция «Нефть и газ-2016» Защита информации
Защита информации  Судебные споры, банкротство и субсидиарная ответственность в финансовом секторе
Судебные споры, банкротство и субсидиарная ответственность в финансовом секторе Византийские мозаики
Византийские мозаики Презентация на тему "Синергические и антагонистические эффекты при комбинированных воздействиях: новые данные и перспективы&quo
Презентация на тему "Синергические и антагонистические эффекты при комбинированных воздействиях: новые данные и перспективы&quo Презентация Продовольственная и сельскохозяйственная организация
Презентация Продовольственная и сельскохозяйственная организация  Сравнение C и C++
Сравнение C и C++ ХЕЛИКОБАКТЕРИОЗЫ СПбГУ 2015г.
ХЕЛИКОБАКТЕРИОЗЫ СПбГУ 2015г.  Морфологиялық тұтастық белгісі
Морфологиялық тұтастық белгісі Разработка дизайна арт объекта для IT-организации
Разработка дизайна арт объекта для IT-организации Предмет и задачи патофизиологии
Предмет и задачи патофизиологии Спешите делать добро Классный руководитель: Варанкина Любовь Ивановна
Спешите делать добро Классный руководитель: Варанкина Любовь Ивановна