Содержание
- 2. | Ψ 〉(t) = C1(t)| 1 〉 + C2(t)| 2 〉 + … + Cn(t)| n
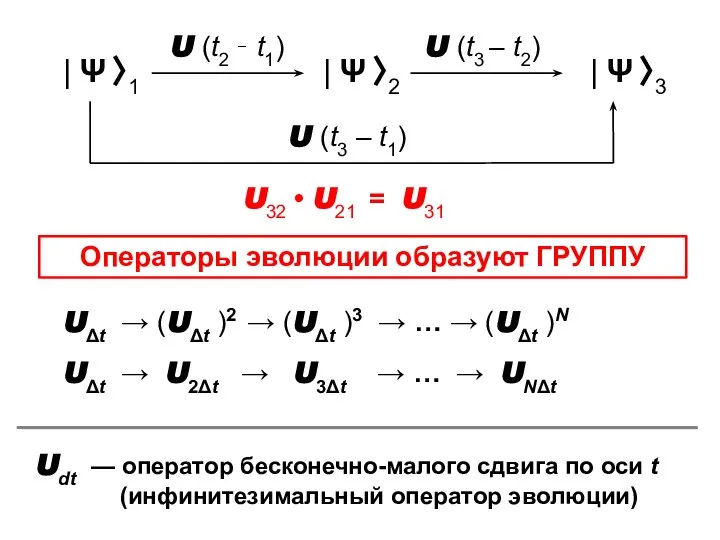
- 3. Оператор эволюции
- 4. U32 • U21 = U31 Операторы эволюции образуют ГРУППУ UΔt → (UΔt )2 → (UΔt )3
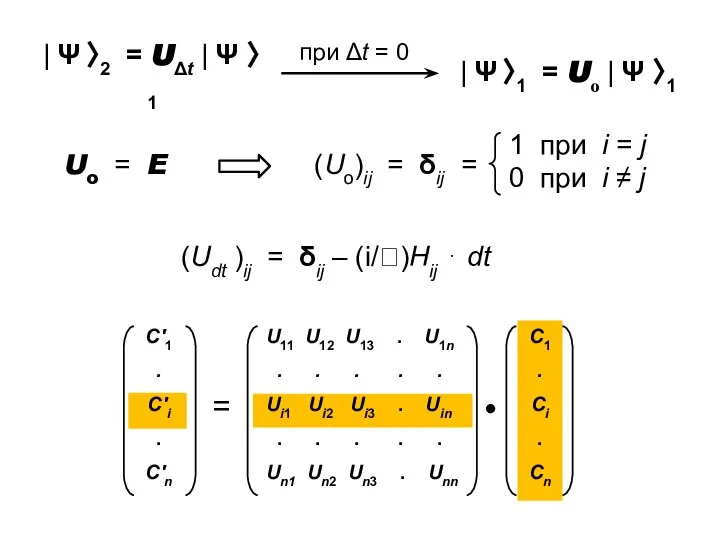
- 5. Матричное представление операторов эволюции UΔt = ( Uij ) Uij = f ( t ) UΔt
- 6. (Udt )ij = δij – (i/)Hij ⋅ dt
- 7. C'i = ∑ Uij ⋅ Cj = ∑ [δij – (i/)Hij ⋅ dt] ⋅ Cj =
- 8. Уравнение Шредингера H — оператор Гамильтона (гамильтониан)
- 9. Ψ(t + dt) = Ψ(t) + d Ψ = Ψ(t) – (i/)[H Ψ(t)]dt Оператор Гамильтона Н|
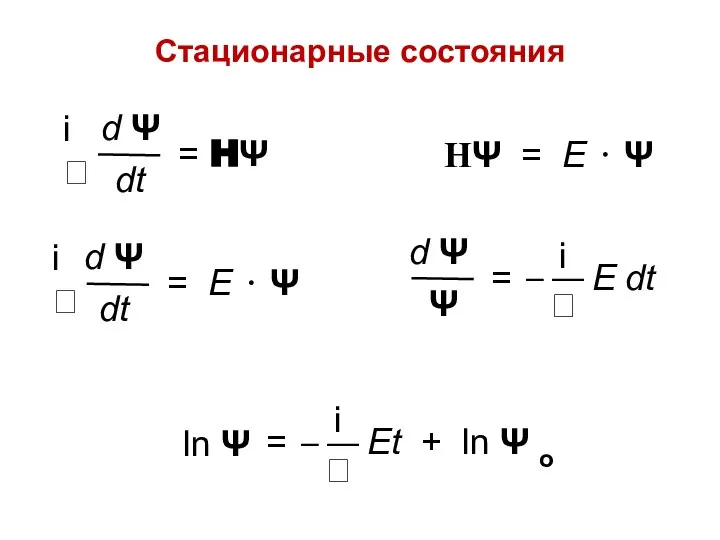
- 10. Стационарные состояния НΨ = Е ⋅ Ψ
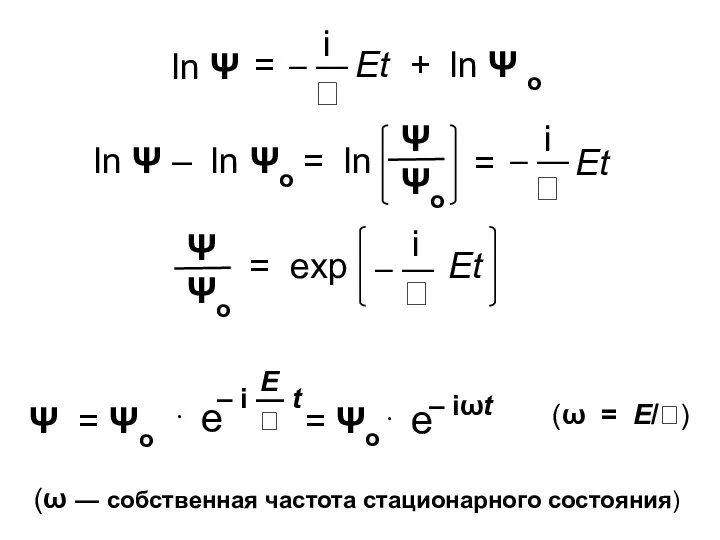
- 11. (ω = E/) (ω — собственная частота стационарного состояния)
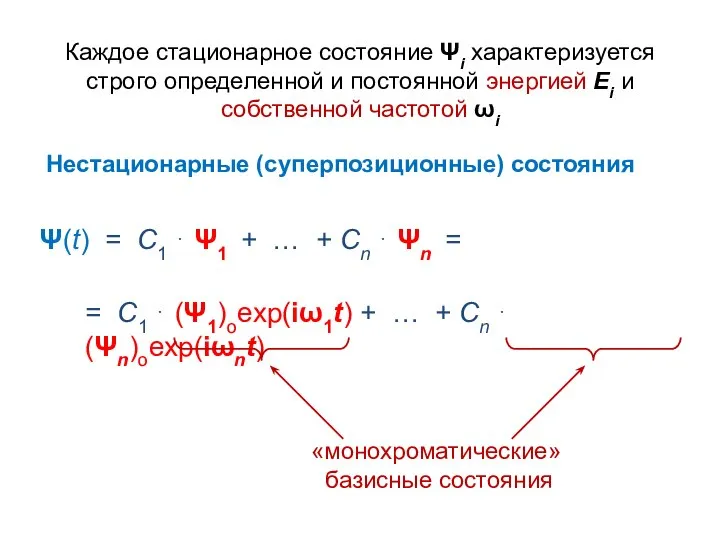
- 12. Каждое стационарное состояние Ψi характеризуется cтрого определенной и постоянной энергией Еi и собственной частотой ωi Нестационарные
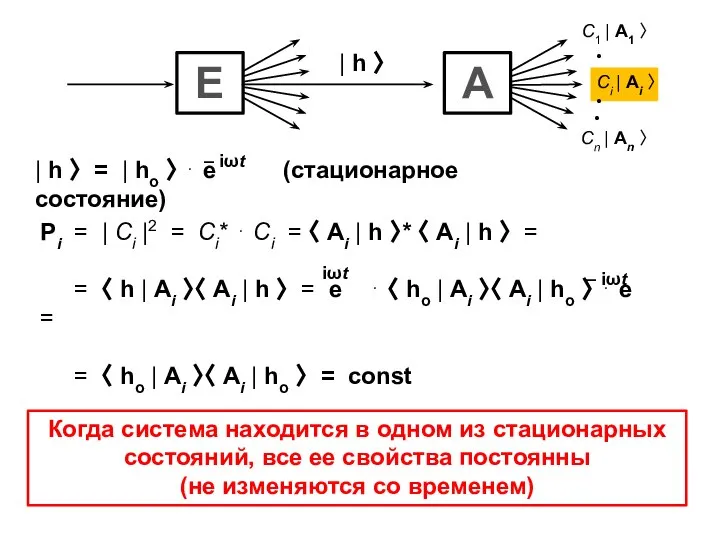
- 13. Когда система находится в одном из стационарных состояний, все ее свойства постоянны (не изменяются со временем)
- 14. любая собственная функция (собственный вектор) гамильтониана описывает стационарное состояние, стационарное состояние обязательно монохроматическое и имеет строго
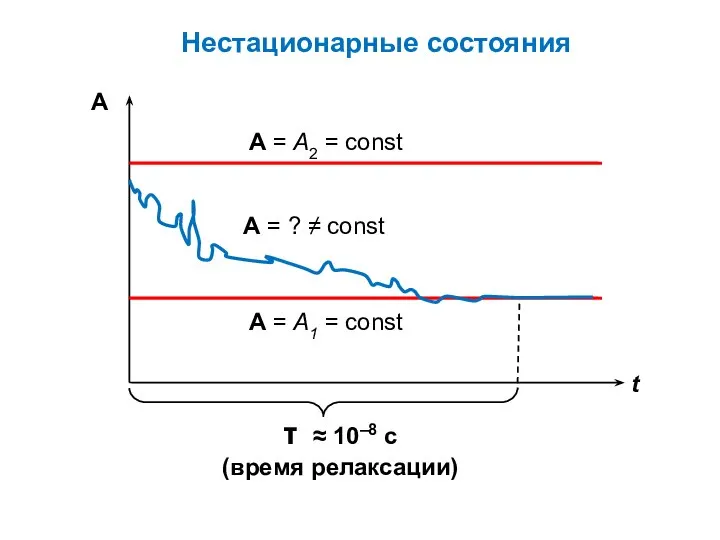
- 15. Нестационарные состояния
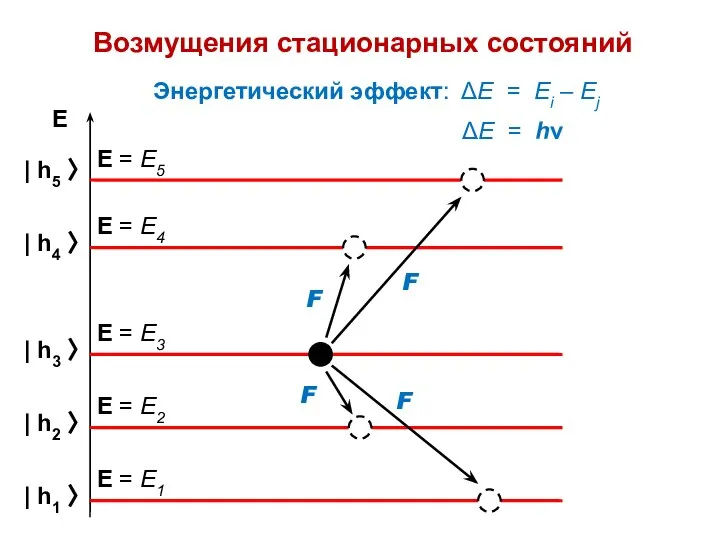
- 16. Возмущения стационарных состояний Энергетический эффект: ΔЕ = Ei – Ej ΔЕ = hν
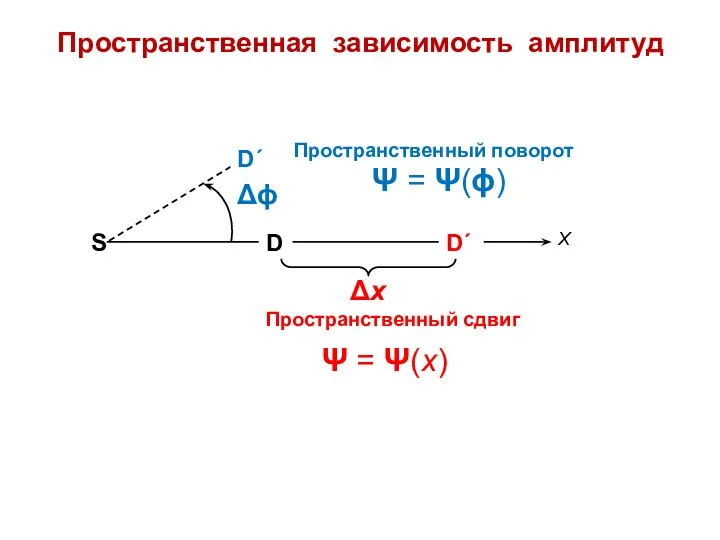
- 17. Пространственная зависимость амплитуд
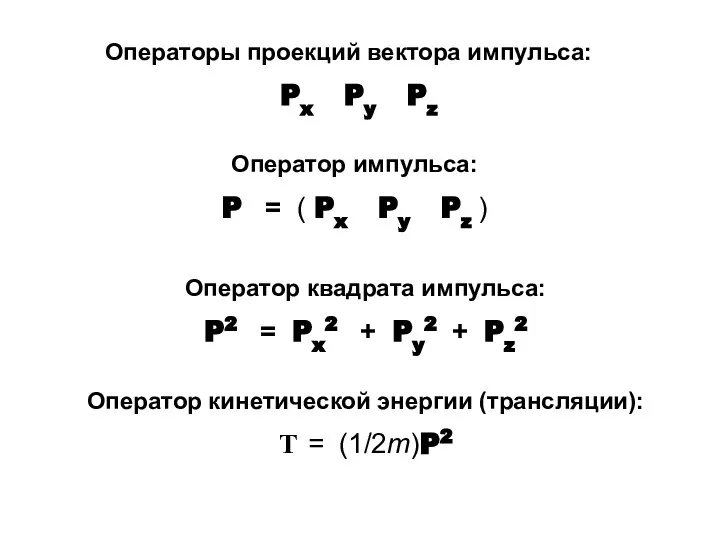
- 19. Оператор кинетической энергии (трансляции): Т = (1/2m)P2
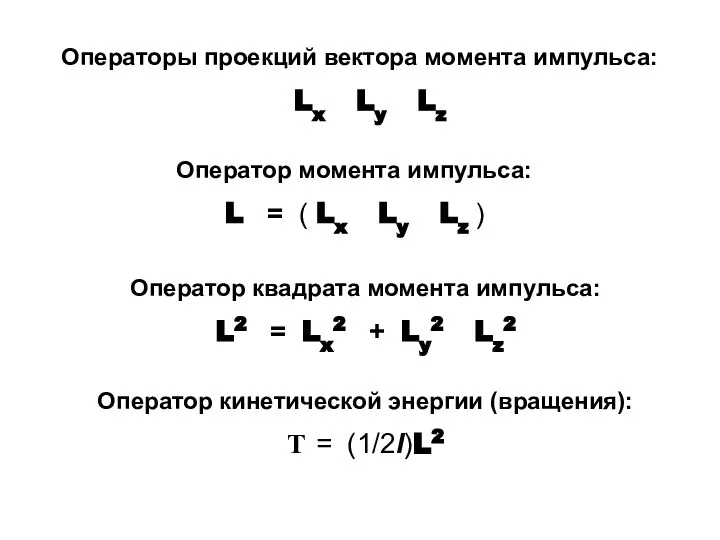
- 20. Оператор кинетической энергии (вращения): Т = (1/2I)L2
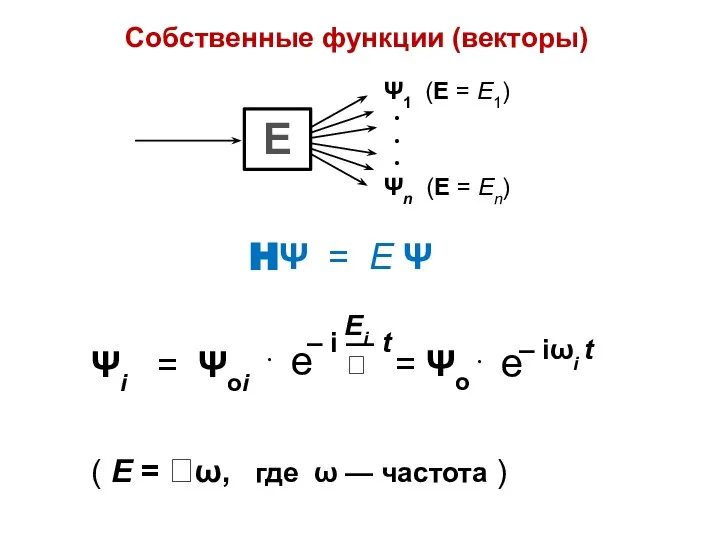
- 21. HΨ = E Ψ Собственные функции (векторы) ( E = ω, где ω — частота )
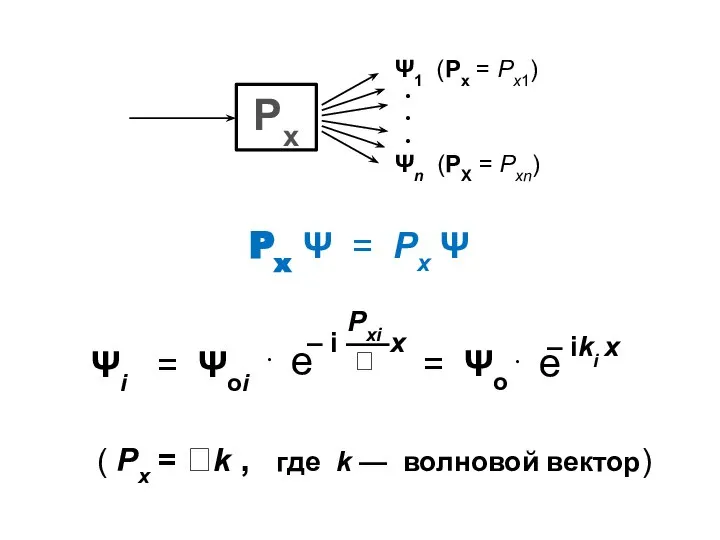
- 22. Px Ψ = Px Ψ ( Px = k , где k — волновой вектор)
- 24. Скачать презентацию



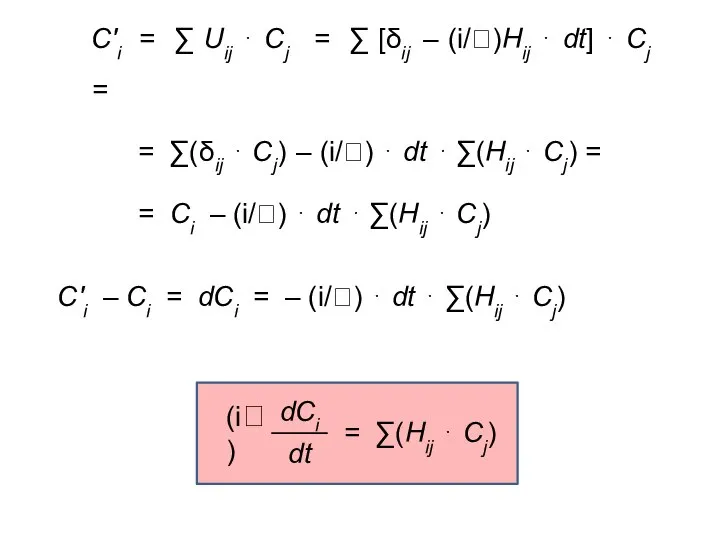




 Совет Школы МОУ Ундино –Посельской СОШ Председатель СШ Лаврентьева С.А. Секретарь СШ Гордеева М.К Члены
Совет Школы МОУ Ундино –Посельской СОШ Председатель СШ Лаврентьева С.А. Секретарь СШ Гордеева М.К Члены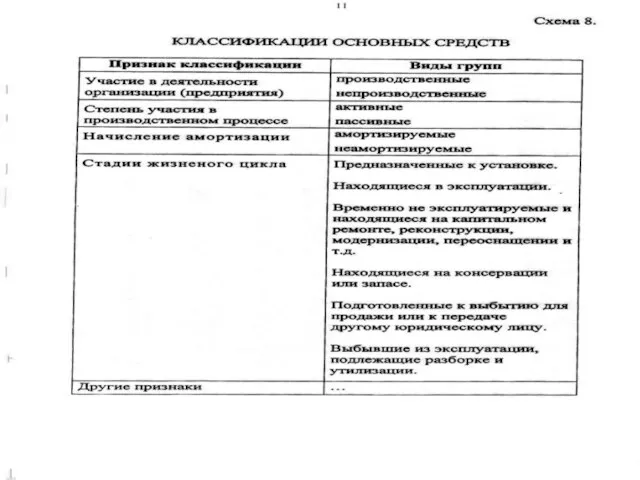 Презентация Основные средства предприятия
Презентация Основные средства предприятия Правила разработки, оформления и выпуска конструкторской документации
Правила разработки, оформления и выпуска конструкторской документации Олимпийские игры
Олимпийские игры Презентация Н.А. Бердяев о демократии, свободе личности, тоталитаризме
Презентация Н.А. Бердяев о демократии, свободе личности, тоталитаризме Политика гласности при Горбачёве
Политика гласности при Горбачёве Методика составления комплексов упражнений в различных видах производственной гимнастики и определение их места в течение дня
Методика составления комплексов упражнений в различных видах производственной гимнастики и определение их места в течение дня Цикл уроков для 9 класса Последовательности (можно ли объять необъятное…) Учитель – Закуцкая М.В. ГОУ лицей 179 2010 – 2011 уч.г. - презентация
Цикл уроков для 9 класса Последовательности (можно ли объять необъятное…) Учитель – Закуцкая М.В. ГОУ лицей 179 2010 – 2011 уч.г. - презентация Аналоговые и цифровые сигналы
Аналоговые и цифровые сигналы Презентация Деловые переговоры
Презентация Деловые переговоры Презентация на тему "Оплодотворение и развитие зародыша" - скачать презентации по Биологии
Презентация на тему "Оплодотворение и развитие зародыша" - скачать презентации по Биологии Архитектура ампир: торжественность, монументальность, симметричность композиции
Архитектура ампир: торжественность, монументальность, симметричность композиции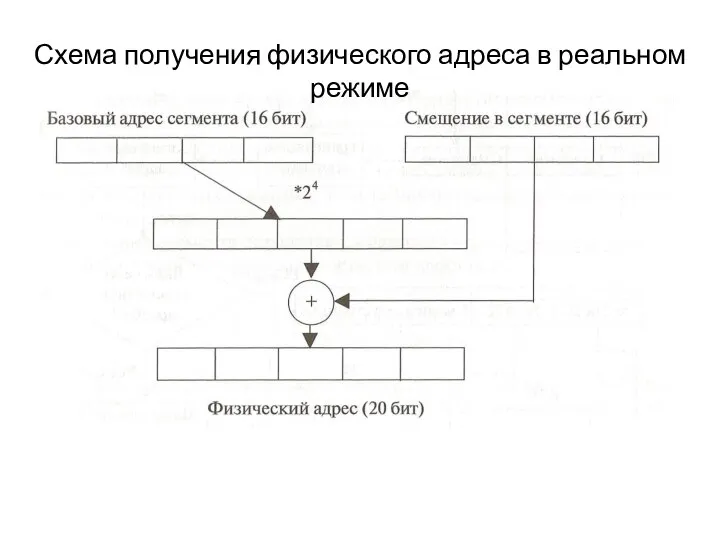 Схема получения физического адреса в реальном режиме
Схема получения физического адреса в реальном режиме Презентация Инновационное развитие Китая
Презентация Инновационное развитие Китая Увлекательная астрономия - презентация для начальной школы
Увлекательная астрономия - презентация для начальной школы Презентация на тему «Иконы»
Презентация на тему «Иконы»  «Д. И. Менделеев. Толковый тариф, или Исследование о развитии промышленности России в связи с ее общим таможенным тарифом 1891г.» Вып
«Д. И. Менделеев. Толковый тариф, или Исследование о развитии промышленности России в связи с ее общим таможенным тарифом 1891г.» Вып Техники плавания
Техники плавания Презентация Денежно-кредитная политика ЦБ
Презентация Денежно-кредитная политика ЦБ Теория государства и права и сравнительное правоведение
Теория государства и права и сравнительное правоведение Management in Russia
Management in Russia Понятие и признаки правонарушений
Понятие и признаки правонарушений Мікропроцесорне керування світловими пристроями
Мікропроцесорне керування світловими пристроями Первичное исследование. Ищем новые аудитории через ТаргетХантер
Первичное исследование. Ищем новые аудитории через ТаргетХантер Китайская кухня
Китайская кухня Юридический конфликт: сущность, динамика, типология
Юридический конфликт: сущность, динамика, типология  Необычные памятники. Памятники мебели и предметам обихода.
Необычные памятники. Памятники мебели и предметам обихода. Вязание узлов в альпинизме
Вязание узлов в альпинизме