Содержание
- 2. Формулировки второго начала термодинамики Второе начало термодинамики определяет условия, при которых возможны превращения энергии, описывающиеся уравнением
- 3. Другой вид формулировки второго начала термодинамики по Кельвину Вечный двигатель второго рода невозможен, т.е. невозможно создать
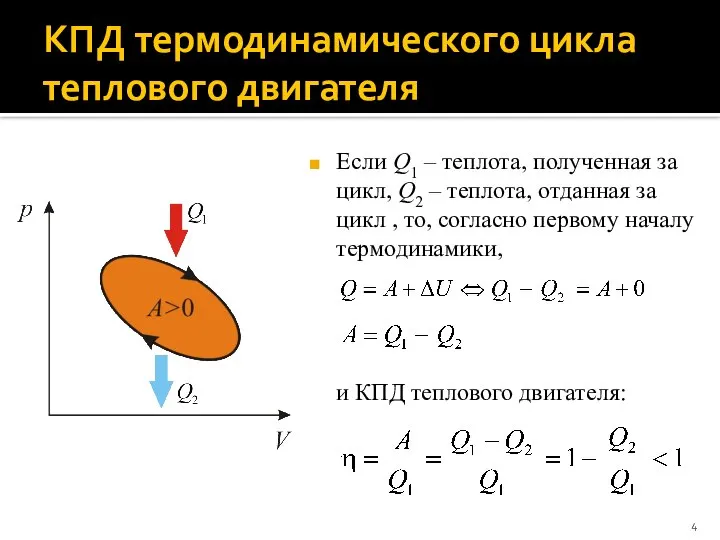
- 4. КПД термодинамического цикла теплового двигателя Если Q1 – теплота, полученная за цикл, Q2 – теплота, отданная
- 5. КПД термоднамического цикла холодильной машины Холодильная машина отбирает у тела с температурой T2 теплоту Q2 и
- 6. 4.2 Обратимые и необратимые процессы. Энтропия системы ЛЕКЦИЯ 4. ВТОРОЕ И ТРЕТЬЕ НАЧАЛА ТЕРМОДИНАМИКИ
- 7. Обратимость процессов в механике Простые механические движения всегда обратимы. Например: колебания математического маятника; упругое соударение тел.
- 8. Пример необратимого процесса: движение пули в воздухе
- 9. Вопрос об обратимости процессов в термодинамике Нельзя ли с помощью каких-либо процессов или механизмов добиться того,
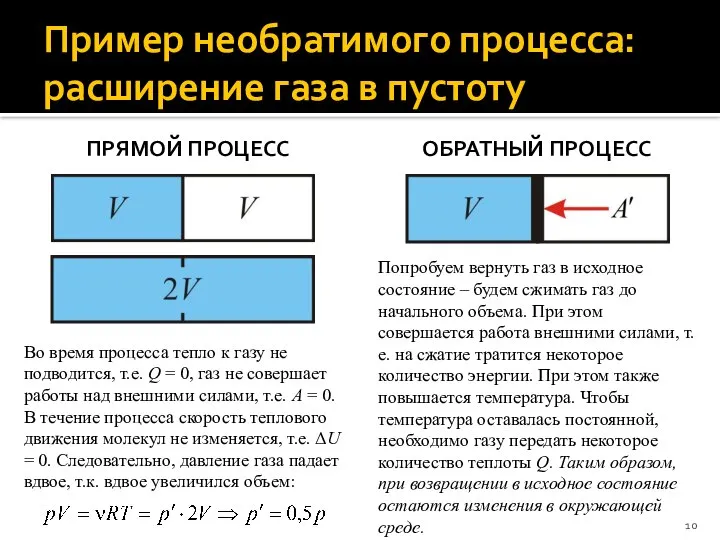
- 10. Пример необратимого процесса: расширение газа в пустоту ПРЯМОЙ ПРОЦЕСС ОБРАТНЫЙ ПРОЦЕСС Во время процесса тепло к
- 11. Пример обратимого термодинамического процесса: адиабатический процесс При адиабатическом процессе нет теплообмена с окружающей средой, т.е. Q
- 12. Пример обратимого термодинамического процесса: изотермическое сжатие При изотермическом сжатии температура газа остается постоянной, равной температуре окружающей
- 13. Квазистатические процессы Квазистатический процесс – это процесс, текущий бесконечно медленно и представляющий собой бесконечную последовательность равновесных
- 14. Энтропия В термодинамике энтропия вводится через элементарное приращение: и является полным дифференциалом, т.е. функцией состояния системы
- 15. Свойства энтропии 1. Энтропия – функция состояния. Если процесс производят вдоль адиабаты, то энтропия системы не
- 16. Свойства энтропии 2. Энтропия – величина аддитивная: энтропия макросистемы равна сумме энтропий ее частей. 3. Принцип
- 17. Изменение энтропии и процессы в природе Все самопроизвольно протекающие процессы в природе – от теплообмена до
- 18. Теорема Нернста Эта теорема утверждает, что при приближении температуры к абсолютному нулю энтропия системы также стремится
- 19. 4.3 Вычисление энтропии. Основное уравнение термодинамики ЛЕКЦИЯ 4. ВТОРОЕ И ТРЕТЬЕ НАЧАЛА ТЕРМОДИНАМИКИ
- 20. Основное уравнение термодинамики Оно представляет собой объединение первого начала термодинамики и выражения для элементарного приращения энтропии.
- 21. Энтропия идеального газа Пусть начальное 1 и конечное 2 состояния идеального газа характеризуются параметрами p1, V1
- 22. Энтропия идеального газа Подставим это выражение в уравнение для элементарного приращения энтропии: Интегрируя обе части данного
- 23. Приращение энтропии в необратимом процессе Непосредственно считать изменение энтропии в каком-либо необратимом процессе невозможно. Однако, энтропия
- 24. Возрастание энтропии при смешении газов После необратимого процесса смешения газов система перейдем в равновесное состояние, при
- 25. Парадокс Гиббса Последняя формулы приводит к выводу, называемому парадоксом Гиббса: Допустим, что газы 1 и 2
- 26. 4.4 Цикл Карно ЛЕКЦИЯ 4. ВТОРОЕ И ТРЕТЬЕ НАЧАЛА ТЕРМОДИНАМИКИ
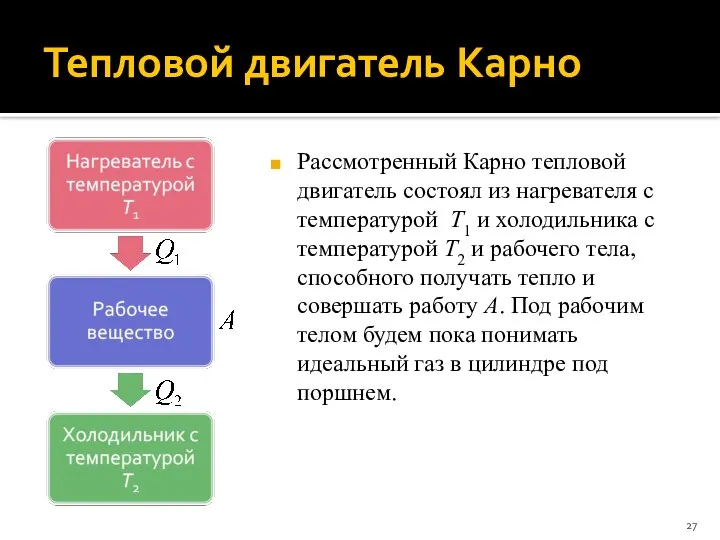
- 27. Тепловой двигатель Карно Рассмотренный Карно тепловой двигатель состоял из нагревателя с температурой T1 и холодильника с
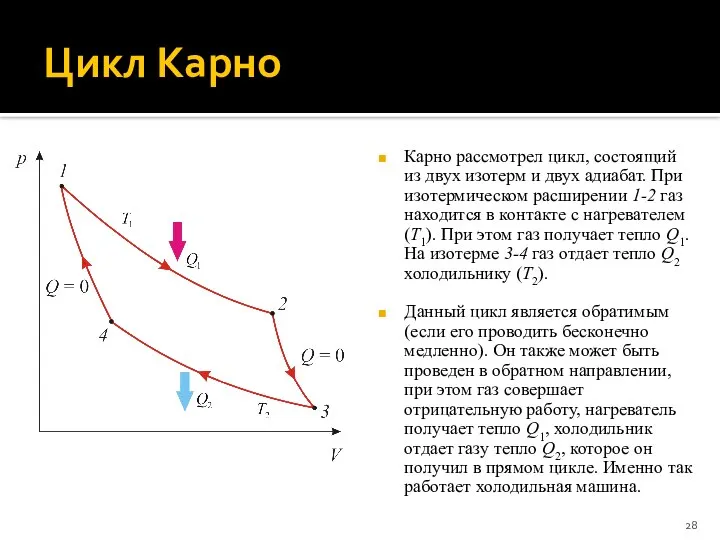
- 28. Цикл Карно Карно рассмотрел цикл, состоящий из двух изотерм и двух адиабат. При изотермическом расширении 1-2
- 29. Вывод формулы для КПД цикла Карно На диаграмме TS цикл Карно имеет вид прямоугольника с изотермами
- 30. КПД цикла Карно Тогда КПД цикла Карно: При выводе этой формулы не делалось никаких выводов о
- 31. 2-я теорема Карно КПД любого необратимого теплового двигателя, работающего с теми же температурами нагревателя и холодильника,
- 32. Другие процессы на диаграмме TS Решение вопроса о КПД других циклов часто сильно упрощается, если его
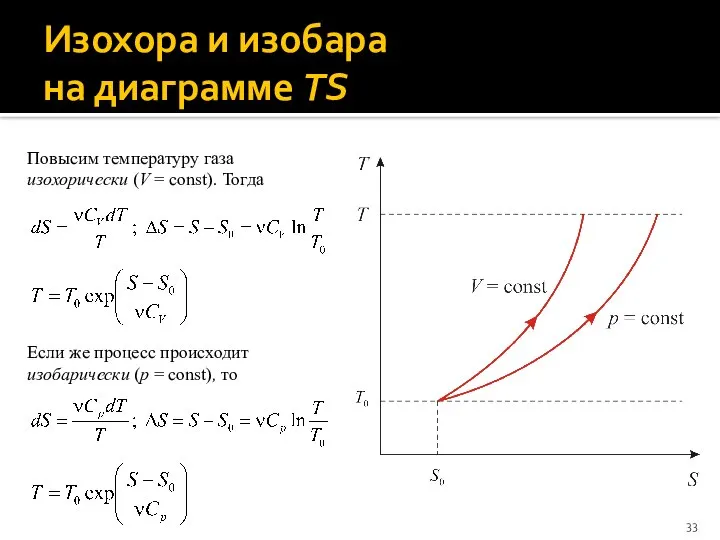
- 33. Изохора и изобара на диаграмме TS Повысим температуру газа изохорически (V = const). Тогда Если же
- 34. 4.5 Энтропия и вероятность. Статистический смысл энтропии ЛЕКЦИЯ 4. ВТОРОЕ И ТРЕТЬЕ НАЧАЛА ТЕРМОДИНАМИКИ
- 35. Макро- и микросостояния системы. Статистический вес Состояние макросистемы, охарактеризованное заданием таких макропараметром, как объем, температура, давление
- 36. Размещение N молекул по двум половинкам сосуда Вероятность одновременного пребывания N молекул в одной и половинок
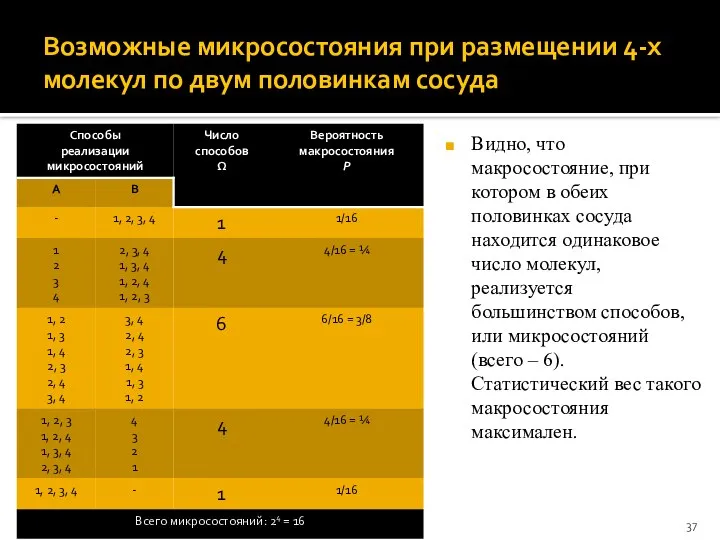
- 37. Возможные микросостояния при размещении 4-х молекул по двум половинкам сосуда Видно, что макросостояние, при котором в
- 38. Самопроизвольное сжатие газа Пусть первоначально все 4 молекул идеального газа находились в половине A. Вследствие беспорядочного
- 39. Случай распределения большого числа молекул по двум половинам сосуда В случае N = 10 получим P
- 40. Вывод Макросистема, будучи предоставленной самой себе, стремится самопроизвольно переходить от менее вероятных макросостояний, к более вероятным.
- 41. Энтропия и вероятность. Формула Больцмана Если макросистема находится в неравновесном состоянии, то она будет самопроизвольно переходить
- 43. Скачать презентацию


































 Чебоксары, Муниципальное образовательное учреждение «Школа № 7» Нет меж живущих людей, да не может и быть безымянных, В первый же миг по рождении каждый, убогий и знатный, И
Чебоксары, Муниципальное образовательное учреждение «Школа № 7» Нет меж живущих людей, да не может и быть безымянных, В первый же миг по рождении каждый, убогий и знатный, И ВКР: «Межкультурная коммуникация как инструмент деловой и корпоративной культуры»
ВКР: «Межкультурная коммуникация как инструмент деловой и корпоративной культуры» Усиление деревянных конструкций (1)
Усиление деревянных конструкций (1) Воспаление
Воспаление  Відкриваюча промова – практичні поради для адвокатів
Відкриваюча промова – практичні поради для адвокатів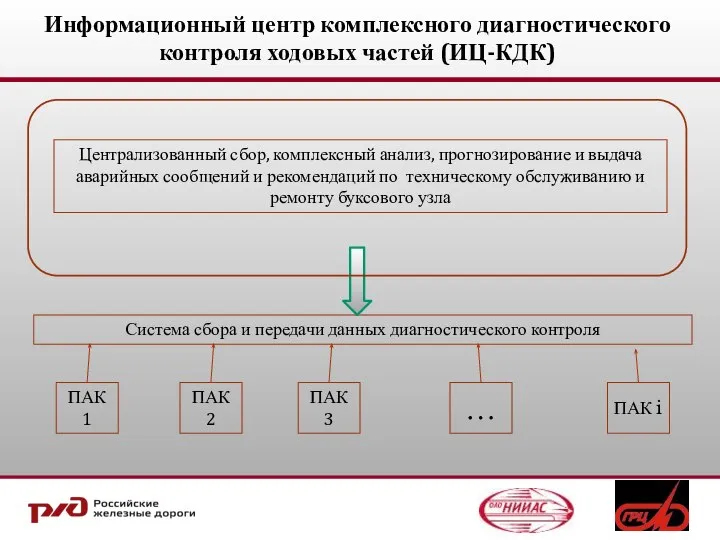 Информационный центр комплексного диагностического контроля ходовых частей (ИЦ-КДК)
Информационный центр комплексного диагностического контроля ходовых частей (ИЦ-КДК) Памятник "Лемболовская твердыня” перешел в собственность Ленинградской области
Памятник "Лемболовская твердыня” перешел в собственность Ленинградской области Валы и оси редуктора
Валы и оси редуктора Костюмированные шоу, как средство формирования культуры праздника
Костюмированные шоу, как средство формирования культуры праздника Подарки детям я несу… (кое-что о дедах морозах мира)
Подарки детям я несу… (кое-что о дедах морозах мира) Солнцевская организованная преступная группировка Выполнили: Трушко П.О. и Тимченко Н.Н.
Солнцевская организованная преступная группировка Выполнили: Трушко П.О. и Тимченко Н.Н.  Алгоритмы и исполнители
Алгоритмы и исполнители Презентация по истории культуры России Великий Новгород Кремль и Ярославово дворище
Презентация по истории культуры России Великий Новгород Кремль и Ярославово дворище Школа 2000 (Новицкая А.Н.)
Школа 2000 (Новицкая А.Н.) The christmas quiz
The christmas quiz Проектная подготовка в строительстве
Проектная подготовка в строительстве Компьютердің конструктивті құрылғылары
Компьютердің конструктивті құрылғылары Выполнила: студент 3 курса (303 группа) факультета ВСО форма обучения: заочная Швачко.А.В.
Выполнила: студент 3 курса (303 группа) факультета ВСО форма обучения: заочная Швачко.А.В. Ультразвуковой контроль
Ультразвуковой контроль Задачи педагогического коллектива по повышению эффективности здоровьесбережения школьников и безопасных условий обучения
Задачи педагогического коллектива по повышению эффективности здоровьесбережения школьников и безопасных условий обучения Многозональные вытяжные вентиляторы
Многозональные вытяжные вентиляторы Организация финансового контроля проведения торгов в сфере гос. и мун. закупок
Организация финансового контроля проведения торгов в сфере гос. и мун. закупок  Лапшина Ольга Ивановна Учитель английского языка. МОУ Первомайская СОШ
Лапшина Ольга Ивановна Учитель английского языка. МОУ Первомайская СОШ МАОУ «Школа № 176». Команда Зарничников
МАОУ «Школа № 176». Команда Зарничников Безопасность предпринимательской деятельности
Безопасность предпринимательской деятельности Механическая коробка передач
Механическая коробка передач Семь русских чайных традиций
Семь русских чайных традиций Модели торговли и логистики
Модели торговли и логистики