Содержание
- 2. Берман Г.Н. Сборник задач по курсу математического анализа: учеб пособие. СПб.: Лань, 2007. – 448 с.
- 3. §1. Введение в анализ (основные понятия) §2. Числовые множества §3. Функции Содержание лекции
- 4. В математике для сокращения записей используются некоторые простейшие логические символы: α ⇒ β − «из предложения
- 5. §2. Числовые множества
- 6. §2. Числовые множества (продолжение)
- 7. §2. Числовые множества (продолжение)
- 8. §2. Числовые множества (продолжение)
- 9. Пусть a и b − действительные числа, причем a Df: Числовыми промежутками на числовой оси называют
- 10. Df: Числа a и b называются, соответственно, левым и правым концами этих промежутков. Символы −∞ и
- 11. Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением зависимости (связи, соответствия)
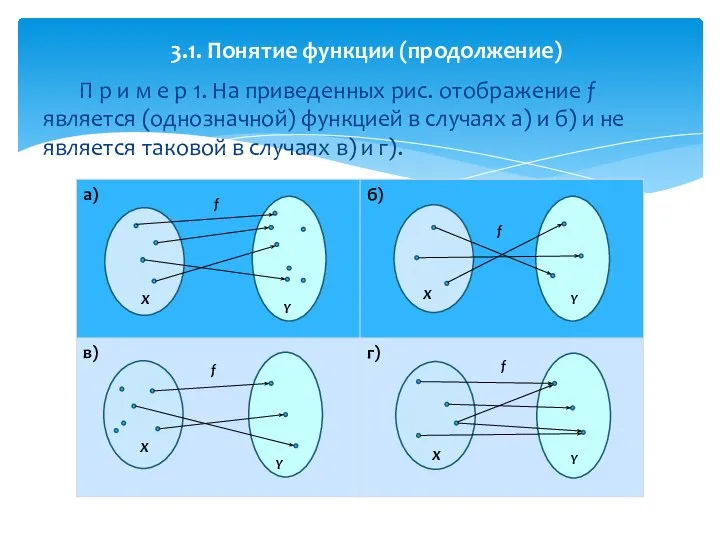
- 12. П р и м е р 1. На приведенных рис. отображение f является (однозначной) функцией в
- 13. Пусть задана функция f: X → Y. Df: Если элементами множеств X и Y являются действительные
- 14. Df: Графиком функции y = f(x) называется множество всех точек плоскости Oxy, для каждой из которых
- 15. 3.2. Числовые функции (продолжение)
- 16. 3.2. Числовые функции (продолжение)
- 17. 3.2. Числовые функции (продолжение)
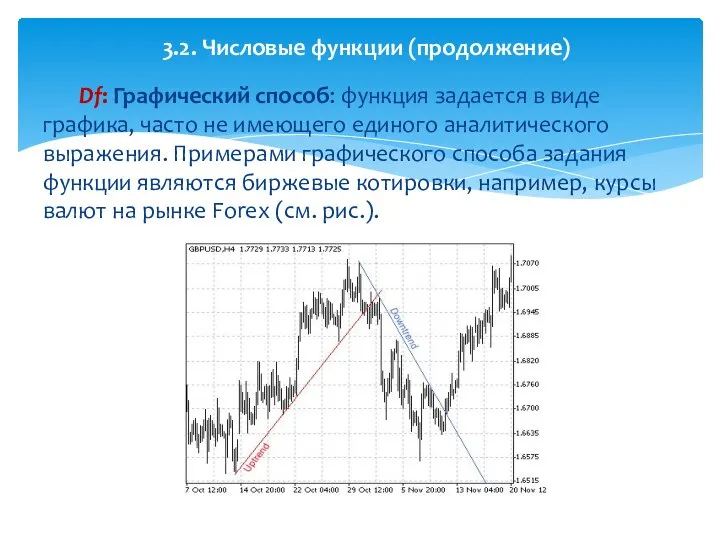
- 18. Df: Графический способ: функция задается в виде графика, часто не имеющего единого аналитического выражения. Примерами графического
- 19. Нередко графики вычерчиваются автоматически самопишущими приборами или изображаются на экране дисплея. Значения функции y, соответствующие тем
- 20. 3.3. Основные характеристики функций
- 21. Пусть функция y = f(x) определена на множестве D и пусть область D1 ⊂ D. Df:
- 22. 3.3. Основные характеристики функций (продолжение)
- 23. Df: Функция y = f(x), определенная на множестве D, называются периодической на этом множестве, если существует
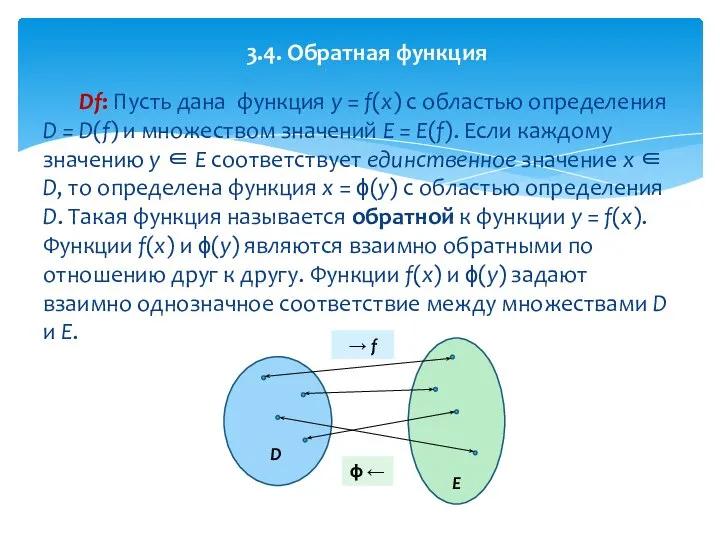
- 24. Df: Пусть дана функция y = f(x) с областью определения D = D(f) и множеством значений
- 25. 3.4. Обратная функция (продолжение)
- 26. Сказанное означает, что точка M1(x0; y0) кривой прямой функции y = f(x) становится точкой M2(y0; x0)
- 27. Df: Пусть функция y = f(u) определена на множестве D = D(f), а функция u =
- 28. Основными элементарными функциями называют нижеследующие функции y = f(x). 1. Степенная функция y = xα, α
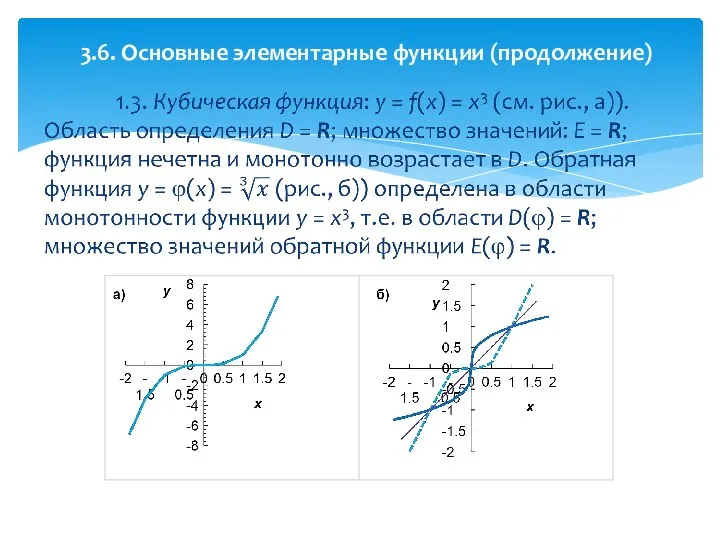
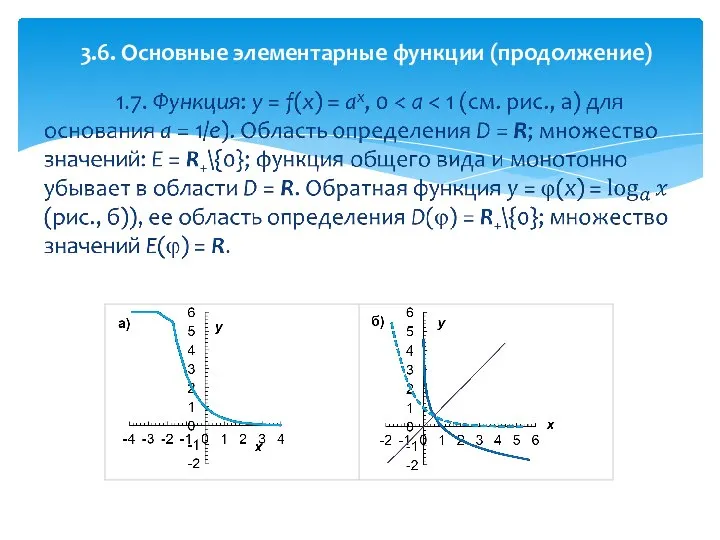
- 29. 3.6. Основные элементарные функции (продолжение)
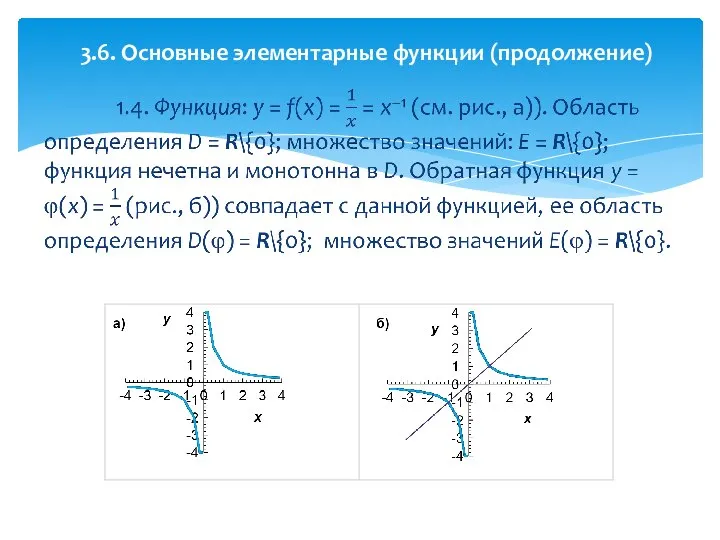
- 30. 3.6. Основные элементарные функции (продолжение)
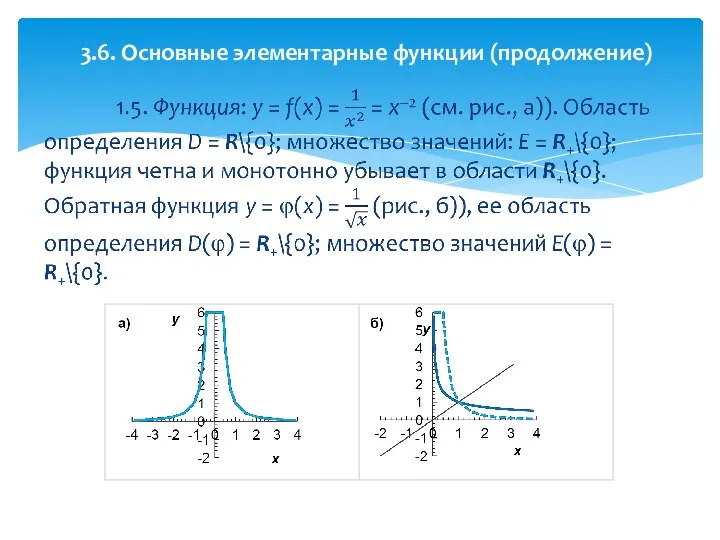
- 31. 3.6. Основные элементарные функции (продолжение)
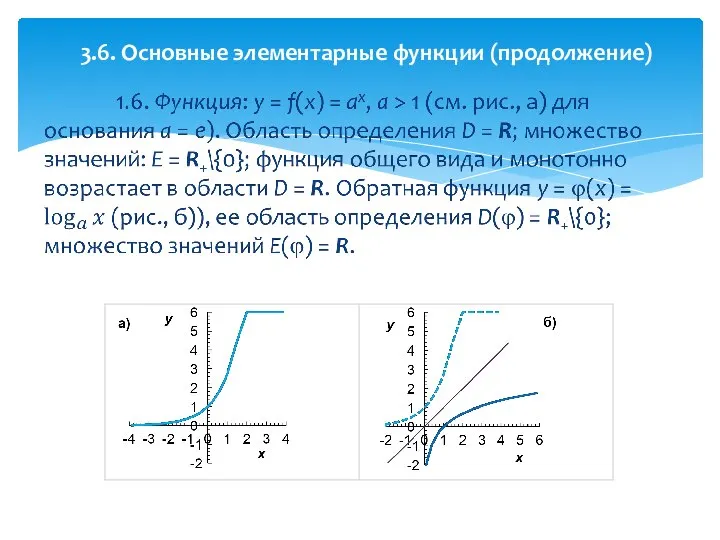
- 32. 3.6. Основные элементарные функции (продолжение)
- 33. 3.6. Основные элементарные функции (продолжение)
- 34. 3.6. Основные элементарные функции (продолжение)
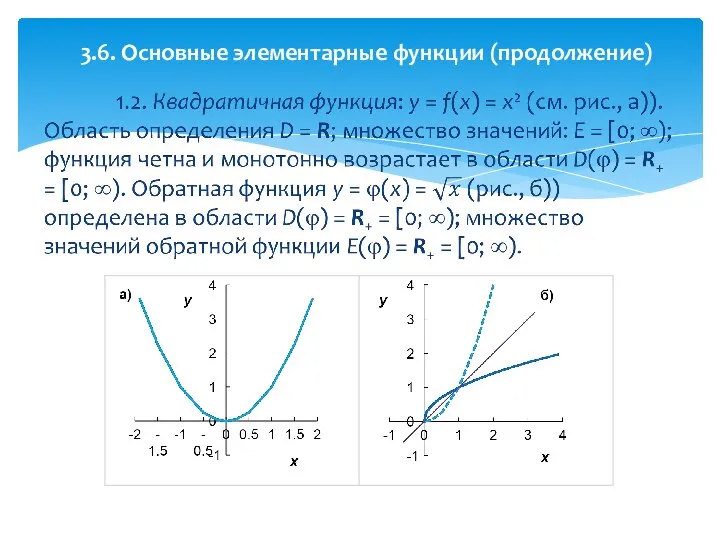
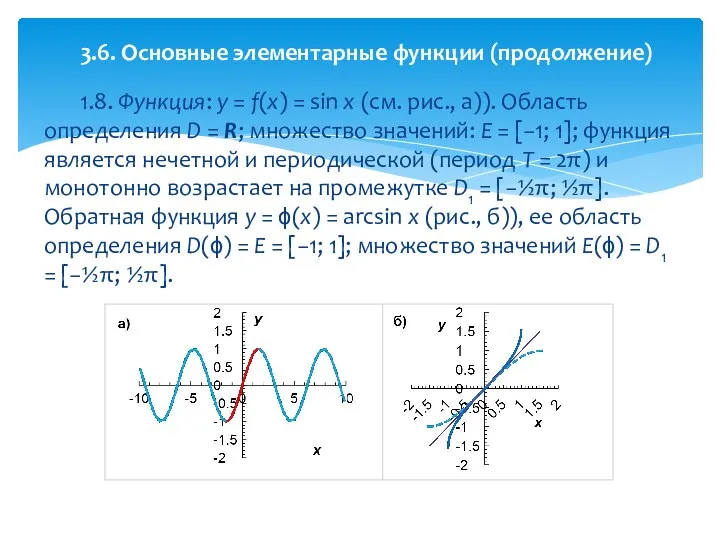
- 35. 1.8. Функция: y = f(x) = sin x (см. рис., а)). Область определения D = R;
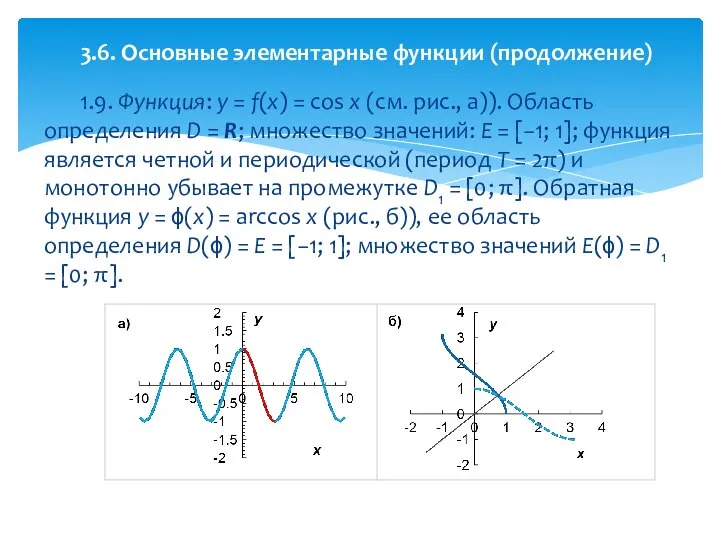
- 36. 1.9. Функция: y = f(x) = cos x (см. рис., а)). Область определения D = R;
- 37. 1.10. Функция: y = f(x) = tg x (см. рис., а)). Область определения D = R\{π(n
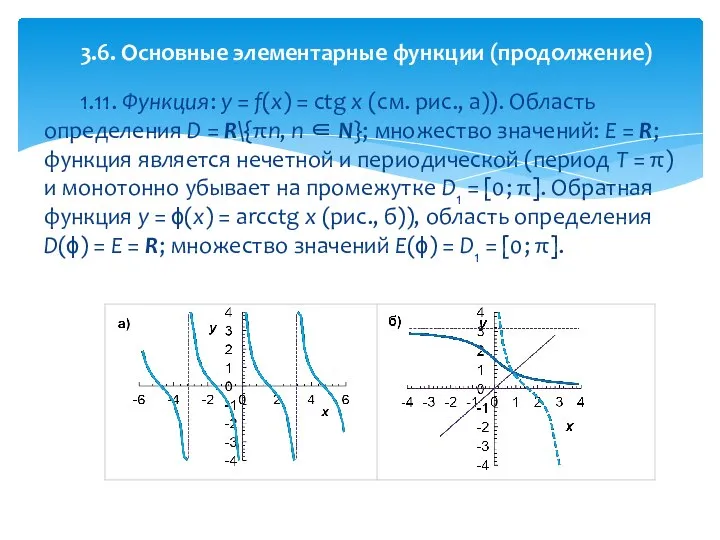
- 38. 1.11. Функция: y = f(x) = ctg x (см. рис., а)). Область определения D = R\{πn,
- 39. 3.5. Сложная функция
- 41. Скачать презентацию


























 Тест по устройству ЯЛ-6
Тест по устройству ЯЛ-6 Электоральный юрист
Электоральный юрист Новый год в Италии
Новый год в Италии JavaScript
JavaScript  Конфликтные и кризисные ситуации в политике
Конфликтные и кризисные ситуации в политике Технология лечебно-косметических мазей
Технология лечебно-косметических мазей Презентация Гражданская война 1919-1920гг.
Презентация Гражданская война 1919-1920гг. Введение в искусственный интеллект
Введение в искусственный интеллект Своеобразие художественной культуры древнейших цивилизаций www.themegallery.com
Своеобразие художественной культуры древнейших цивилизаций www.themegallery.com Правовой статус личности. Тема 1.7
Правовой статус личности. Тема 1.7 Приключения кота Васяна
Приключения кота Васяна Азербайджанские народные игры
Азербайджанские народные игры Каменный век – детство человечества
Каменный век – детство человечества Задачи по инженерной графике
Задачи по инженерной графике Информационно-коммуникационные технологии и их роль в жизни общества
Информационно-коммуникационные технологии и их роль в жизни общества Деньги… цель или средство? Проблемный диалог Классный час в 10 классе Классный руководитель Захарова О.В. МОУ «СОШ с.Воскресенское»
Деньги… цель или средство? Проблемный диалог Классный час в 10 классе Классный руководитель Захарова О.В. МОУ «СОШ с.Воскресенское»  Презентация "Три ступени – Три Дохода" - скачать презентации по Экономике
Презентация "Три ступени – Три Дохода" - скачать презентации по Экономике Курсы по тестированию IT LABS. Баг. (Урок 3)
Курсы по тестированию IT LABS. Баг. (Урок 3) Шет ел азаматтары мен азаматтығы жоқ тұлғалар бойынша азаматтық іс жүргізу
Шет ел азаматтары мен азаматтығы жоқ тұлғалар бойынша азаматтық іс жүргізу Взаимное положение прямой и плоскости
Взаимное положение прямой и плоскости  Изменяющийся контекст и вызовы, стоящие перед системой образования В.А.Болотов
Изменяющийся контекст и вызовы, стоящие перед системой образования В.А.Болотов Тем.3.Зан.2.мод.ppt
Тем.3.Зан.2.мод.ppt Обсуждаемые вопросы городского совещания педагогов – кураторов ЗОЖ : 1. Задачи и основные направления деятельности ОО муниципа
Обсуждаемые вопросы городского совещания педагогов – кураторов ЗОЖ : 1. Задачи и основные направления деятельности ОО муниципа Давайте познакомимся!
Давайте познакомимся! Смешанные единоборства
Смешанные единоборства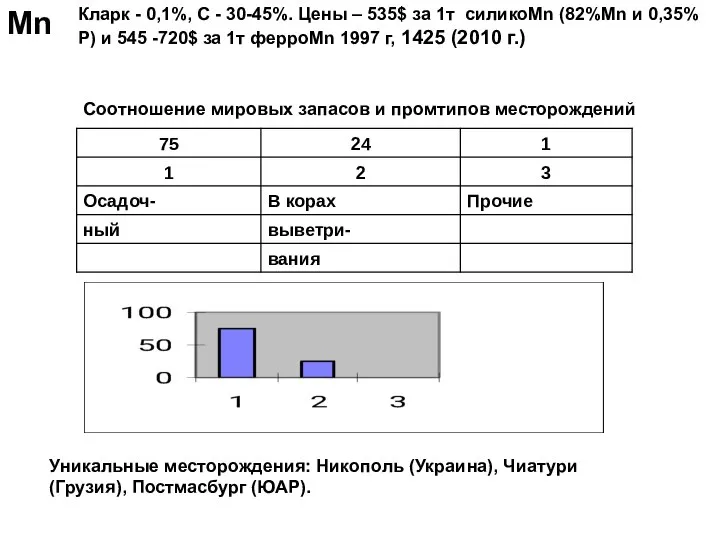 Марганцевые руды
Марганцевые руды  Презентация на тему "Психологическая характеристика гиперактивных детей" - скачать презентации по Медицине
Презентация на тему "Психологическая характеристика гиперактивных детей" - скачать презентации по Медицине Последствия глобализации и профсоюзы (The Impact of Globalisation and Trade Unions) Основные проблемы для рабочего движения (Main Challenges for the Labour Movemen
Последствия глобализации и профсоюзы (The Impact of Globalisation and Trade Unions) Основные проблемы для рабочего движения (Main Challenges for the Labour Movemen