Содержание
- 2. Берман Г.Н. Сборник задач по курсу математического анализа: учеб пособие. СПб.: Лань, 2007. – 448 с.
- 3. §1. Основные понятия §2. Решение систем линейных уравнений. Теорема Кронекера - Капелли §3. Решение невырожденных линейных
- 4. Цель занятия: развитие средствами изучаемой дисциплины общекультурных и профессиональных компетенций, регламентируемых ФГОС ВПО направлению «080400 –
- 5. §1. Основные понятия
- 6. §1. Основные понятия (продолжение)
- 7. §1. Основные понятия (продолжение)
- 8. Df: Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она
- 9. §1. Основные понятия (продолжение)
- 10. §2. Решение систем линейных уравнений. Теорема Кронекера - Капелли
- 11. Правила практического разыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем. Т е о
- 12. 2. Если r(A) = r(Ā) = r, система совместна. Найти какой-либо базисный минор порядка r. Взять
- 13. §2. Решение систем линейных уравнений. Теорема Кронекера – Капелли (продолжение)
- 14. §2. Решение систем линейных уравнений. Теорема Кронекера – Капелли (продолжение)
- 15. §2. Решение систем линейных уравнений. Теорема Кронекера – Капелли (продолжение)
- 16. §3. Решение невырожденных линейных систем. Формулы Крамера
- 17. Заметим, что если detA ≠ 0, то ранг матрицы системы линейных уравнений r(A) = n =
- 18. §3. …Формулы Крамера (продолжение)
- 19. §3. …Формулы Крамера (продолжение)
- 20. §3. …Формулы Крамера (продолжение)
- 21. §3. …Формулы Крамера (продолжение)
- 22. §3. …Формулы Крамера (продолжение)
- 23. §4. Решение систем линейных уравнений методом Гаусса
- 24. §4. Решение систем линейных уравнений методом Гаусса (продолжение)
- 25. §4. …метод Гаусса (продолжение)
- 26. §4. …метод Гаусса (продолжение)
- 27. О б р а т н ы й х о д. Второй этап (обратный ход) заключается
- 28. З а м е ч а н и е 1. Если ступенчатая система оказывается треугольной, т.е.
- 29. §4. …метод Гаусса (продолжение)
- 30. §4. …метод Гаусса (продолжение)
- 31. §5. Системы линейных однородных уравнений
- 32. §5. Системы линейных однородных уравнений (продолжение)
- 33. Т е о р е м а. Для того, чтобы однородная система n линейных уравнений с
- 34. §5. Системы однородных уравнений (продолжение)
- 36. Скачать презентацию

































 Отчет о прохождении производственной практики (по профилю специальности)
Отчет о прохождении производственной практики (по профилю специальности) Презентация Таможенный тариф 1724 года. Принятие морского пошлинного тарифа 1731. Выполнила: Жукова Юлия Т-1203
Презентация Таможенный тариф 1724 года. Принятие морского пошлинного тарифа 1731. Выполнила: Жукова Юлия Т-1203 Религия. Структура религии
Религия. Структура религии Глава 21. Консультирование по вопросам всеобщего управления качеством
Глава 21. Консультирование по вопросам всеобщего управления качеством Les symboles du l'Ukraine
Les symboles du l'Ukraine Аплети
Аплети  Презентация Социологическая теория права:общая характеристика
Презентация Социологическая теория права:общая характеристика  Паркур – искусство рационального передвижения по городу
Паркур – искусство рационального передвижения по городу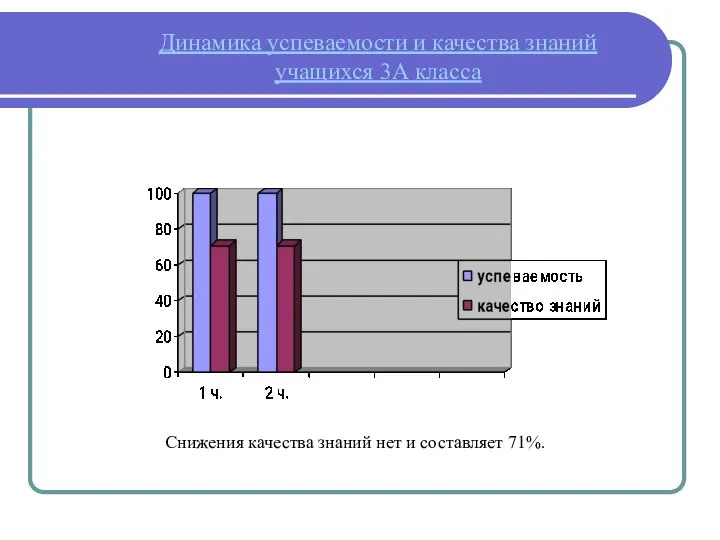 Динамика успеваемости и качества знаний учащихся 3А класса
Динамика успеваемости и качества знаний учащихся 3А класса Локальные сети
Локальные сети Проект «Донская жемчужина»
Проект «Донская жемчужина» ИПО_Раздел 1
ИПО_Раздел 1 Main trends of international cooperation in combating сrimes
Main trends of international cooperation in combating сrimes Carnival of Venice. Carnival in Rio de Janeiro
Carnival of Venice. Carnival in Rio de Janeiro System polityczny w stanach zjednoczone
System polityczny w stanach zjednoczone Иннокентий Фёдорович Анненский (1856 – 1909)
Иннокентий Фёдорович Анненский (1856 – 1909) Устройство и принцип действия асинхронного двигателя
Устройство и принцип действия асинхронного двигателя Театральное искусство XVII – XVIII вв.
Театральное искусство XVII – XVIII вв.  Налоги, банки, бизнес 2019
Налоги, банки, бизнес 2019 Площади фигур 5 класс
Площади фигур 5 класс ВК. Великая российская революция. Октябрь 1917 г.
ВК. Великая российская революция. Октябрь 1917 г. Хронические неспецифические заболевания лёгких у детей Хронические неспецифические заболевания лёгких у детей
Хронические неспецифические заболевания лёгких у детей Хронические неспецифические заболевания лёгких у детей Как живописцы изображают пространство Выполнил ученик 10 класса: Осфальд Алексей
Как живописцы изображают пространство Выполнил ученик 10 класса: Осфальд Алексей Информационные технологии
Информационные технологии Государство
Государство Основные положения Федерального Закона об основах туристкой деятельности» в РФ
Основные положения Федерального Закона об основах туристкой деятельности» в РФ ПОНЯТИЕ «МЕТОДА», «МЕТОДИКИ» И «МЕТОДОЛОГИИ» НАУЧНОГО ПОЗНАНИЯ. ИХ ВЗАИМОСВЯЗЬ. Подготовила студентка 1 курса ФТД группы Т-1207 Пон
ПОНЯТИЕ «МЕТОДА», «МЕТОДИКИ» И «МЕТОДОЛОГИИ» НАУЧНОГО ПОЗНАНИЯ. ИХ ВЗАИМОСВЯЗЬ. Подготовила студентка 1 курса ФТД группы Т-1207 Пон Степень и её свойства - презентация по Алгебре
Степень и её свойства - презентация по Алгебре