Содержание
- 2. Лекция 6 0. Задача о большинстве Об индивидуальных заданиях О возможностях метода Хоара (Соотношение между хоаровскими
- 3. Об индивидуальных заданиях … 21.04.2015 О возможностях метода Хоара 1
- 4. О возможностях метода Хоара Абрамов С.А. Элементы анализа программ. Частичные функции на множестве состояний. – М.:
- 5. Преамбула 21.04.2015 О возможностях метода Хоара 1
- 6. 21.04.2015 Аннотирование цикла и понимание аннотаций Цикл рекомендуется оформлять следующим образом: //@ Pred Q: предусловие //@
- 7. 21.04.2015 Список условий для проверки (аннотированного) цикла 1) показать, что P – истинно до выполнения цикла,
- 8. 21.04.2015 Пример: int i, n; //@ n > 0 i = 1; //@ inv P: (0
- 9. 21.04.2015 3) Утверждение !B есть (2*i > n). Отсюда очевидно, что (!B & inv) ≡ post
- 10. О переменных-призраках int i, n; //@ n > 0 i = 1; // int j =
- 11. Альтернатива – использование кванторов int i, n; //@ n > 0 i = 1; //@ inv
- 13. Скачать презентацию










 Православные праздники
Православные праздники учитель начальных классов ГОУ (гимназия) №498
учитель начальных классов ГОУ (гимназия) №498 «…современный урок должен стать уроком творческой дружбы учителя и ученика.» (Куманев А.А.). Примерная структура каждого типа урока по ФГОС
«…современный урок должен стать уроком творческой дружбы учителя и ученика.» (Куманев А.А.). Примерная структура каждого типа урока по ФГОС Джон Стюарт Милль Подготовила: студентка Группы Ю092 Виноградская Екатерина
Джон Стюарт Милль Подготовила: студентка Группы Ю092 Виноградская Екатерина Международное сотрудничество в области экологии
Международное сотрудничество в области экологии ПРЕПАРАТЫ СТЕРОИДНЫХ ГОРМОНОВ, ИХ СИНТЕТИЧЕСКИХ ЗАМЕНИТЕЛЕЙ И АНТАГОНИСТОВ
ПРЕПАРАТЫ СТЕРОИДНЫХ ГОРМОНОВ, ИХ СИНТЕТИЧЕСКИХ ЗАМЕНИТЕЛЕЙ И АНТАГОНИСТОВ Гр. заняття Т-3.3.ВА.ppt
Гр. заняття Т-3.3.ВА.ppt Міст. Патерни проектування
Міст. Патерни проектування Инвалидность и реабилитация как медико-социальная проблема
Инвалидность и реабилитация как медико-социальная проблема Jakob und Wilhel Grimm
Jakob und Wilhel Grimm Тіл мәдениет
Тіл мәдениет Классификация тары и упаковочных материалов
Классификация тары и упаковочных материалов 7Оценка эффективности здравоохранения.ppt
7Оценка эффективности здравоохранения.ppt Футбол. История футбола
Футбол. История футбола Презентация 2.1.2_Дыхание
Презентация 2.1.2_Дыхание Конституция РФ - основной закон государства
Конституция РФ - основной закон государства Виды принтеров. Плюсы и минусы
Виды принтеров. Плюсы и минусы Богоматерь Владимирская. Первая треть XII в
Богоматерь Владимирская. Первая треть XII в Буришин Олеся Анатоліївна - презентация для начальной школы
Буришин Олеся Анатоліївна - презентация для начальной школы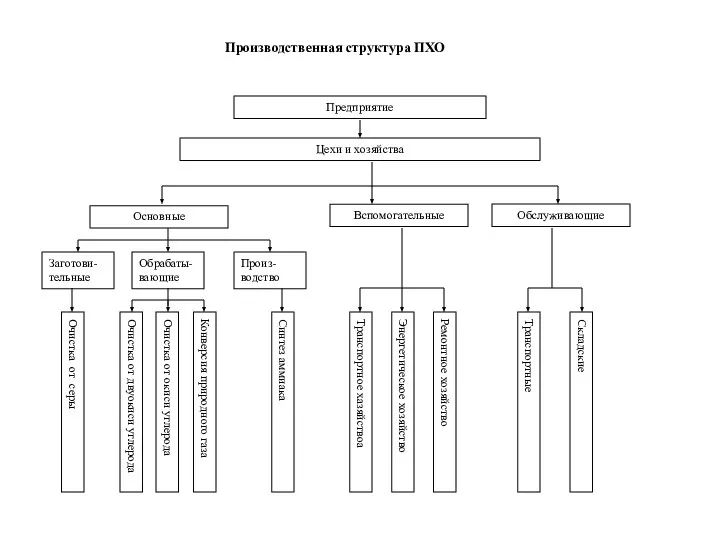 Производственная структура ПХО
Производственная структура ПХО Основные показатели безотказности
Основные показатели безотказности Выполнила: ученица 8 «В» Ермакова Лиза
Выполнила: ученица 8 «В» Ермакова Лиза  Телетайп - электромеханическая печатная машина,
Телетайп - электромеханическая печатная машина, «Исторические этапы в развитии логики» Работу выполнили студентки 2курса уч.группы ТС 01/1301 Доценко Юлия и Опутина Анна
«Исторические этапы в развитии логики» Работу выполнили студентки 2курса уч.группы ТС 01/1301 Доценко Юлия и Опутина Анна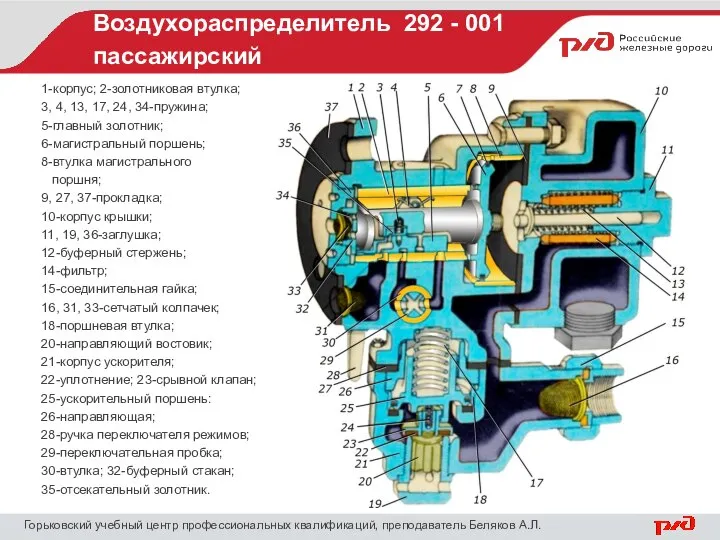 Воздухораспределитель 292 - 001 пассажирский
Воздухораспределитель 292 - 001 пассажирский Презентация Таможенная ревизия
Презентация Таможенная ревизия Бразильский карнавал
Бразильский карнавал Москва 7 декабря 2010 года
Москва 7 декабря 2010 года