Содержание
- 2. Пример к Лекции 5 Задача о большинстве массива 14.04.2015 О схемах программ
- 3. Пример: массив с большинством Определение: массив x1, x2, …, xn содержит большинство, если более половины его
- 4. Пояснения Элемент a в массиве Х [1 .. п] является элементом большинства ттогда, когда a появляется
- 5. Решения Простой алгоритм: для каждого элемента подсчитывать число вхождений, пока не встретится элемент, образующий большинство. Сложность
- 6. Вариант рандомизированного алгоритма Случайно выбираем i (равновероятно), а затем проверяем, удовлетворяет ли xi условию большинства. do
- 7. Сложность рандомизированного алгоритма Фиксируем размер входа n. Множество всех возможных сценариев – множество кортежей (i1, i2,
- 8. Рекуррентное уравнение Средние затраты t=t(n) есть t = P*n + (1-P)*(t + n), где P -
- 9. «Дерандомизация» Идея: За основу берется рандомизированный алгоритм и случайный выбор заменяется на нерандомизированный (детерминированный) Выбор кандидата
- 10. Наблюдения (наводящие соображения) Если два различных элемента удаляются из массива X, то большинство старого массива остается
- 11. Algorithm: Majority Вход: x[1..n] Выход: Элемент большинства, если большинство существует, иначе ответ «нет». ------------------------------------------------------------------- c =
- 12. Функция Candidate(m) { j = m; c =x[m]; count = 1; While ( (j 0)) {
- 13. Не рекурсивная функция Candid1 { count = 1; c = x[1]; for (j = 2; j
- 14. Не рекурсивная функция Candid2 { count = 0; // c = x[1]; for (j = 1;
- 15. int Majority(int X[], int n) {// C++, т.е. X[0..n-1] int Candidate; int i = 0; int
- 16. Примеры x[1..13] = 3131313131313 Count > 0, и имеется большинство x[13]=3 x[1..9] = 123456777 Count >
- 17. Продолжение x[1..9] = 555551234 55555 {count=5} 555551 {count=4} 5555512 {count=3} 55555123 {count=2} 555551234 {count=1} !!! x[1..9]
- 19. Скачать презентацию


![Пояснения Элемент a в массиве Х [1 .. п] является элементом](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1307761/slide-3.jpg)






![Algorithm: Majority Вход: x[1..n] Выход: Элемент большинства, если большинство существует, иначе](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1307761/slide-10.jpg)
![Функция Candidate(m) { j = m; c =x[m]; count = 1;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1307761/slide-11.jpg)
![Не рекурсивная функция Candid1 { count = 1; c = x[1];](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1307761/slide-12.jpg)

![int Majority(int X[], int n) {// C++, т.е. X[0..n-1] int Candidate;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1307761/slide-14.jpg)
![Примеры x[1..13] = 3131313131313 Count > 0, и имеется большинство x[13]=3](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1307761/slide-15.jpg)
![Продолжение x[1..9] = 555551234 55555 {count=5} 555551 {count=4} 5555512 {count=3} 55555123](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1307761/slide-16.jpg)
 Квалификационный экзамен ПМ 04
Квалификационный экзамен ПМ 04 «Синдром профессионального выгорания»
«Синдром профессионального выгорания» Виталий Валентинович Бианки
Виталий Валентинович Бианки ОКС_2019
ОКС_2019 Здоровий спосіб життя. Харчування і фізична культура
Здоровий спосіб життя. Харчування і фізична культура Нетрадиционные системы физических упражнений
Нетрадиционные системы физических упражнений Презентация Налогообложение физических лиц
Презентация Налогообложение физических лиц Возможности развития одаренных детей Проект программы развития «Одаренные дети» на 2008 -2011 учебный год
Возможности развития одаренных детей Проект программы развития «Одаренные дети» на 2008 -2011 учебный год Презентация как один из способов предъявления достижений классного коллектива
Презентация как один из способов предъявления достижений классного коллектива О некоторых правилах оформления чертежей и схем
О некоторых правилах оформления чертежей и схем Граничний стан будівельних об'єктів. Лекція №5
Граничний стан будівельних об'єктів. Лекція №5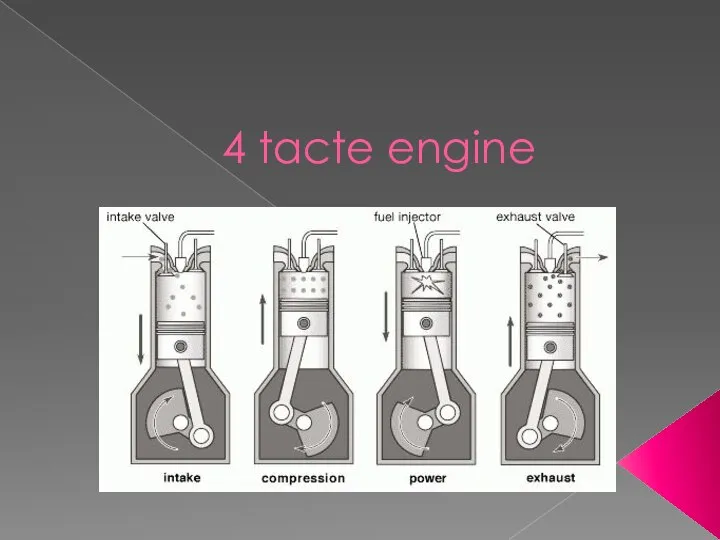 Four strokes of the engine
Four strokes of the engine Litania do Opatrzności Boskiej
Litania do Opatrzności Boskiej Радиобиология 7
Радиобиология 7 Финансовая безопасность России Подготовил: студент ФТД-4 группы Т-093 Воробьев Дм.Ник.
Финансовая безопасность России Подготовил: студент ФТД-4 группы Т-093 Воробьев Дм.Ник. Уникальные секреты цвета и формы
Уникальные секреты цвета и формы Электрические станции и подстанции. Введение. Основные понятия, термины и определения
Электрические станции и подстанции. Введение. Основные понятия, термины и определения Разработка и исследование систем автоматизированного тестирования СОРМ
Разработка и исследование систем автоматизированного тестирования СОРМ Современная тибеткая медицина Подготовили: студентки 218 группы по специальности лечебное дело Воробьёва С.А. Михайлова Ю.А.
Современная тибеткая медицина Подготовили: студентки 218 группы по специальности лечебное дело Воробьёва С.А. Михайлова Ю.А.  Портфоліо 9-А класу
Портфоліо 9-А класу Экономика - презентация для начальной школы
Экономика - презентация для начальной школы Предмет социальной политики и технология социальной работы
Предмет социальной политики и технология социальной работы «Перебудова» та розпад Радянського Союзу
«Перебудова» та розпад Радянського Союзу Генезис и становление теоретического знания в античной культуре
Генезис и становление теоретического знания в античной культуре Законодательные и нормативно-правовые акты, регулирующие проведение ресурсосбережения на объектах коммунального хозяйства
Законодательные и нормативно-правовые акты, регулирующие проведение ресурсосбережения на объектах коммунального хозяйства Материнская плата
Материнская плата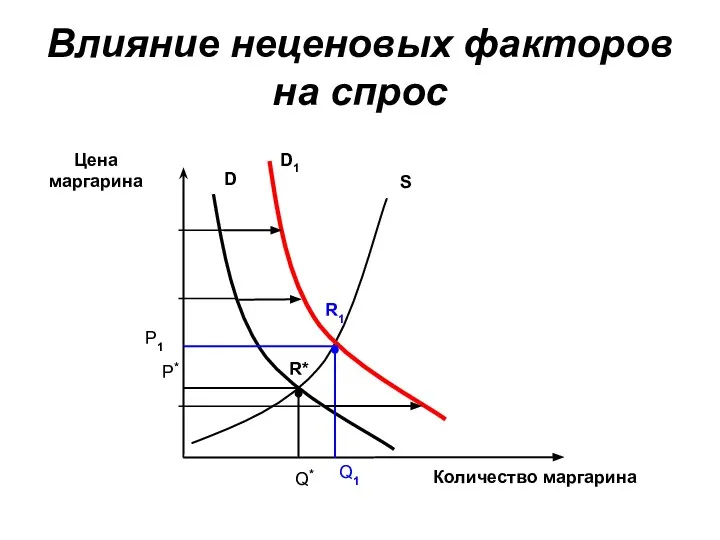 Влияние неценовых факторов на спрос
Влияние неценовых факторов на спрос  Роль религии в современном мире
Роль религии в современном мире