Содержание
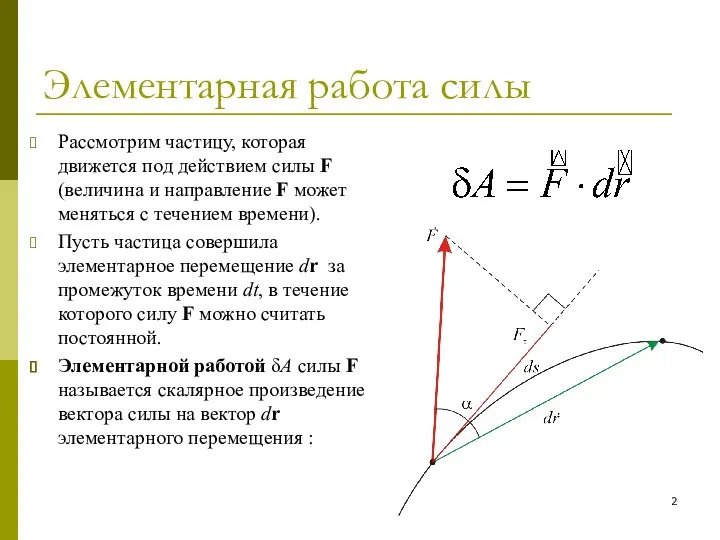
- 2. Элементарная работа силы Рассмотрим частицу, которая движется под действием силы F (величина и направление F может
- 3. Элементарная работа силы Элементарную работу можно представить в другой форме: Здесь α – угол между векторами
- 4. Элементарная работа силы В декартовой прямоугольной системе координат элементарную работу силы F можно представить в виде
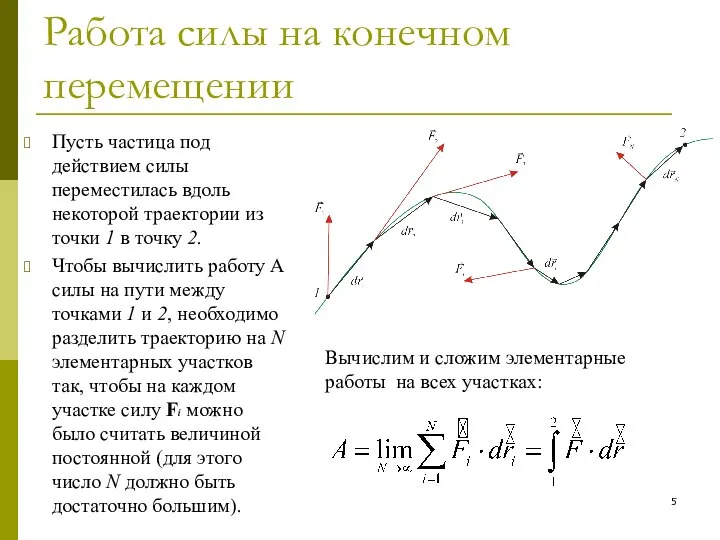
- 5. Работа силы на конечном перемещении Пусть частица под действием силы переместилась вдоль некоторой траектории из точки
- 6. Работа силы на конечном перемещении Таким образом, работа A силы F на конечном пути равна Единицей
- 7. Мощность Мощность – это скалярная физическая величина, которая характеризует работу силы, произведенную в единицу времени. Пусть
- 8. Мощность Мгновенную мощность можно выразить через скорость v движения частицы и действующую на нее силу F:
- 9. Мощность Выразим работу A силы на конечном пути через мгновенную мощность P: С учетом этого соотношения,
- 10. ГЛАВА 4 ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ 4.2 Кинетическая энергия частицы и системы частиц
- 11. Кинетическая энергия частицы Пусть частица массы m движется со скоростью v. Кинетической энергией частицы называется величина:
- 12. Кинетическая энергия системы частиц Кинетическая энергия системы частиц, массы которых m1, m2, …, mi, …, mN,
- 13. Теорема о кинетической энергии частицы Пусть частица массы m движется под действием некоторой силы F (равнодействующая
- 14. Доказательство теоремы о кинетической энергии частицы Работа силы F на элементарном перемещении dr равна: Тогда
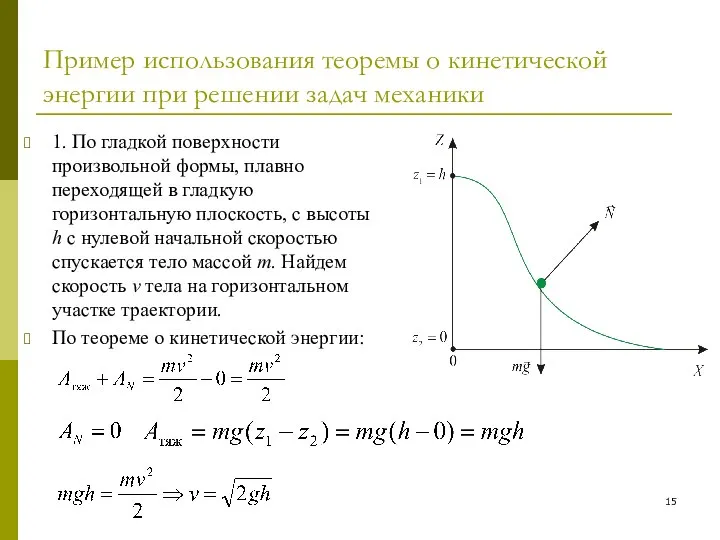
- 15. Пример использования теоремы о кинетической энергии при решении задач механики 1. По гладкой поверхности произвольной формы,
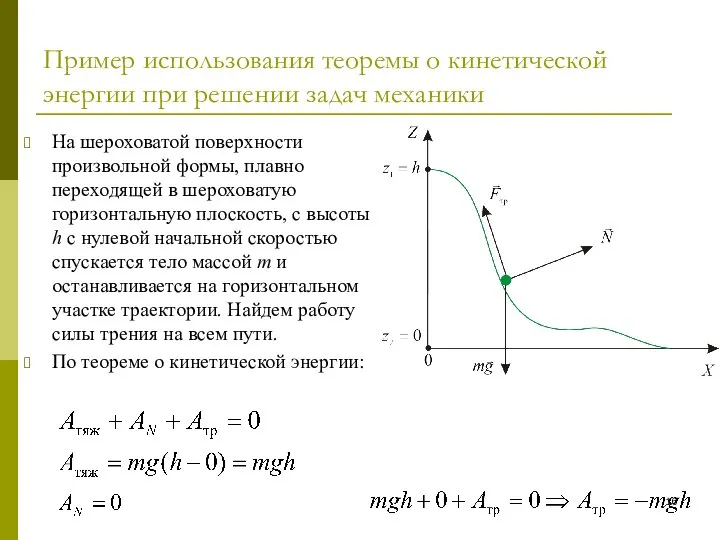
- 16. Пример использования теоремы о кинетической энергии при решении задач механики На шероховатой поверхности произвольной формы, плавно
- 17. ГЛАВА 4 ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ 4.3 Консервативные силы и их свойства
- 18. Силовое поле Если на частицу в каждой точке пространства действует определенная сила, то всю совокупность сил
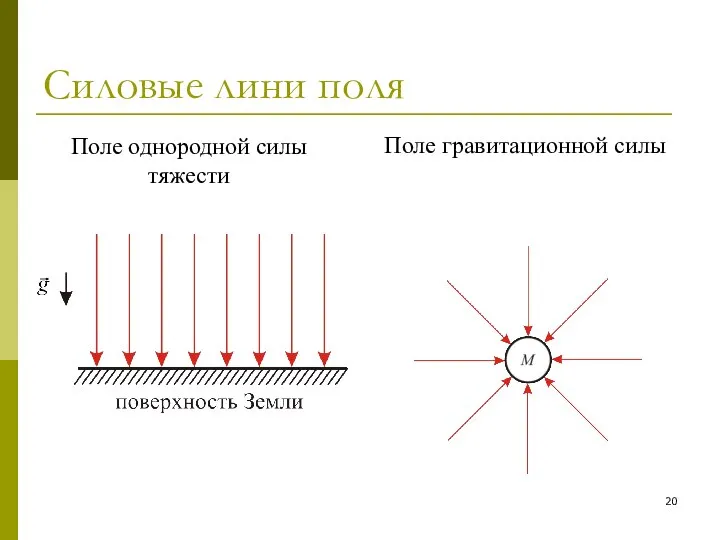
- 19. Силовые линии поля Силовой линией поля называется линия в пространстве, касательная к которой в каждой точке
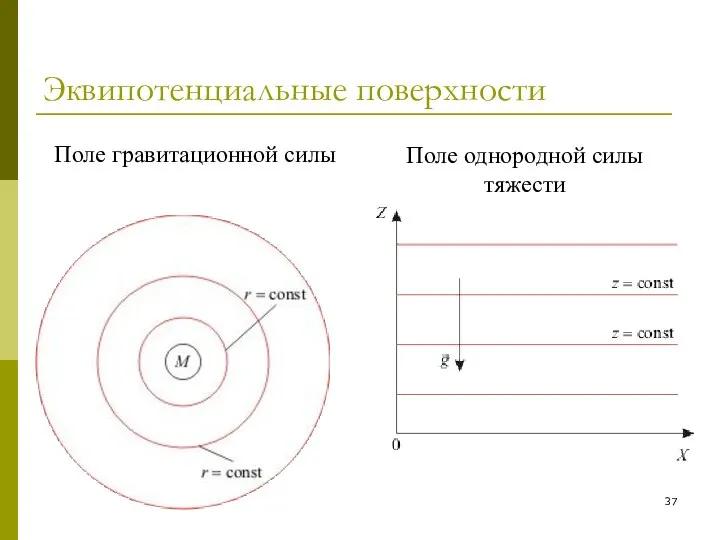
- 20. Силовые лини поля Поле однородной силы тяжести Поле гравитационной силы
- 21. Консервативные силы Консервативным называется поле, в котором совершаемая при перемещении частицы из произвольного начального в произвольное
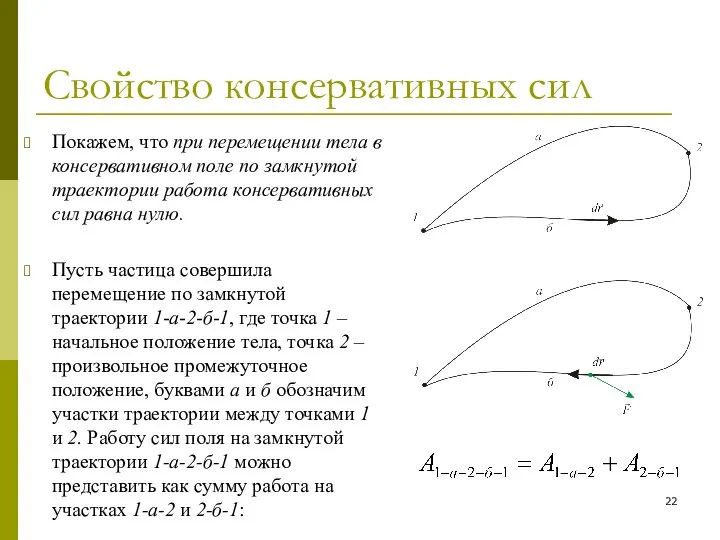
- 22. Свойство консервативных сил Покажем, что при перемещении тела в консервативном поле по замкнутой траектории работа консервативных
- 23. Работа консервативной силы при движении по замкнутой траектории Работа сил поля при перемещении частиц из точки
- 24. ГЛАВА 4 ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ 4.4 Потенциальная энергия частицы и ее свойства
- 25. Потенциальная энергия частицы Рассмотрим консервативное поле. Частица расположена в точке P поля с координатами x, y,
- 26. Свойства потенциальной энергии частицы 1. Потенциальная энергия является функцией только координат x, y, z точки поля,
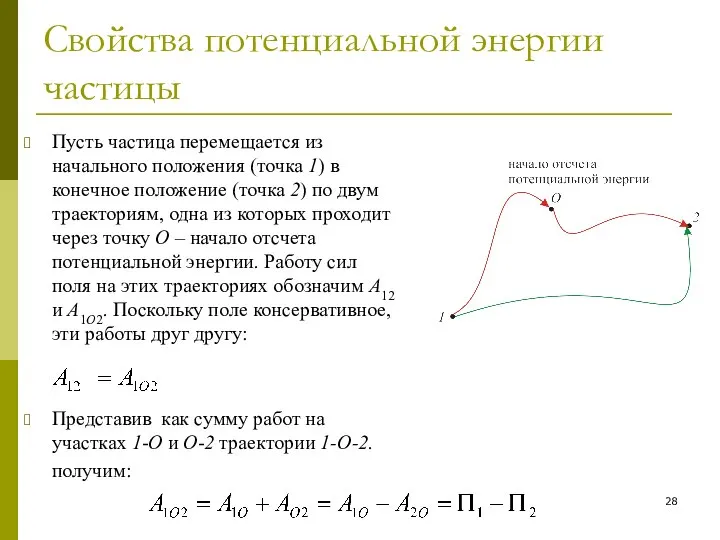
- 27. Свойства потенциальной энергии частицы 2. Работа сил поля при перемещении частицы из произвольного начального в произвольное
- 28. Свойства потенциальной энергии частицы Пусть частица перемещается из начального положения (точка 1) в конечное положение (точка
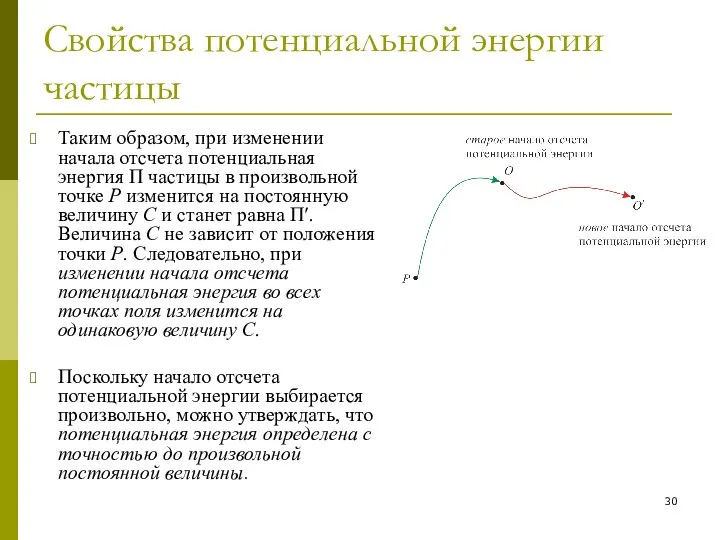
- 29. Свойства потенциальной энергии частицы 3. Потенциальная энергия частицы определена с точностью до произвольной постоянной величины. Поясним
- 30. Свойства потенциальной энергии частицы Таким образом, при изменении начала отсчета потенциальная энергия Π частицы в произвольной
- 31. ГЛАВА 4 ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ 4.5 Связь между силой консервативного поля и потенциальной энергией частицы
- 32. Описание взаимодействия частицы с другими телами Взаимодействие частицы с другими телами можно описывать 2-мя способами: с
- 33. Вывод формулы связи между потенциальной энергией частицы и силой консервативного поля Работа сил консервативного стационарного поля
- 34. Вывод формулы, связи между потенциальной энергией частицы и силой консервативного поля Если аналогично взять частные производные
- 35. Вывод формулы связи между потенциальной энергией частицы и силой консервативного поля Величину, стоящую в скобках, называют
- 36. Формула связи между потенциальной энергией частицы и силой консервативного поля Таким образом, сила F консервативного поля
- 37. Эквипотенциальные поверхности Поле гравитационной силы Поле однородной силы тяжести
- 38. ГЛАВА 4 ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ 4.6 Закон сохранения полной механической энергии частицы
- 39. Полная механическая энергия частицы Пусть частица движется в консервативном силовом поле со скоростью v, а потенциальная
- 40. Закон сохранения полной механической энергии частицы Закон сохранения полной механической энергии частицы. Если на частицу действуют
- 41. Доказательство закона сохранения полной механической энергии частицы Пусть частица переместилась из произвольного положения 1 в произвольное
- 42. Доказательство закона сохранения полной механической энергии частицы Таким образом, Поскольку начальное и конечное положения были выбраны
- 43. Сторонние силы Пусть теперь на частицу при ее движении, помимо консервативных сил, действуют любые другие силы
- 44. Закон изменения полной механической энергии частицы Закон изменения полной механической энергии частицы. Если на частицу помимо
- 46. Скачать презентацию


































 Защита информационных ресурсов компьютерных систем и сетей
Защита информационных ресурсов компьютерных систем и сетей Громадянське суспільство та політичні партії. (Лекция 3)
Громадянське суспільство та політичні партії. (Лекция 3) Презентация "Как начиналась галерея" - скачать презентации по МХК
Презентация "Как начиналась галерея" - скачать презентации по МХК Губка Боб или Спанч Боб - это мультяшный герой, живущий на дне океана в городе Бикини Боттом
Губка Боб или Спанч Боб - это мультяшный герой, живущий на дне океана в городе Бикини Боттом . Лечение угревой болезни
. Лечение угревой болезни Имя существительное
Имя существительное Закономерности, принципы и методы управления персоналом
Закономерности, принципы и методы управления персоналом Расчет токов КЗ в программном комплексе АРМ СРЗА ПК Бриз
Расчет токов КЗ в программном комплексе АРМ СРЗА ПК Бриз Урок 25 Состав числа 11 и соответствующие случаи вычитания
Урок 25 Состав числа 11 и соответствующие случаи вычитания  Выключатель подачи топлива. Чертёж
Выключатель подачи топлива. Чертёж Графические возможности Delphi
Графические возможности Delphi Политическая мода и стиль
Политическая мода и стиль Свод знаний по управлению проектами. PMBOK – Project Management Body of Knowledge
Свод знаний по управлению проектами. PMBOK – Project Management Body of Knowledge Патриарх сибирского пейзажа Кондратий Белов
Патриарх сибирского пейзажа Кондратий Белов WM HSG Special Options (룸콘 특수기능). Настройка котла
WM HSG Special Options (룸콘 특수기능). Настройка котла Взаимная индукция. Энергия магн.поля
Взаимная индукция. Энергия магн.поля Нормативно-правовое и нормативно-техническое регулирование в строительстве
Нормативно-правовое и нормативно-техническое регулирование в строительстве Режимы налогообложения. Задание 6
Режимы налогообложения. Задание 6 Основные термины электроники. Полупроводниковые элементы. Полупроводниковые выпрямители
Основные термины электроники. Полупроводниковые элементы. Полупроводниковые выпрямители Доходы государства
Доходы государства Разработка и монтаж электронного блока утечки бытового газа для одного подьезда на базе микроконтроллера Atmega8
Разработка и монтаж электронного блока утечки бытового газа для одного подьезда на базе микроконтроллера Atmega8 Электрощит питания судов с берега. Стартерный пуск судового дизель-генератора. (Билет 13)
Электрощит питания судов с берега. Стартерный пуск судового дизель-генератора. (Билет 13) Презентация Стратегия развития Федеральной таможенной службы до 2020 г
Презентация Стратегия развития Федеральной таможенной службы до 2020 г History of computer development
History of computer development Презентация Цели, задачи и функции государственного управления на современном этапе
Презентация Цели, задачи и функции государственного управления на современном этапе  Презентация "Введение в макроэкономику" - скачать презентации по Экономике
Презентация "Введение в макроэкономику" - скачать презентации по Экономике Олимпийское движение как социальный феномен
Олимпийское движение как социальный феномен Расчет и определение оптимальной комплектации водосточной системы
Расчет и определение оптимальной комплектации водосточной системы