Содержание
- 2. Позиционные задачи Задачи, решаемые в начертательной геометрии делятся на метрические и позиционные. В метрических задачах определяются
- 3. Пересечение поверхности плоскостью Линия, которая получается от пересечения поверхности с плоскостью, является плоской кривой, лежащей в
- 4. Пересечение гранной поверхности плоскостью
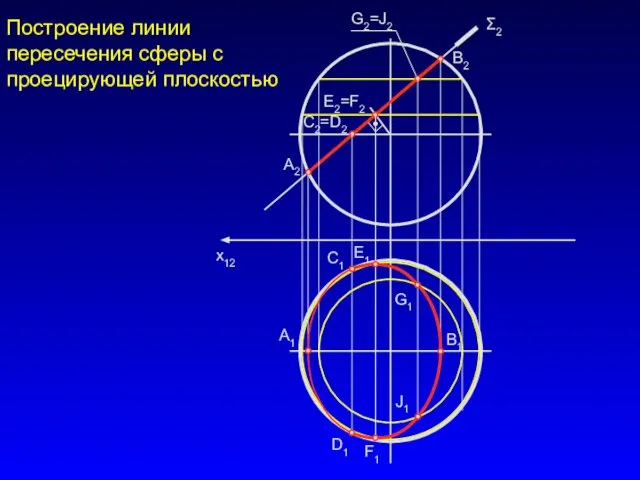
- 11. x12 Σ2 Построение линии пересечения сферы с проецирующей плоскостью А1 В2 В1 А2 С2=D2 C1 D1
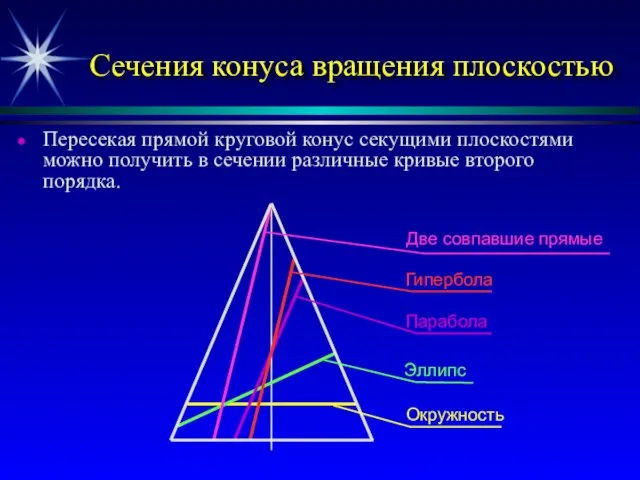
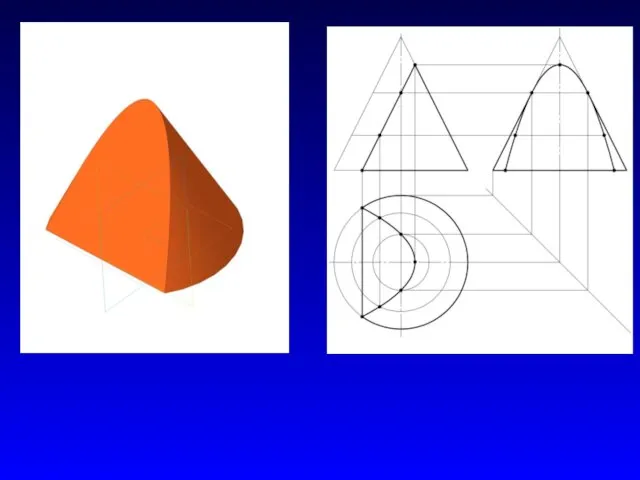
- 12. Сечения конуса вращения плоскостью Пересекая прямой круговой конус секущими плоскостями можно получить в сечении различные кривые
- 18. Пересечение линии с поверхностью Построение точек пересечения линии, с какой – либо поверхностью выполняется с помощью
- 19. Пересечение линии с поверхностью В качестве вспомогательной поверхности Θ обычно используют: плоскость (если заданная линия является
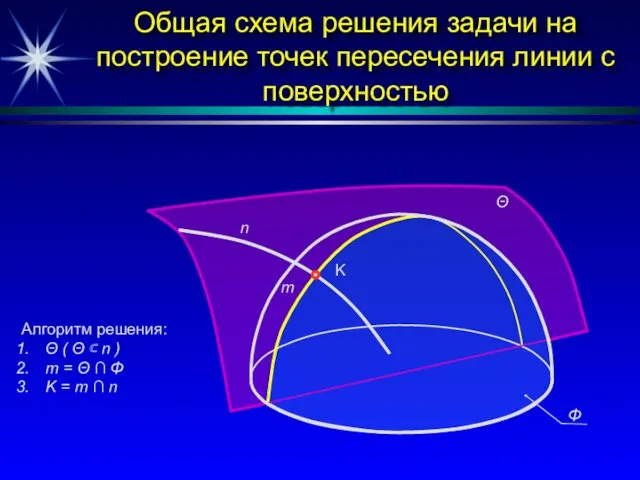
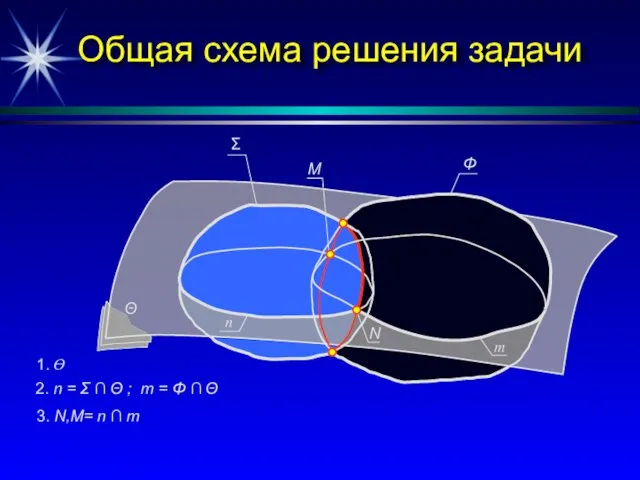
- 20. Общая схема решения задачи на построение точек пересечения линии с поверхностью n K m Θ Φ
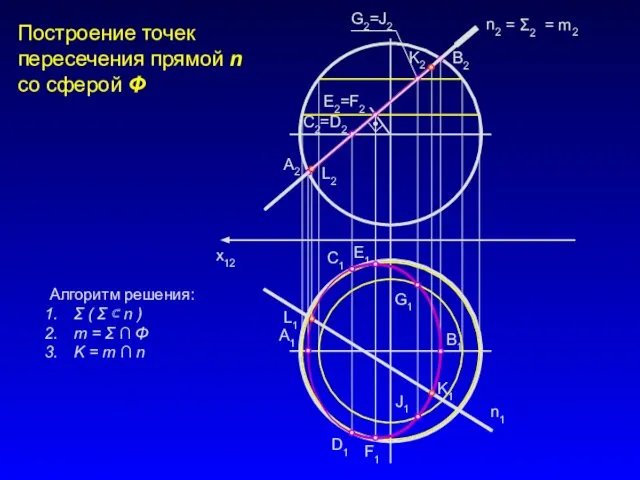
- 21. x12 n2 Построение точек пересечения прямой n со сферой Φ А1 В2 В1 А2 С2=D2 C1
- 22. Взаимное пересечение поверхностей В начертательной геометрии линию пересечения двух поверхностей находят с помощью приёма, который называется
- 23. Общая схема решения задачи Θ 1. Ө 2. n = Σ ∩ Θ ; m =
- 24. Общая схема решения задачи 1. Обе заданные поверхности пересекаются вспомогательной поверхностью Θ. В качестве вспомогательной чаще
- 25. Общая схема решения задачи Выбор и расположение секущих вспомогательных поверхностей определяется следующими обстоятельствами: 1) желательно, чтобы
- 26. Метод вспомогательных секущих плоскостей Этот способ применяют для построения точек линии пересечения двух поверхностей тогда, когда
- 27. Метод вспомогательных секущих плоскостей Среди точек линии пересечения есть такие, которые выделяются своим особым положением среди
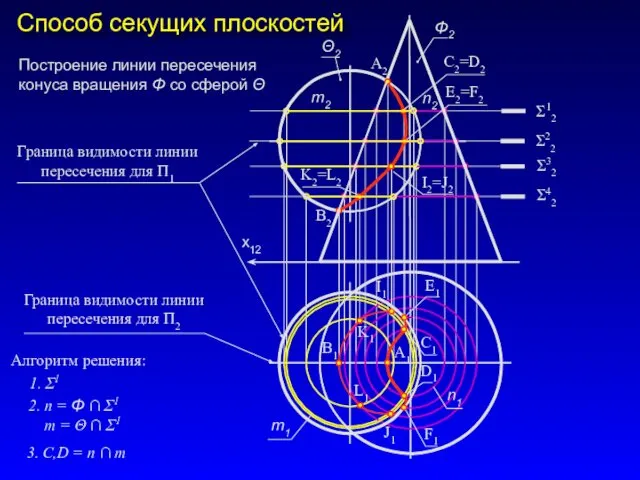
- 28. Способ секущих плоскостей А2 В2 В1 А1 Σ12 Σ22 Σ32 Σ42 I1 J1 K1 L1 Построение
- 30. Скачать презентацию




















 Шрифт чертежный. Написание прописных и строчных букв
Шрифт чертежный. Написание прописных и строчных букв Пересечение поверхности плоскостью
Пересечение поверхности плоскостью Тени в угловом интерьере от искусственного источника света
Тени в угловом интерьере от искусственного источника света Строительный чертеж
Строительный чертеж Архитектурная графика
Архитектурная графика Строительные чертежи
Строительные чертежи Пересечение многогранника с плоскостью
Пересечение многогранника с плоскостью Угловая и фронтальная перспектива
Угловая и фронтальная перспектива Чертежная грамотность
Чертежная грамотность Совершенствование организации технического обслуживания и ремонта техники в ООО Кипенская СХТ Ленинградской области
Совершенствование организации технического обслуживания и ремонта техники в ООО Кипенская СХТ Ленинградской области Аксонометрия. Однокартинный чертеж, обладающий свойствами наглядности и обратимости
Аксонометрия. Однокартинный чертеж, обладающий свойствами наглядности и обратимости Проецирование. Технический рисунок. Альбом
Проецирование. Технический рисунок. Альбом Соединения деталей
Соединения деталей Взаимное пересечение кривых поверхностей
Взаимное пересечение кривых поверхностей Создание сборочного чертежа редуктора
Создание сборочного чертежа редуктора Суммарные отклонения и допуски формы и расположения поверхностей в пределах нормируемого участка (ГОСТ 24642-81)
Суммарные отклонения и допуски формы и расположения поверхностей в пределах нормируемого участка (ГОСТ 24642-81) Поверхности. Задание поверхности на комплексном чертеже (лекция 7)
Поверхности. Задание поверхности на комплексном чертеже (лекция 7) Сечение геометрических тел плоскостями (1 часть)
Сечение геометрических тел плоскостями (1 часть) Совершенствование ремонта техники с разработкой приспособления для отвинчивания пробок наконечников рулевых тяг
Совершенствование ремонта техники с разработкой приспособления для отвинчивания пробок наконечников рулевых тяг Аксонометрические проекции
Аксонометрические проекции Аксонометрические проекции плоских фигур
Аксонометрические проекции плоских фигур Шрифт чертежный
Шрифт чертежный Чтение и выполнение чертежей деталей
Чтение и выполнение чертежей деталей Объёмные геометрические тела
Объёмные геометрические тела Технический рисунок
Технический рисунок Роль чертежей в жизни человека
Роль чертежей в жизни человека Элементы, конструктивные схемы и классификация зданий
Элементы, конструктивные схемы и классификация зданий Унификация, типизация и стандартизация в проектировании и строительстве
Унификация, типизация и стандартизация в проектировании и строительстве