Содержание
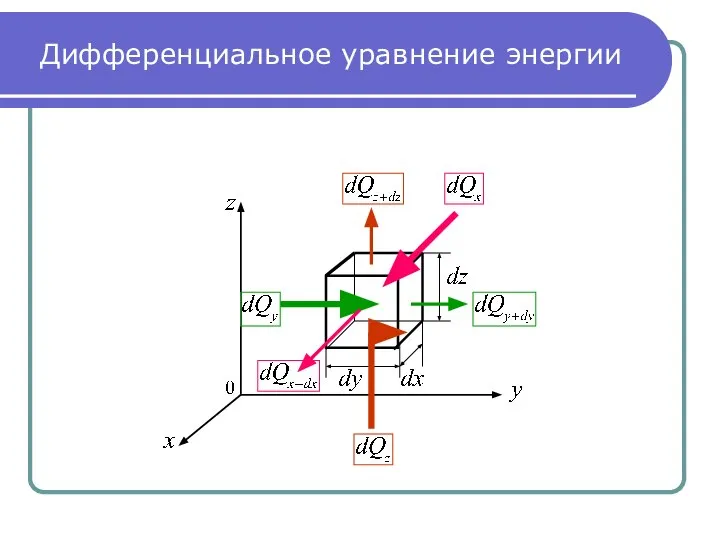
- 2. Дифференциальное уравнение энергии Выведем дифференциальное уравнение температурного поля в движущейся жидкости. Допущения: Жидкость однородна и изотропна;
- 3. Дифференциальное уравнение энергии
- 4. Дифференциальное уравнение энергии Формально дифференциальное уравнение энергии будет таким же как и при отсутствии конвекции: (1)
- 5. Дифференциальное уравнение энергии Плотность теплового потока при конвективном теплообмене:
- 6. Дифференциальное уравнение энергии Отсюда проекции плотности теплового потока на координатные оси:
- 7. Дифференциальное уравнение энергии Тогда уравнение (1) примет вид: (2)
- 8. Дифференциальное уравнение энергии Для несжимаемых жидкостей:
- 9. . . Дифференциальное уравнение энергии Тогда уравнение (2) примет вид: (3)
- 10. . . Дифференциальное уравнение энергии Уравнение (3) также можно представить в виде: (4)
- 11. . . Дифференциальное уравнение энергии Левая часть уравнения (4) есть полная производная от температуры по времени:
- 12. . . Дифференциальное уравнение энергии Член характеризует изменение температуры в отдельных точках жидкости (локальное изменение температуры)
- 13. . . Дифференциальное уравнение энергии Член характеризует изменение температуры при переходе от точки к точке (конвективное
- 14. Дифференциальное уравнение энергии Обозначим:
- 15. Дифференциальное уравнение энергии Тогда уравнение энергии можно записать в виде: (5)
- 16. Дифференциальное уравнение энергии При уравнение энергии переходит в уравнение теплопроводности
- 17. Дифференциальные уравнения движения Температурное поле в движущейся жидкости зависит от составляющих скорости. Для того, чтобы система
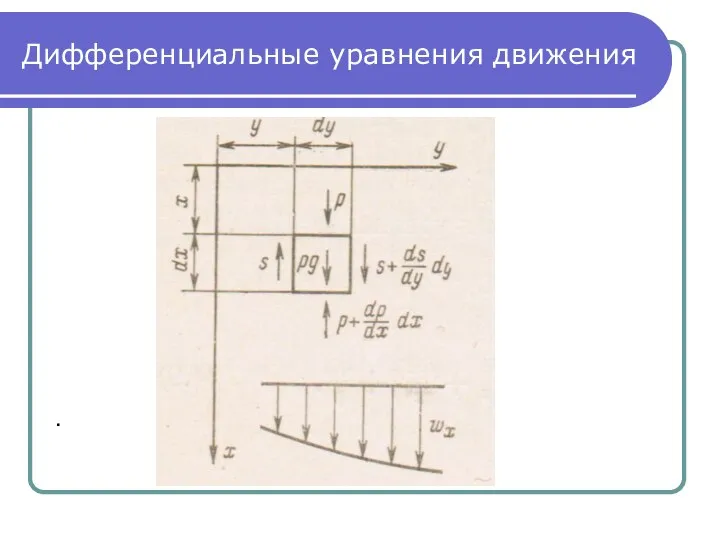
- 18. Дифференциальные уравнения движения Дадим упрощенный вывод дифференциального уравнения движения для случая одномерного течения несжимаемой жидкости. Затем
- 19. Дифференциальные уравнения движения .
- 20. Дифференциальные уравнения движения Вывод основан на втором законе Ньютона: сила равна массе, умноженной на ускорение. Силы,
- 21. Дифференциальные уравнения движения Следовательно, на рассматриваемый элемент жидкости действуют три силы: Сила тяжести; Равнодействующая сил давления;
- 22. Дифференциальные уравнения движения Найдем проекции этих сил на ось Ox. Сила тяжести приложена в центре тяжести
- 23. Дифференциальные уравнения движения Сила давления на верхнюю грань: Сила давления на нижнюю грань:
- 24. Дифференциальные уравнения движения Равнодействующая сил давления равна их алгебраической сумме:
- 25. Дифференциальные уравнения движения С учетом того, что скорость изменяется только в направлении оси Oy, то сила
- 26. Дифференциальные уравнения движения С учетом того, что Получим:
- 27. Дифференциальные уравнения движения Проекция на ось Ox равнодействующей всех сил, приложенных к объему:
- 28. Дифференциальные уравнения движения С другой стороны по второму закону:
- 29. Дифференциальные уравнения движения Приравняв правые части последних уравнений, получим:
- 30. Дифференциальные уравнения движения В случае трехмерного движения несжимаемой жидкости с постоянными физическими параметрами поле скоростей опишется
- 31. Дифференциальные уравнения движения Для оси Ox:
- 32. Дифференциальные уравнения движения Для оси Oy:
- 33. Дифференциальные уравнения движения Для оси Oz:
- 34. Дифференциальные уравнения движения На основании понятия о полной производной члены, стоящие в правой части уравнений можно
- 35. Дифференциальные уравнения движения Для оси Oy:
- 36. Дифференциальные уравнения движения Для оси Oz:
- 37. Дифференциальные уравнения движения Уравнения Навье-Стокса в векторной форме:
- 38. Уравнение сплошности Ранее было установлено, что для несжимаемых жидкостей:
- 40. Скачать презентацию



































 Аттестационная работа. Рабочая программа дополнительного образования. Кружок по физике: Удивительная физика 6 класс
Аттестационная работа. Рабочая программа дополнительного образования. Кружок по физике: Удивительная физика 6 класс Презентация по физике "Производство электрической энергии" - скачать
Презентация по физике "Производство электрической энергии" - скачать  Механические свойства металлов
Механические свойства металлов Элементы специальной теории относительности. Релятивистская динамика
Элементы специальной теории относительности. Релятивистская динамика Материальная точка. Система отсчета
Материальная точка. Система отсчета Золотое правило механики
Золотое правило механики Електропровідність металів та напівпровідників. Закони Ома. Правила Кірхгофа
Електропровідність металів та напівпровідників. Закони Ома. Правила Кірхгофа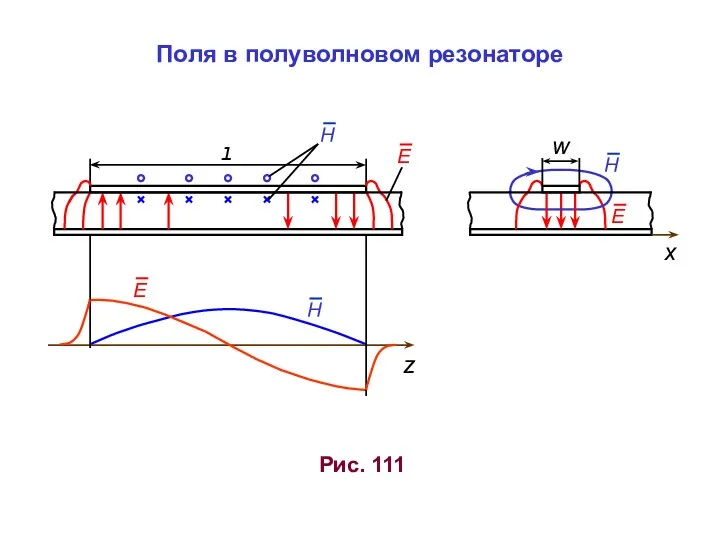 Поля в полуволновом резонаторе
Поля в полуволновом резонаторе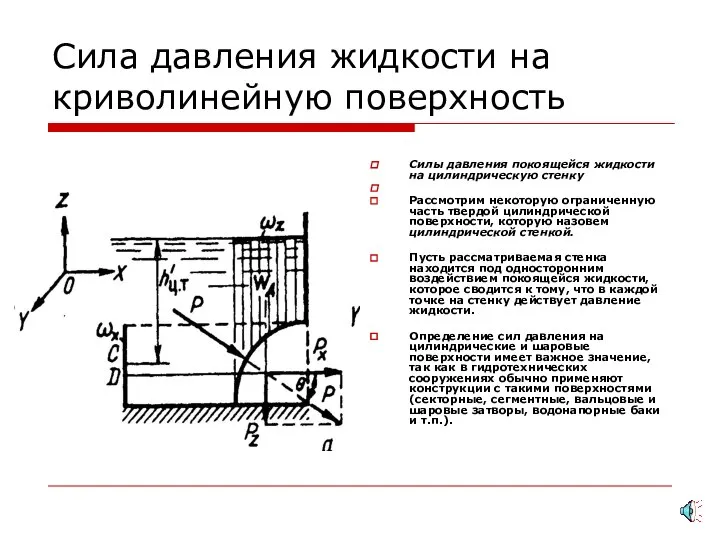 Сила давления жидкости на криволинейную поверхность
Сила давления жидкости на криволинейную поверхность Тепловые явления
Тепловые явления Динамическое проектирование систем стабилизации летательных аппаратов. Исполнительные устройства. Рулевой привод
Динамическое проектирование систем стабилизации летательных аппаратов. Исполнительные устройства. Рулевой привод Трубки газоразрядные
Трубки газоразрядные Постоянный ток
Постоянный ток Podstawowe pojęcia z zakresu RADIOMETRII
Podstawowe pojęcia z zakresu RADIOMETRII Кросс-дисциплинарный межфакультетский учебный модуль «КВАНТУМ»
Кросс-дисциплинарный межфакультетский учебный модуль «КВАНТУМ» Механическая работа
Механическая работа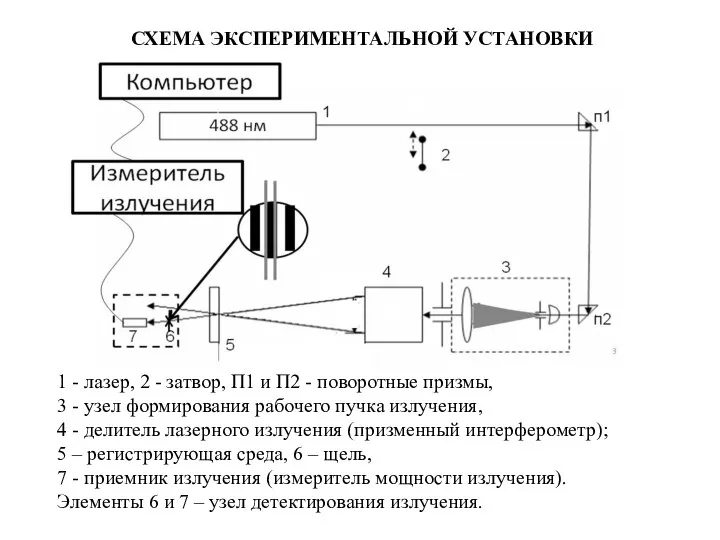 Схема экспериментальной установки
Схема экспериментальной установки Исследование цикла Червякова с целью повышения эффективности ДВС
Исследование цикла Червякова с целью повышения эффективности ДВС Тепломассообмен. Сложный теплообмен
Тепломассообмен. Сложный теплообмен Диффузия в газах, жидкостях и твердых телах.
Диффузия в газах, жидкостях и твердых телах. Механические колебания
Механические колебания Презентация по физике "Теплопередача вокруг нас" - скачать
Презентация по физике "Теплопередача вокруг нас" - скачать  УРОК ФИЗИКИ 8 КЛАСС Учитель физики МОУ СОШ№4 г.Миньяра УСКОВА СВЕТЛАНА СЕМЁНОВНА
УРОК ФИЗИКИ 8 КЛАСС Учитель физики МОУ СОШ№4 г.Миньяра УСКОВА СВЕТЛАНА СЕМЁНОВНА Дифракция света. Дифракционная решётка.
Дифракция света. Дифракционная решётка. Физические основы работы светодиодов
Физические основы работы светодиодов Основные свойства диэлектриков. Сегнетоэлектрики
Основные свойства диэлектриков. Сегнетоэлектрики Определение гамма-излучения в Челябинском городском бору
Определение гамма-излучения в Челябинском городском бору Относительность механического движения
Относительность механического движения