Содержание
- 2. Тема 12 Циркуляция вектора магнитной индукции
- 3. Тема 12. Циркуляция вектора магнитной индукции 12.1. Теорема о циркуляции 12.2. Магнитное поле соленоида 12.3. Магнитное
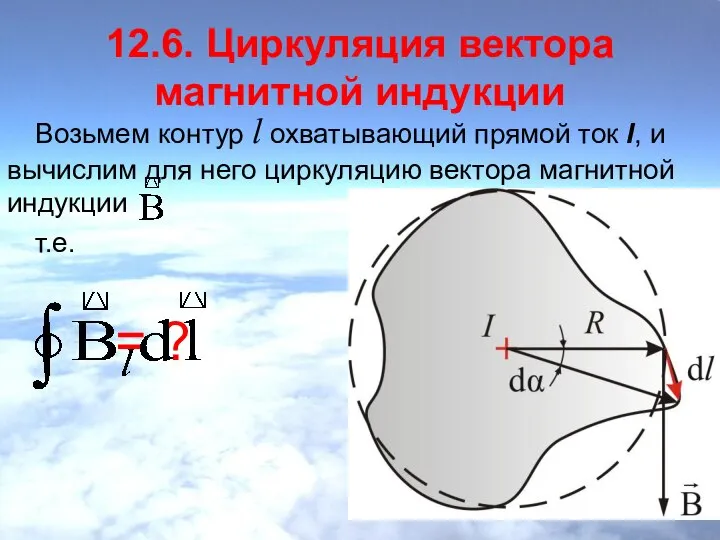
- 4. 12.6. Циркуляция вектора магнитной индукции Возьмем контур l охватывающий прямой ток I, и вычислим для него
- 5. Вначале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В
- 6. Теорема о циркуляции вектора : циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную
- 7. Иначе обстоит дело, если ток не охватывается контуром В этом случае при обходе радиальная прямая поворачивается
- 8. Итак, где I – ток, охваченный контуром L. Эта формула справедлива и для тока произвольной формы,
- 9. Если контур охватывает несколько токов, то (2.6.3) т.е. циркуляция вектора равна алгебраической сумме токов, охваченных контуром
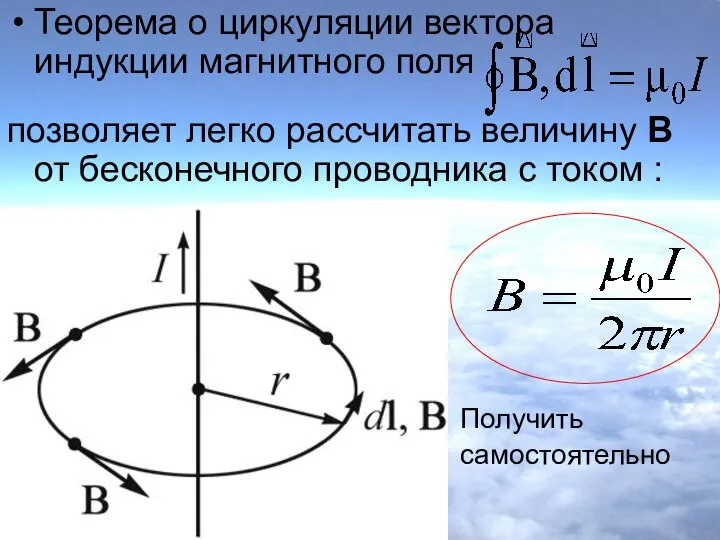
- 10. Теорема о циркуляции вектора индукции магнитного поля позволяет легко рассчитать величину В от бесконечного проводника с
- 11. Итак, циркуляция вектора магнитной индукции отлична от нуля, если контур охватывает ток Сравните с циркуляцией вектора
- 12. Линии напряженности электрического поля начинаются и заканчиваются на зарядах. А магнитных зарядов в природе нет. Опыт
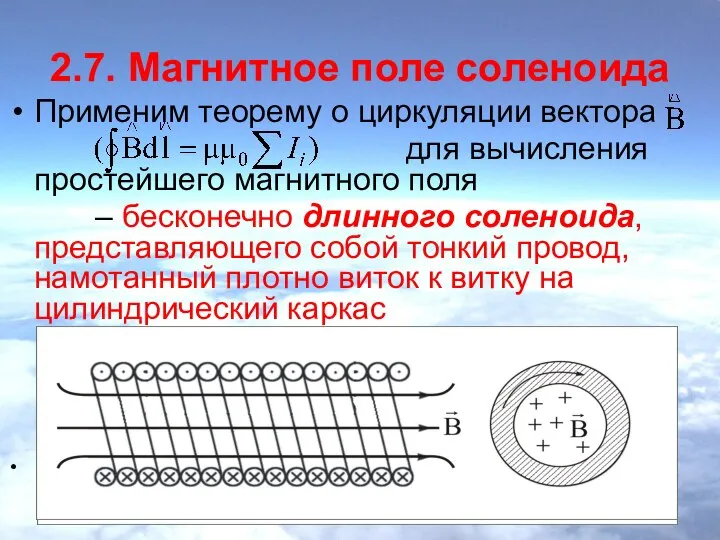
- 13. 2.7. Магнитное поле соленоида Применим теорему о циркуляции вектора для вычисления простейшего магнитного поля – бесконечно
- 14. Соленоид можно представить в виде системы одинаковых круговых токов с общей прямой осью. Бесконечно длинный соленоид
- 15. Из параллельности вектора оси соленоида вытекает, что поле как внутри, так и вне соленоида должно быть
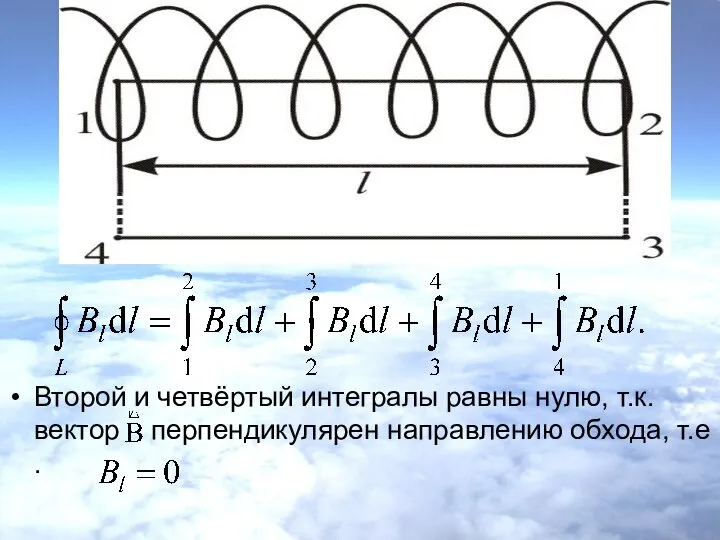
- 16. Второй и четвёртый интегралы равны нулю, т.к. вектор перпендикулярен направлению обхода, т.е .
- 17. Возьмём участок 3–4 – на большом расстоянии от соленоида, где поле стремится к нулю; и пренебрежём
- 18. магнитная индукция внутри соленоида Вне соленоида: и , т.е. . Бесконечно длинный соленоид аналогичен плоскому конденсатору
- 19. Если же катушка короткая, что обычно и бывает на практике, то магнитная индукция в любой точке
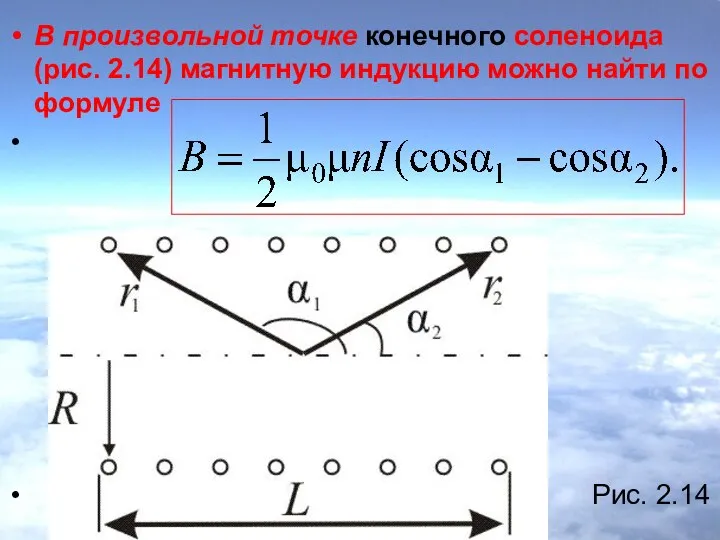
- 20. В произвольной точке конечного соленоида (рис. 2.14) магнитную индукцию можно найти по формуле Рис. 2.14
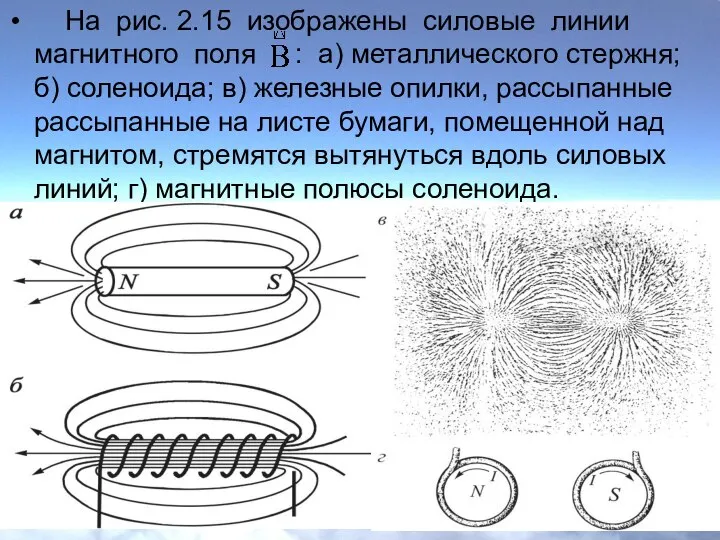
- 21. На рис. 2.15 изображены силовые линии магнитного поля : а) металлического стержня; б) соленоида; в) железные
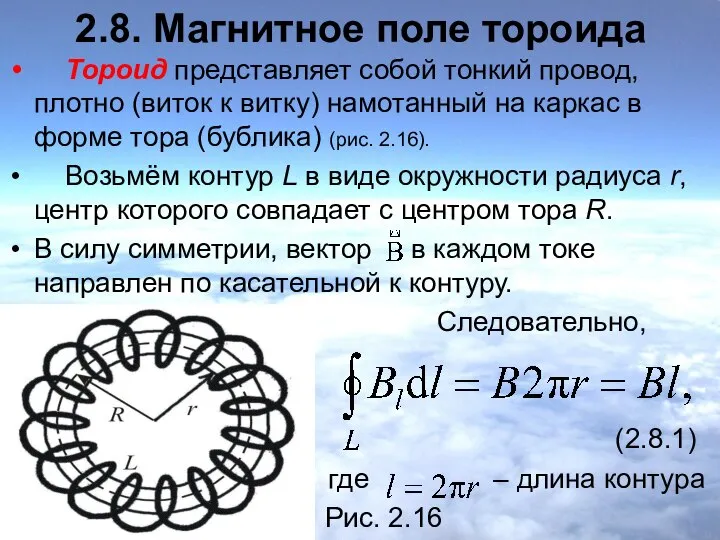
- 22. 2.8. Магнитное поле тороида Тороид представляет собой тонкий провод, плотно (виток к витку) намотанный на каркас
- 23. Если контур проходит внутри тороида, он охватывает ток (n – число витков на единицу длины). Тогда,
- 24. Для тороида, где радиус тора намного больше радиуса витка, отношение , тогда магнитное поле тора В
- 25. Движение проводника в магнитном поле
- 26. Работа силы Ампера:
- 27. За счет чего выполняется работа?!
- 28. Работа силы Ампера:
- 29. Работа силы Ампера определяется двумя факторами: 1-наличием тока в проводнике, 2-изменением магнитного потока
- 30. 2.9. Работа по перемещению проводника с током в магнитном поле Рассмотрим контур с током, образованный неподвижными
- 31. Рис. 2.17 На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо: Пусть
- 32. Итак, (2.9.1) Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток,
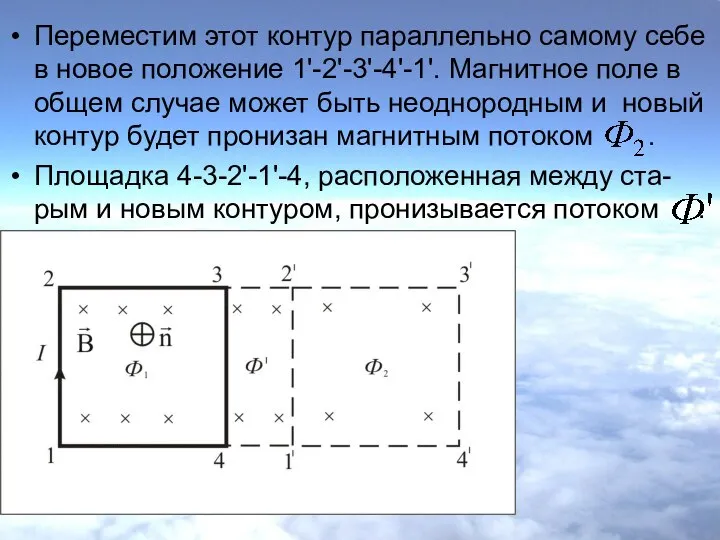
- 33. Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле. Рассмотрим прямоугольный контур
- 34. Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может
- 35. Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой
- 36. Провод 1–2 перерезает поток ( ), но движется против сил действия магнитного поля. Тогда общая работа
- 37. Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на
- 38. Соотношение (2.9.5), выведенное нами для простейшего случая, остаётся справедливым для контура любой формы в произвольном магнитном
- 39. 2.10. Эффект Холла Одним из проявлений магнитной составляющей силы Лоренца в веществе служит эффект, обнаруженный в
- 40. Эффект Холла Обусловлен действием Лоренцевой силы на свободные заряды в проводнике. Представим себе проводник в виде
- 41. Это позволяет экспериментально определить знак носителя заряда в проводнике. При равной концентрации носителей заряда обоих знаков
- 42. Перераспределение зарядов прекратится, когда сила qEx уравновесит лоренцеву силу, т.е. или Плотность тока , отсюда .
- 43. холловская разность потенциалов Где – коэффициент Холла.
- 44. Исследования ЭДС Холла привели к удивительным выводам: Металлы могут обладать проводимостью р –типа (Zn, Cd –
- 45. Из формулы 10.6.3 можно вывести число носителей заряда. (10.6.4) Итак, измерение Холловской разности потенциалов позволяет определить:
- 52. Скачать презентацию






































 Использование открытия радиоактивности: энергия разрушения и энергия созидания.
Использование открытия радиоактивности: энергия разрушения и энергия созидания. Материальная точка. Система отсчета. Движение
Материальная точка. Система отсчета. Движение Введение в профессию
Введение в профессию Элементтердің периодтық жүйесі және оның физикалық түсіндірілуі. Паули принципі. Хунд ережесі
Элементтердің периодтық жүйесі және оның физикалық түсіндірілуі. Паули принципі. Хунд ережесі Fizika
Fizika Двухтактный преобразователь постоянного напряжения с трансформаторной развязкой
Двухтактный преобразователь постоянного напряжения с трансформаторной развязкой ИК-спектроскопия. История возникновения
ИК-спектроскопия. История возникновения Электростатика. Электродинамика
Электростатика. Электродинамика Магниты на основе современных массивных высокотемпературных сверхпроводников
Магниты на основе современных массивных высокотемпературных сверхпроводников Сила трения
Сила трения Презентация по физике "Рождение электрон-позитронных пар и поглощение гамма-квантов" - скачать
Презентация по физике "Рождение электрон-позитронных пар и поглощение гамма-квантов" - скачать  Электрическая система. (Лекция 1)
Электрическая система. (Лекция 1) Волновые передачи
Волновые передачи Капиллярность. Капиллярные явления
Капиллярность. Капиллярные явления Первый закон термодинамики
Первый закон термодинамики Размерные цепи
Размерные цепи Types of radio waves
Types of radio waves Многоэлектронные атомы. Взаимодействие атомов с излучением
Многоэлектронные атомы. Взаимодействие атомов с излучением Джерела і приймачі світла. Поглощеня і розсіювання світла
Джерела і приймачі світла. Поглощеня і розсіювання світла Презентация по физике "Невесомость физика" - скачать
Презентация по физике "Невесомость физика" - скачать  Инфракрасное излучение
Инфракрасное излучение Биосенсоры
Биосенсоры Автоматика. Типовые звенья САУ и их свойства
Автоматика. Типовые звенья САУ и их свойства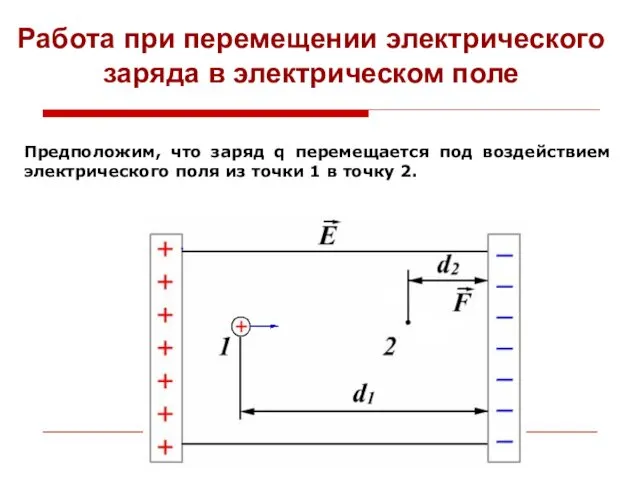 Работа при перемещении электрического заряда в электрическом поле
Работа при перемещении электрического заряда в электрическом поле Физический маятник
Физический маятник Презентация Тепловое действие тока
Презентация Тепловое действие тока Экспериментальные задачи по физике в формировании УУД. Двигатель Стирлинга
Экспериментальные задачи по физике в формировании УУД. Двигатель Стирлинга Механическое движение тела
Механическое движение тела