Содержание
- 2. Кинематикой называется раздел теоретической механики, в котором изучается движение материальных тел без учета действия сил, вызывающих
- 3. Движением называется изменение положения одних тел по отношению к другим телам. Тело, по отношению к которому
- 4. По виду движущихся объектов кинематика подразделяется на кинематику точки и кинематику твердого тела. Точкой считается тело,
- 5. КИНЕМАТИКА ТОЧКИ
- 6. План Способы задания движения точки Определение скорости и ускорения при векторном способе задания движения Определение скорости
- 7. Задачей кинематики точки является определение кинематических характеристик движения точки – траекторий, скоростей и ускорений. Для этого
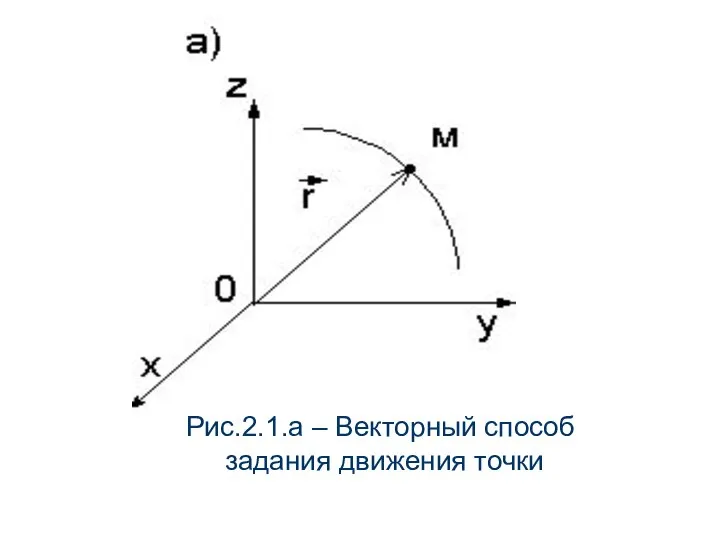
- 8. 2.1.1 Способы задания движения точки Рассмотрим три способа задания движения точки: векторный, координатный и естественный. При
- 9. Рис.2.1.а – Векторный способ задания движения точки
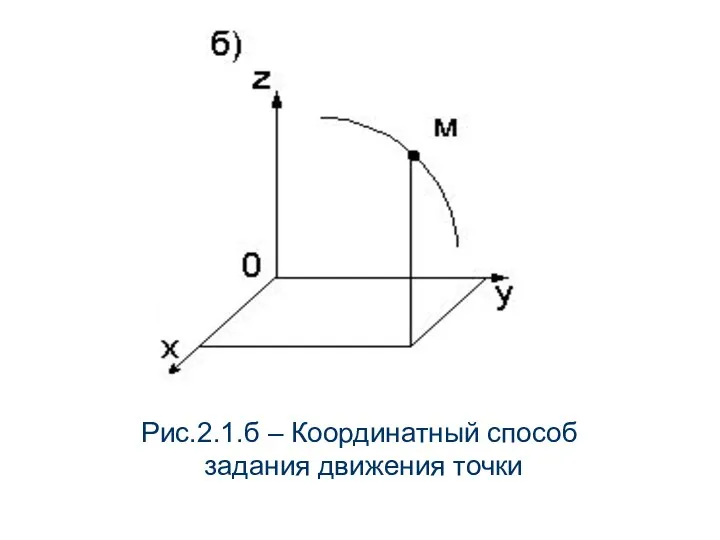
- 10. При координатном способе задаются зависимости координат точки (рис.2.1,б) от времени: (2.2) Данные уравнения позволяют в любой
- 11. Рис.2.1.б – Координатный способ задания движения точки
- 12. Уравнения (2.2) являются уравнениями траектории точки в параметрической форме. Для получения уравнения траектории в координатной форме
- 13. Решение. Из первого уравнения: t=x/2, подставляя во второе, получим: у=х2/4; поскольку х и у положительны, то
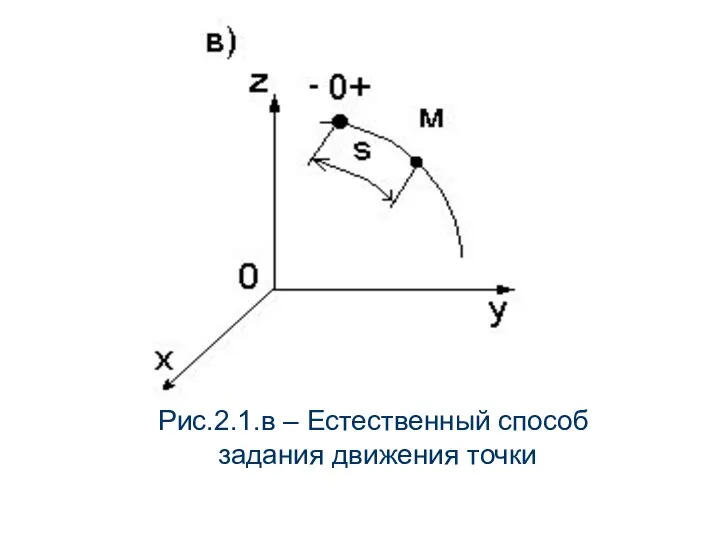
- 14. При естественном способе задания движения (рис.2.1,в) задается траектория, начало отсчета и направление, а также закон движения
- 15. Рис.2.1.в – Естественный способ задания движения точки
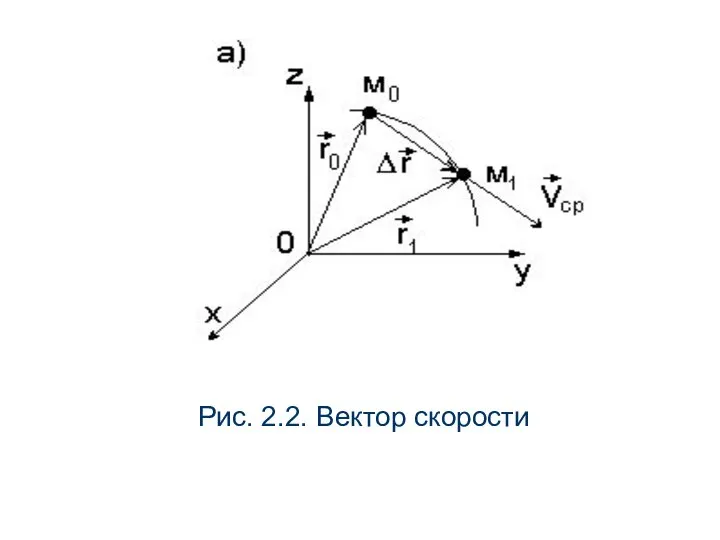
- 16. Векторный способ Вектор скорости Одной из важнейших кинематических характеристик движения является скорость, она характеризует быстроту перемещения
- 17. Рис. 2.2. Вектор скорости
- 18. За время t1 - t0 радиус-вектор изменится на величину . Вектор называется вектором перемещения. Средней скоростью
- 19. Мгновенной скоростью называется предел,к которому стремится средняя скорость, если промежуток времени стремится к нулю (2.5) то
- 20. Вектор ускорения Ускорение характеризует изменение скорости. Пусть в момент времени t0 точка имеет скорость а в
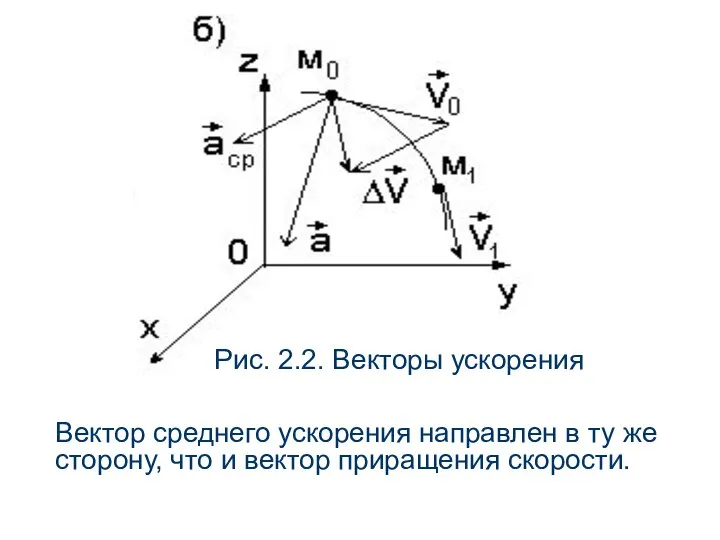
- 21. Рис. 2.2. Векторы ускорения Вектор среднего ускорения направлен в ту же сторону, что и вектор приращения
- 22. Мгновенным ускорением называется предел, к которому стремится среднее ускорение, если промежуток времени стремится к нулю: то
- 23. Определение скорости и ускорения при координатном способе задания движения Введем единичные орты осей координат - (рис.2.3),
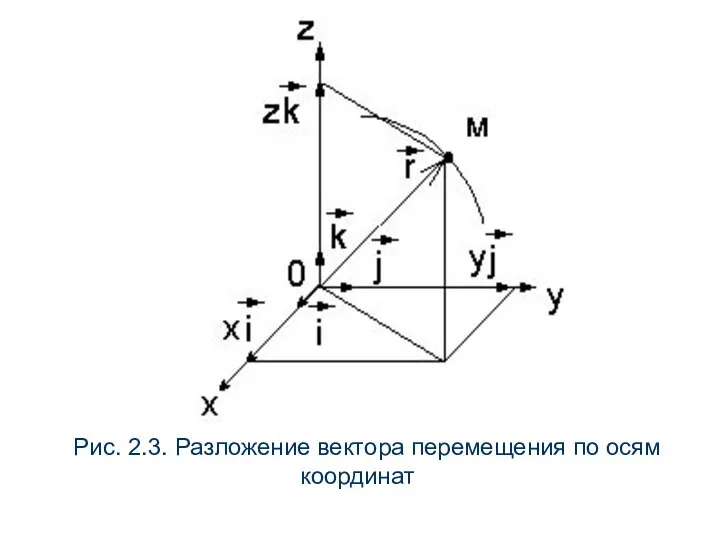
- 24. Рис. 2.3. Разложение вектора перемещения по осям координат
- 25. Левые части выражений (б) и (в) равны, поэтому, получим выражения для проекций скорости на оси координат:
- 26. Аналогично можно получить формулы для определения проекций на оси координат и модуля ускорения: (2.10) (2.11) Модуль
- 27. Пример 2 . По уравнениям, приведенным в примере 1 (Движение точки задано уравнениями: x=2t, y=t2) найти
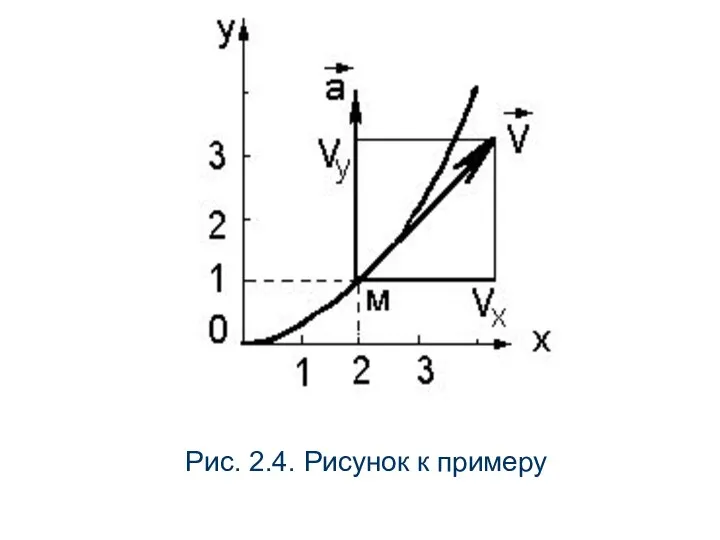
- 28. Рис. 2.4. Рисунок к примеру
- 29. Модуль скорости: Откладывая из точки М в масштабе по осям Х и У значения Vx=2, Vy=2t=2,
- 30. Определение скорости и ускорения при естественном способе задания движения При данном способе скорость и ускорение находятся
- 31. Рис. 2.5. Естественные оси координат
- 32. Проекция скорости на ось τ: (2.12) то есть равна производной по времени от закона движения точки
- 33. Проекция ускорения на ось τ называется касательным ускорением и определяется по формуле (2.13) (2.14) Проекция ускорения
- 34. Пример 3. По условию предыдущего примера (Движение точки задано уравнениями: x=2t, y=t2) найти касательное и нормальное
- 36. Скачать презентацию


























 Модернизация системы главной понизительной подстанции механического завода
Модернизация системы главной понизительной подстанции механического завода Силы в природе
Силы в природе Устная разминка по теме: «Внутренняя энергия» 8кл
Устная разминка по теме: «Внутренняя энергия» 8кл Волны. Лекция 13
Волны. Лекция 13 Особенности создания гиперзвуковых летательных аппаратов (ГЛА)
Особенности создания гиперзвуковых летательных аппаратов (ГЛА) №37 01.02.2022
№37 01.02.2022 Физические приборы
Физические приборы Топологии импульсных преобразователей
Топологии импульсных преобразователей Открытие нейтронов и протонов
Открытие нейтронов и протонов Итоги диагностики качества предметного обучения по физике в 10 классе Методист по физике ГБОУ МЦ ДОгМ Нугаева Нина Петровна
Итоги диагностики качества предметного обучения по физике в 10 классе Методист по физике ГБОУ МЦ ДОгМ Нугаева Нина Петровна  Физики и деньги Выполнил: ученик 7класса МОУ «Берёзовская СОШ» п. Канифольный Савин Алексей Руководитель: учитель физики Савина
Физики и деньги Выполнил: ученик 7класса МОУ «Берёзовская СОШ» п. Канифольный Савин Алексей Руководитель: учитель физики Савина Скорость движения жидкости как сплошной среды
Скорость движения жидкости как сплошной среды Уравнения состояния термодинамических систем. Лекция № 12
Уравнения состояния термодинамических систем. Лекция № 12 Иследовательская работа по теме: Определение КПД котельной
Иследовательская работа по теме: Определение КПД котельной  Строение атома. Планетарная модель атома
Строение атома. Планетарная модель атома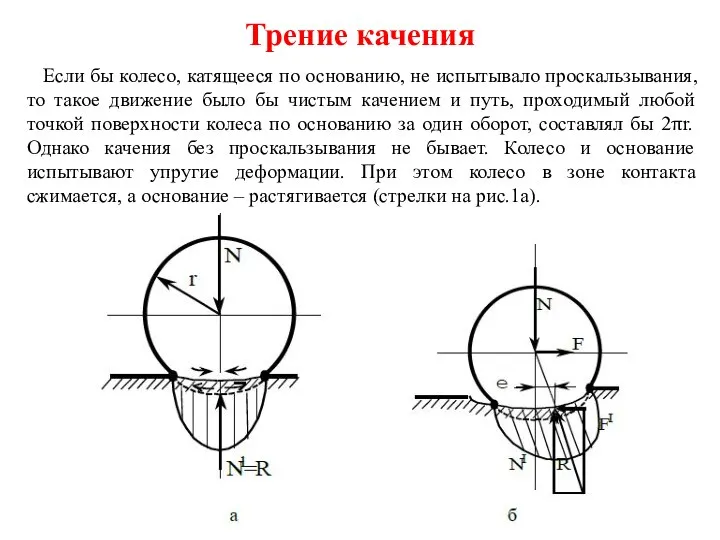 Трение качения
Трение качения Джерела і приймочі світла. Поглощеніе і розсіювання світла
Джерела і приймочі світла. Поглощеніе і розсіювання світла Презентация Движение по окружности Движение по окружности
Презентация Движение по окружности Движение по окружности  Энергетические ресурсы Мирового океана
Энергетические ресурсы Мирового океана Высокоэнергетические материалы в системах детонационной автоматики аэрокосмических аппаратов
Высокоэнергетические материалы в системах детонационной автоматики аэрокосмических аппаратов Движение с постоянным ускорением
Движение с постоянным ускорением Методы синтеза коллоидных кристаллов. (Лекция 13)
Методы синтеза коллоидных кристаллов. (Лекция 13) Силы в механике
Силы в механике Ремонт деталей пластическим деформированием
Ремонт деталей пластическим деформированием Международные системы мер длины: история и современность Автор: ученик 5 «Б» класса МОУ «СОШ № 43» Афанасьев Илья Учитель Дрынко
Международные системы мер длины: история и современность Автор: ученик 5 «Б» класса МОУ «СОШ № 43» Афанасьев Илья Учитель Дрынко Патент на изобретение. На примере хроматографа
Патент на изобретение. На примере хроматографа Импульс тела. Закон сохранения импульса. Реактивное движение
Импульс тела. Закон сохранения импульса. Реактивное движение Механика жидкости и газа
Механика жидкости и газа