Содержание
- 2. ВИДЫ И ПРИЗНАКИ КОЛЕБАНИЙ Для колебаний характерно: превращение одного вида энергии в другую – кинетической в
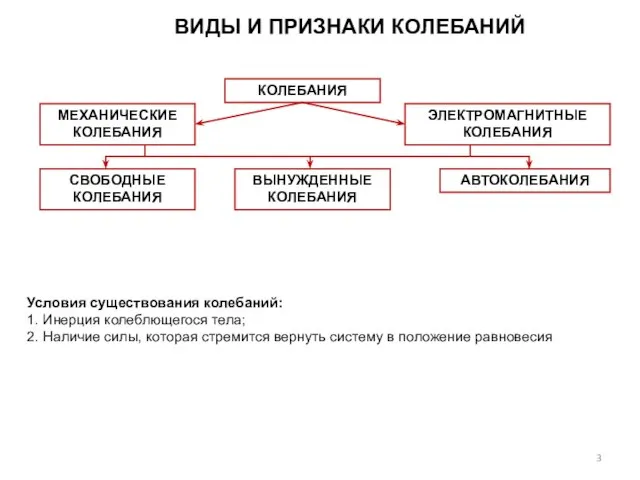
- 3. ВИДЫ И ПРИЗНАКИ КОЛЕБАНИЙ Условия существования колебаний: 1. Инерция колеблющегося тела; 2. Наличие силы, которая стремится
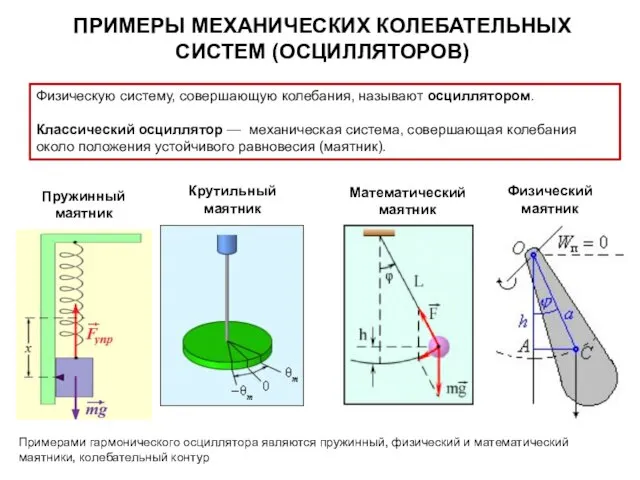
- 4. ПРИМЕРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ (ОСЦИЛЛЯТОРОВ) Пружинный маятник Физический маятник Крутильный маятник Математический маятник Физическую систему, совершающую
- 5. СВОБОДНЫЕ КОЛЕБАНИЯ Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при
- 6. Формула (кинематическое уравнение) гармонического колебания х – смещение в данный момент времени, расстояние материальной точки от
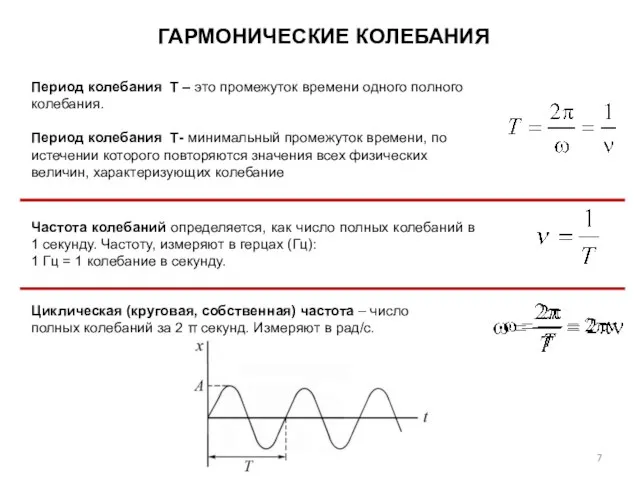
- 7. Период колебания Т – это промежуток времени одного полного колебания. Период колебания Т- минимальный промежуток времени,
- 8. Амплитуда скорости гармонических колебаний Амплитуда ускорения гармонических колебаний Скорость гармонических колебаний Ускорение гармонических колебаний Смещение описывается
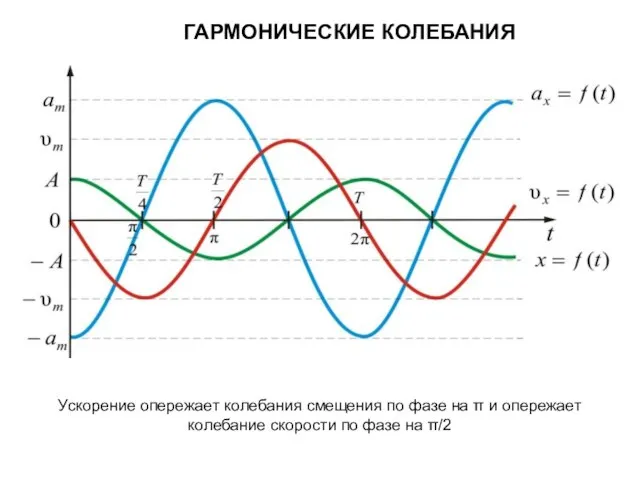
- 9. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ Ускорение опережает колебания смещения по фазе на π и опережает колебание скорости по фазе
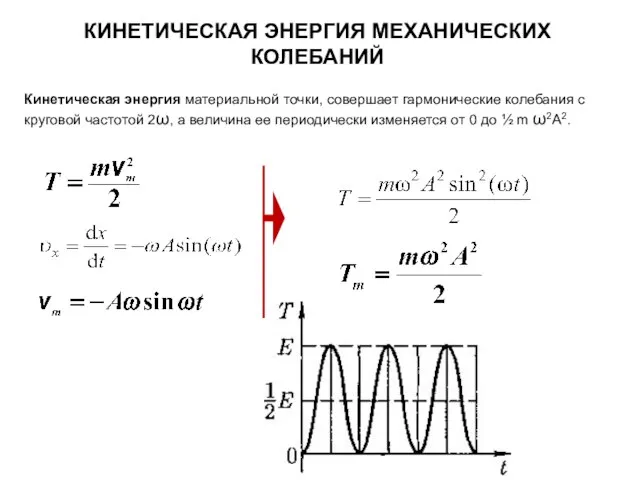
- 10. Кинетическая энергия материальной точки, совершает гармонические колебания с круговой частотой 2ω, а величина ее периодически изменяется
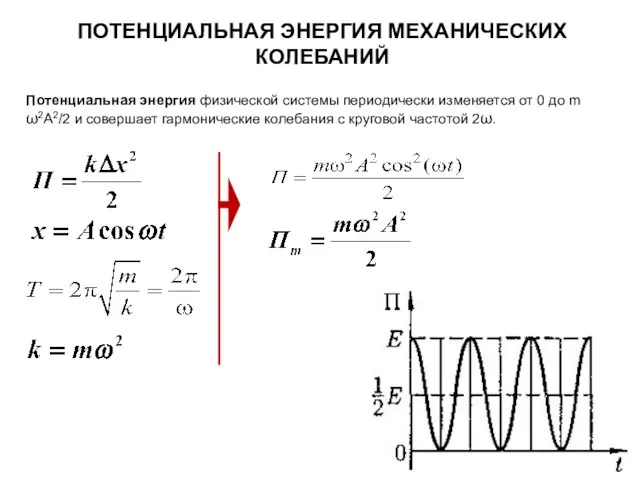
- 11. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ Потенциальная энергия физической системы периодически изменяется от 0 до m ω2A2/2 и
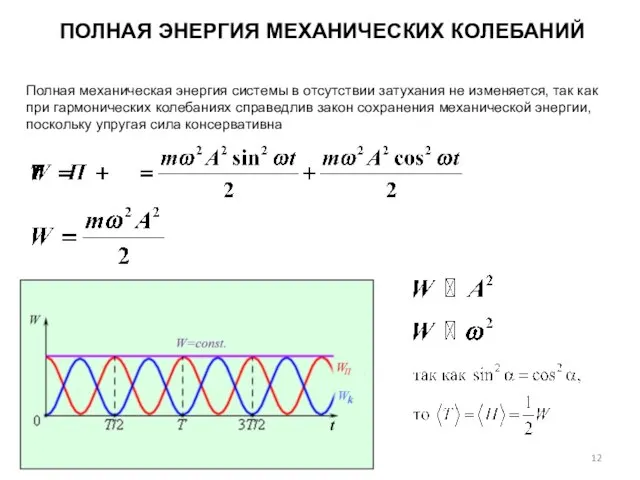
- 12. ПОЛНАЯ ЭНЕРГИЯ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ Полная механическая энергия системы в отсутствии затухания не изменяется, так как при
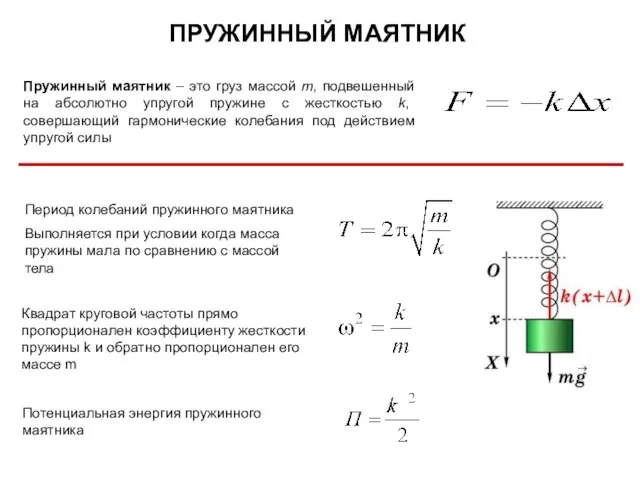
- 13. Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине с жесткостью k, совершающий
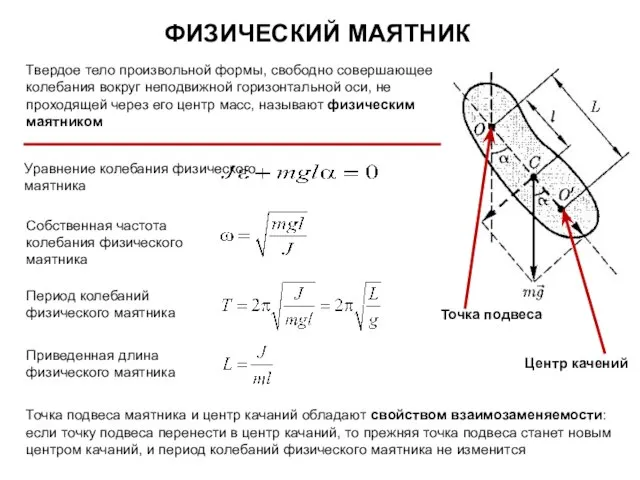
- 14. ФИЗИЧЕСКИЙ МАЯТНИК Твердое тело произвольной формы, свободно совершающее колебания вокруг неподвижной горизонтальной оси, не проходящей через
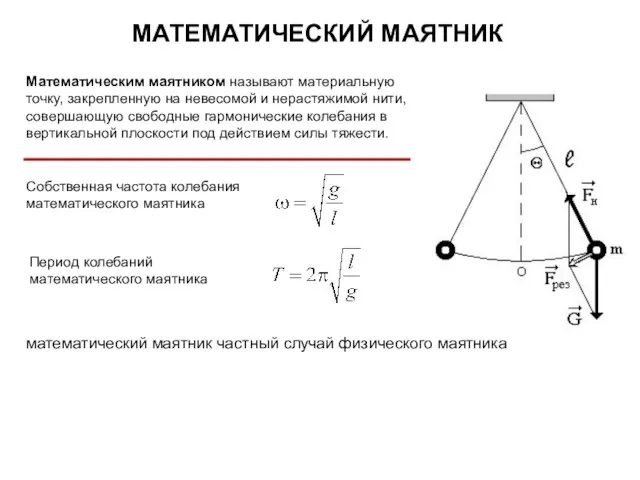
- 15. МАТЕМАТИЧЕСКИЙ МАЯТНИК Математическим маятником называют материальную точку, закрепленную на невесомой и нерастяжимой нити, совершающую свободные гармонические
- 16. БАЛЛИСТИЧЕСКИЙ МАЯТНИК Баллистический маятник представляет собой тяжелое тело, подвешенное на двойных нитях закон сохранения импульса закон
- 17. ЗАДАЧИ 1. Написать уравнение гармонического колебательного движения с амплитудой A = 5 см, если за время
- 18. ЗАДАЧИ 8. К пружине подвешен груз массой m = 10 кг. Зная, что пружина под влиянием
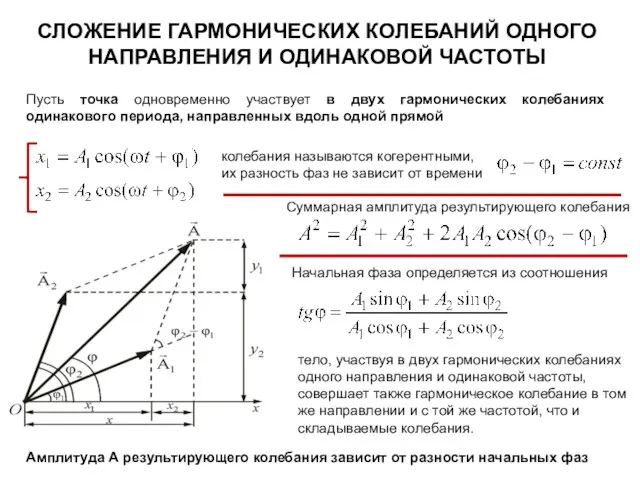
- 19. СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ ОДНОГО НАПРАВЛЕНИЯ И ОДИНАКОВОЙ ЧАСТОТЫ Пусть точка одновременно участвует в двух гармонических колебаниях
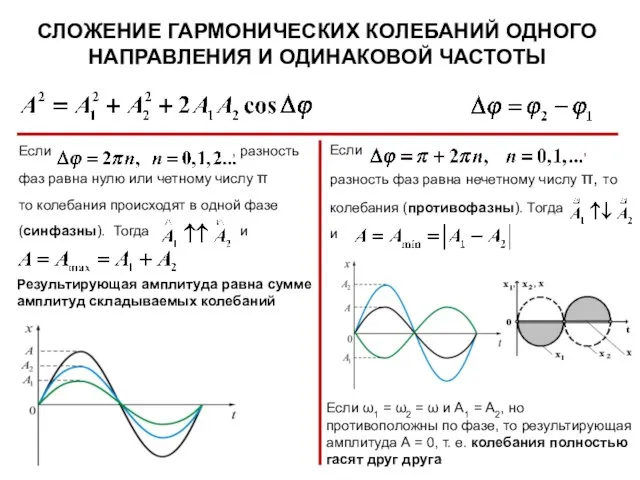
- 20. Если , разность фаз равна нулю или четному числу π то колебания происходят в одной фазе
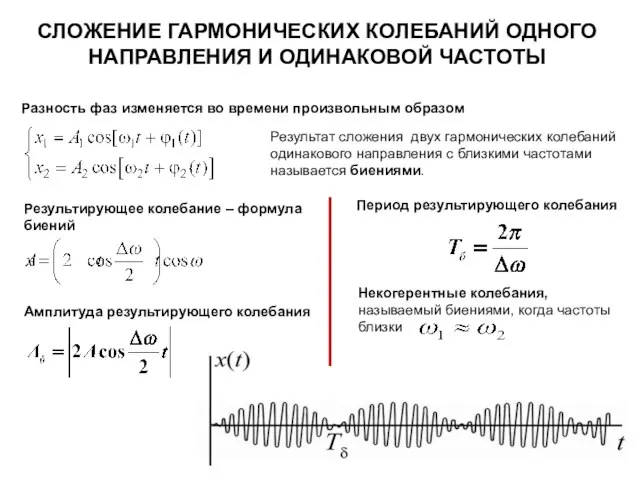
- 21. СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ ОДНОГО НАПРАВЛЕНИЯ И ОДИНАКОВОЙ ЧАСТОТЫ Разность фаз изменяется во времени произвольным образом Результат
- 22. СЛОЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ Уравнения двух взаимно перпендикулярных колебаний В результате получили уравнение эллипса с произвольно
- 23. уравнение прямой линии СЛОЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ уравнение эллипса уравнение эллипса уравнение прямой линии амплитуда колебаний
- 24. СЛОЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ Разность фаз складываемых взаимно перпендикулярных колебаний равна нечетному числу π/2, т. е.
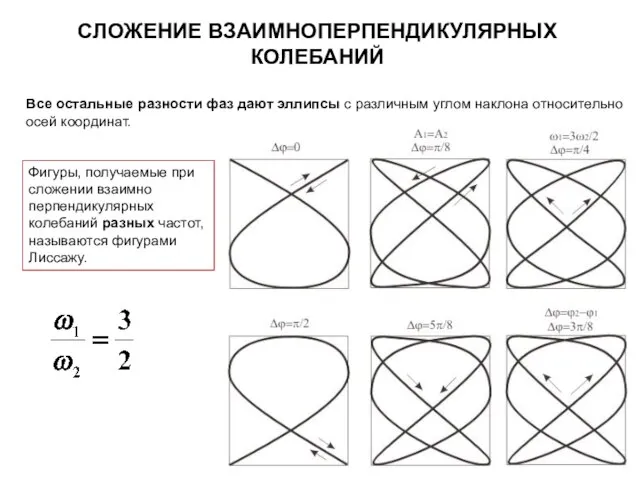
- 25. СЛОЖЕНИЕ ВЗАИМНОПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ Все остальные разности фаз дают эллипсы с различным углом наклона относительно осей координат.
- 26. 11. Написать уравнение движения, получающегося в результате сложения двух одинаково направленных гармонических колебательных, колебаний с одинаковым
- 27. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СВОБОДНЫХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ Затухающие колебания — колебания, амплитуды которых из-за потерь энергии с течением
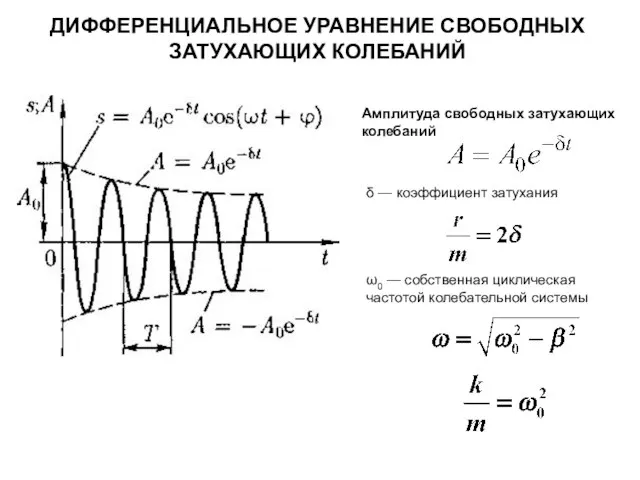
- 28. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СВОБОДНЫХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ Амплитуда свободных затухающих колебаний δ — коэффициент затухания ω0 — собственная
- 29. Промежуток времени τ = 1/δ, в течение которого амплитуда затухающих колебаний уменьшается в е = 2.7
- 30. Механические колебания, возникающие под действием внешней периодически изменяющейся силы называются вынужденными механическими колебаниями. Амплитуда вынужденных колебаний
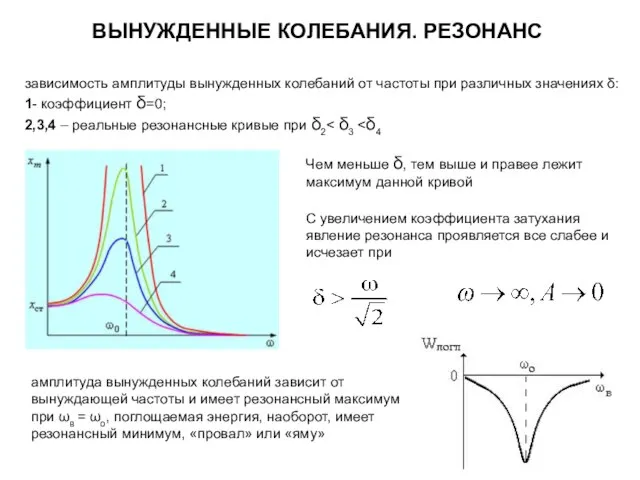
- 31. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС зависимость амплитуды вынужденных колебаний от частоты при различных значениях δ: 1- коэффициент δ=0;
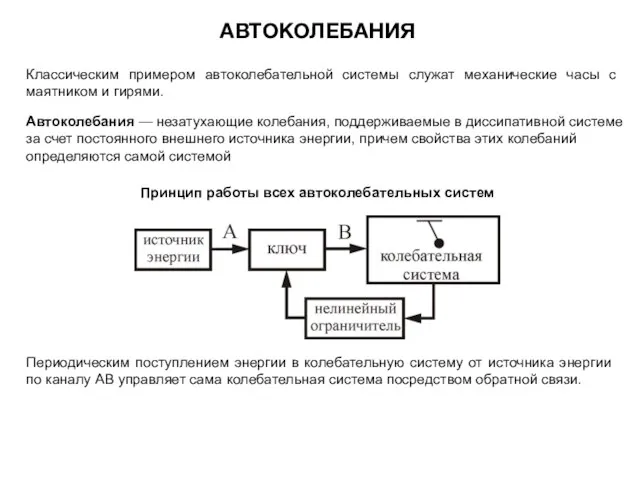
- 32. АВТОКОЛЕБАНИЯ Принцип работы всех автоколебательных систем Периодическим поступлением энергии в колебательную систему от источника энергии по
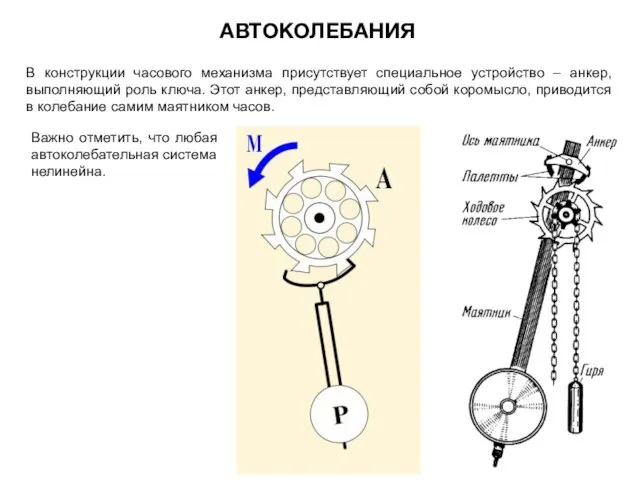
- 33. В конструкции часового механизма присутствует специальное устройство – анкер, выполняющий роль ключа. Этот анкер, представляющий собой
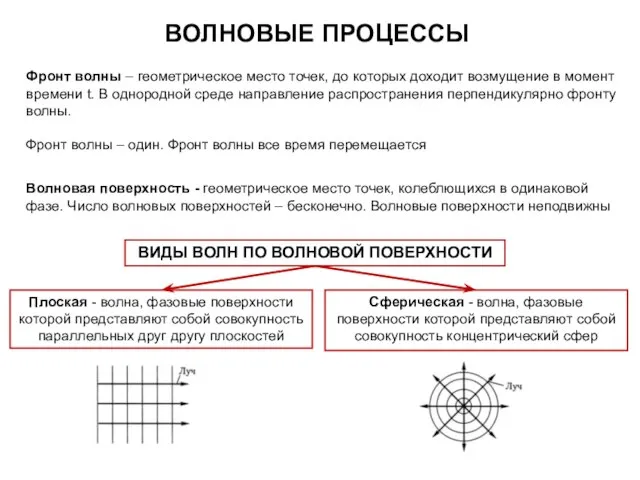
- 34. ВОЛНОВЫЕ ПРОЦЕССЫ При распространении волны, частицы среды не движутся вместе с волной, а колеблются около своих
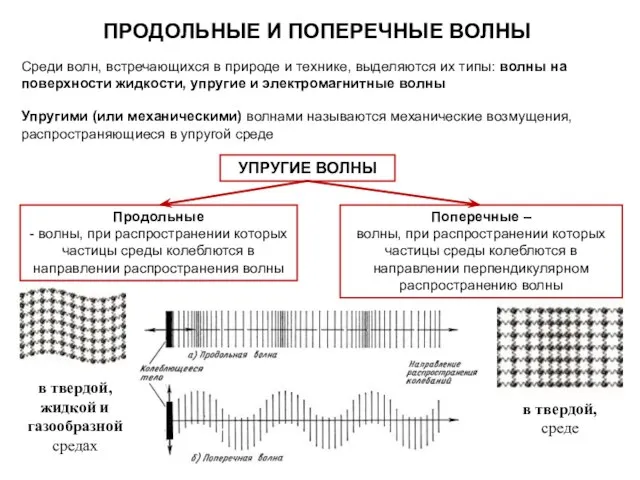
- 35. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ВОЛНЫ Среди волн, встречающихся в природе и технике, выделяются их типы: волны на
- 36. G - модуль сдвига ρ - плотность среды Поперечные волны связаны с упругими деформациями сдвига. Возможны
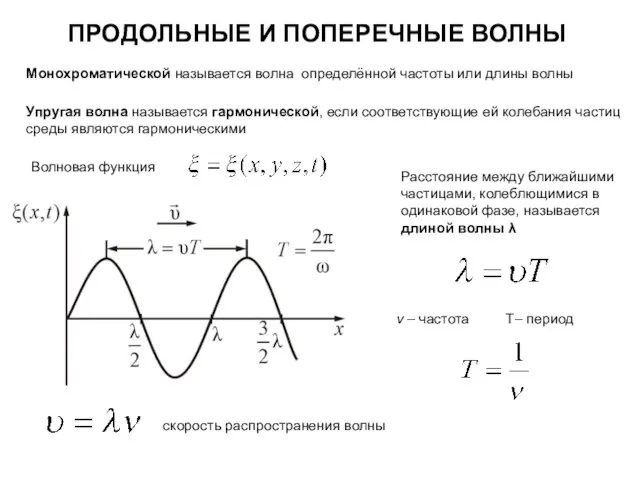
- 37. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ВОЛНЫ Монохроматической называется волна определённой частоты или длины волны Упругая волна называется гармонической,
- 38. ВОЛНОВЫЕ ПРОЦЕССЫ Фронт волны – геометрическое место точек, до которых доходит возмущение в момент времени t.
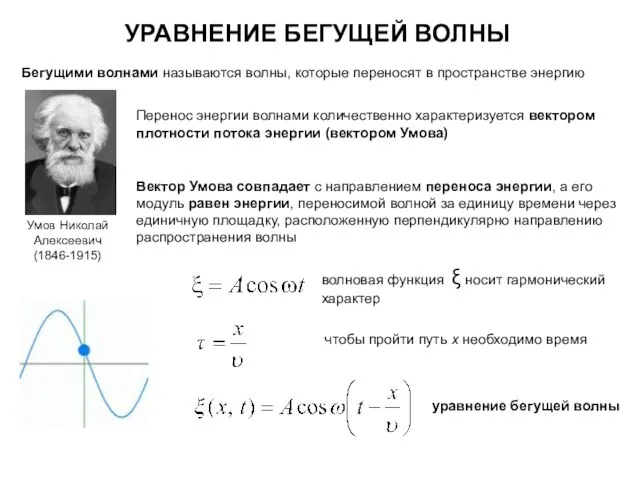
- 39. УРАВНЕНИЕ БЕГУЩЕЙ ВОЛНЫ Бегущими волнами называются волны, которые переносят в пространстве энергию Перенос энергии волнами количественно
- 40. Для характеристики волн используют волновое число Тогда уравнение плоской волны запишется так УРАВНЕНИЕ БЕГУЩЕЙ ВОЛНЫ Скорость
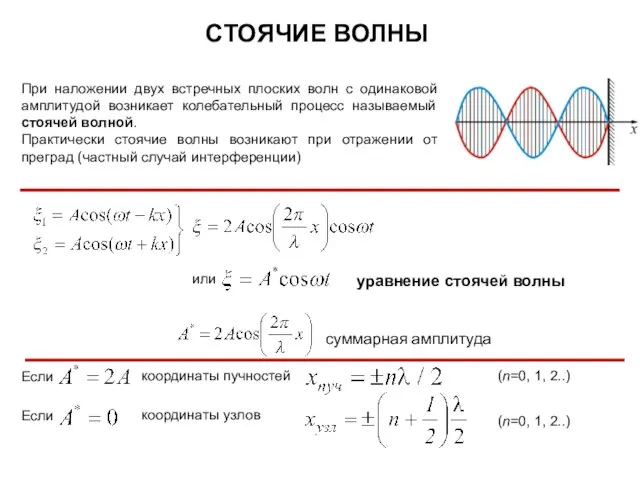
- 41. СТОЯЧИЕ ВОЛНЫ При наложении двух встречных плоских волн с одинаковой амплитудой возникает колебательный процесс называемый стоячей
- 43. Скачать презентацию

















 Волноводы с волнами типа Т. Лекция 11
Волноводы с волнами типа Т. Лекция 11 Гидрогазодинамика. Элементы теории гидродинамического пограничного слоя. (Тема 1. Лекции 3,4)
Гидрогазодинамика. Элементы теории гидродинамического пограничного слоя. (Тема 1. Лекции 3,4) Ядерное оружие
Ядерное оружие Получение и применение кристаллов
Получение и применение кристаллов  I.Механика. Кинематика
I.Механика. Кинематика 1. ОСНОВНЫЕ СВЕТОТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ 2. ВИДЫ ОСВЕЩЕНИЯ 3. НОРМИРОВАНИЕ 4. ИСТОЧНИКИ СВЕТА И СВЕТИЛЬНИКИ
1. ОСНОВНЫЕ СВЕТОТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ 2. ВИДЫ ОСВЕЩЕНИЯ 3. НОРМИРОВАНИЕ 4. ИСТОЧНИКИ СВЕТА И СВЕТИЛЬНИКИ Презентация по физике "Конвекция в природе и технике" - скачать
Презентация по физике "Конвекция в природе и технике" - скачать  ВЛАЖНОСТЬ ВОЗДУХА. Работу выполнила Ученица 9 «В» класса МОУ Лицея № 1 Сермягина Анастасия.
ВЛАЖНОСТЬ ВОЗДУХА. Работу выполнила Ученица 9 «В» класса МОУ Лицея № 1 Сермягина Анастасия. Поверхностное натяжение жидкости. Смачивание. Капиллярность
Поверхностное натяжение жидкости. Смачивание. Капиллярность Электричество и магнетизм. Лекция 14. Индуктивность. Цепи переменного тока. Энергия электро-магнитного поля
Электричество и магнетизм. Лекция 14. Индуктивность. Цепи переменного тока. Энергия электро-магнитного поля Элементы линейной алгебры в электротехнике (электронное учебное пособие)
Элементы линейной алгебры в электротехнике (электронное учебное пособие) Поисково-исследовательский метод используемый на уроках физики
Поисково-исследовательский метод используемый на уроках физики Моделирование электростатического поля
Моделирование электростатического поля Напряженно-деформированное состояние
Напряженно-деформированное состояние Магнитные свойства материалов
Магнитные свойства материалов Производство, передача и потребление электроэнергии. Типы электростанций
Производство, передача и потребление электроэнергии. Типы электростанций Электростатика
Электростатика Тематический тест по физике для текущего контроля
Тематический тест по физике для текущего контроля Энергия. Работа. Законы сохранения
Энергия. Работа. Законы сохранения Второй закон Ньютона
Второй закон Ньютона Электромагнит и его применение
Электромагнит и его применение Электр құбылыстары
Электр құбылыстары Презентация по физике "Жидкие кристаллы" - скачать
Презентация по физике "Жидкие кристаллы" - скачать  Термоэлектрические явления в металлах и полупроводниках
Термоэлектрические явления в металлах и полупроводниках Презентация Простые механизмы
Презентация Простые механизмы  Испарение и конденсация. Насыщенные и ненасыщенные пары. Влажность воздуха
Испарение и конденсация. Насыщенные и ненасыщенные пары. Влажность воздуха Глава IV. Векторы в пространстве
Глава IV. Векторы в пространстве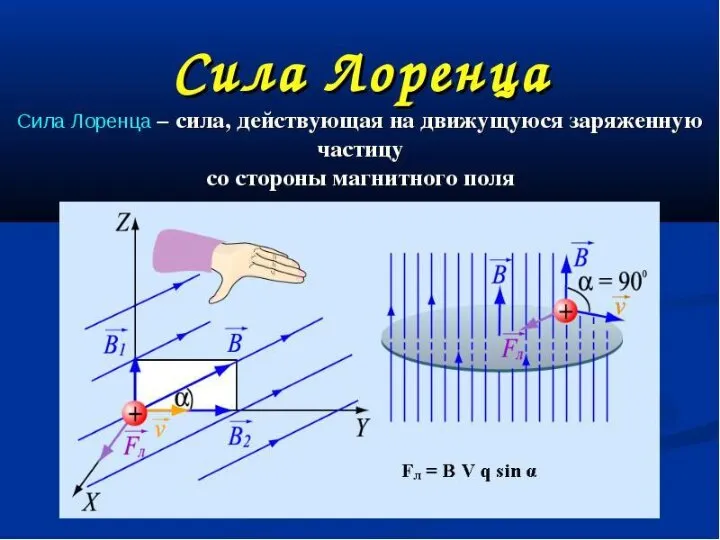 Сила Лоренца. Модуль силы Лоренца
Сила Лоренца. Модуль силы Лоренца