Содержание
- 2. Актуальность Волна – это потенциальное опасное явление для плавающих и закрепленных на воде сооружений.
- 3. Цель Создание численной модели работы волнопродуктора поршневого типа комплексным методом граничных элементов и определения диапазона скоростей
- 4. Задачи Реализация КМГЭ Тестирование методом пробных функций Реализация алгоритма движения по времени Реализация алгоритма вычисления поля
- 5. Постановка задачи Дана область течения D, ограниченная твердыми стенками, свободной границей и твердой перемещающейся стенкой. На
- 6. На свободной границе выполняются кинематическое и динамическое условия: (3) (4) На торцевой стенке поршня задано следующее
- 7. Алгоритм решения Краевая задача (1)-(5) в которой время явно входит только в (3) и (4). Данные
- 8. Для определения положения свободной границы и вычисления потенциала на ней в определенный момент времени находятся по
- 9. После получения новой смешанной краевой задачи с условиями (2), (5) и (7) необходимо определить значение функции
- 10. для точки на границе С, для внутренней точки , а для угловой точки . Обход области
- 11. После разбиения и линейной аппроксимации функции w(z) на границе интеграл Коши можно вычислить аналитически в смысле
- 12. После нахождения значения функций тока и потенциала скорости на всей границе D требуется вычислить компоненты скорости
- 14. Скачать презентацию











 Электромагнитная природа света. Интерференция света
Электромагнитная природа света. Интерференция света Физика и техника
Физика и техника Виды физических явлений. Тела и вещества
Виды физических явлений. Тела и вещества Механическая работа. Единицы работы
Механическая работа. Единицы работы Научный раздел
Научный раздел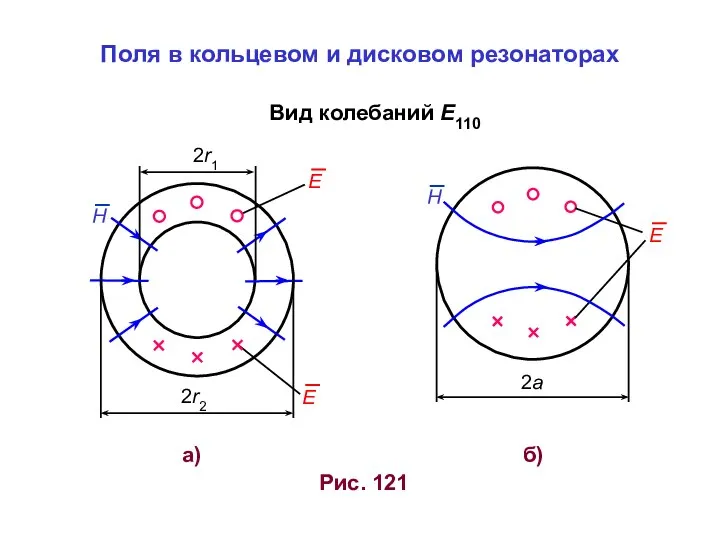 Поля в кольцевом и дисковом резонаторах
Поля в кольцевом и дисковом резонаторах Режим біжучої хвилі при ZH=RH=ZХ. (Лекция 14)
Режим біжучої хвилі при ZH=RH=ZХ. (Лекция 14) Электрохимиялық генератор
Электрохимиялық генератор Векторлар өрісі және оның сипаттамалары
Векторлар өрісі және оның сипаттамалары Рабочие процессы дизельного двигателя
Рабочие процессы дизельного двигателя Уақыт тоқтатылуына тәуелсіз электрберіліс желісінің максималды қорғанысы
Уақыт тоқтатылуына тәуелсіз электрберіліс желісінің максималды қорғанысы Ядерный взрыв и его опасные факторы
Ядерный взрыв и его опасные факторы Термодинамика негіздері
Термодинамика негіздері Автономная система получения пресной воды
Автономная система получения пресной воды Феромагнітні рідини
Феромагнітні рідини Экспериментальные методы морской гидромеханики
Экспериментальные методы морской гидромеханики Курс «Основы вакуумной техники» Раздел «Экскурс в историю вакуумной техники: от эфира и технического вакуума до физического ваку
Курс «Основы вакуумной техники» Раздел «Экскурс в историю вакуумной техники: от эфира и технического вакуума до физического ваку Законы Ньютона
Законы Ньютона Теоретичские основы теплотехники
Теоретичские основы теплотехники Стабилитрон тақырыбына арналған презентация
Стабилитрон тақырыбына арналған презентация Презентация по физике "Силы в природе" - скачать
Презентация по физике "Силы в природе" - скачать  Презентация по физике "Электрическое сопротивление проводника. Удельное сопротивление" - скачать
Презентация по физике "Электрическое сопротивление проводника. Удельное сопротивление" - скачать  Спектроскопия
Спектроскопия Закон всемирного тяготения
Закон всемирного тяготения Теплопроводность
Теплопроводность Кинематика. (Лекция 2)
Кинематика. (Лекция 2) Вопросы ИК-спектроскопии органических соединений
Вопросы ИК-спектроскопии органических соединений Действия электрического тока
Действия электрического тока