Содержание
- 2. Синхронизация автоколебаний – одно из фундаментальных явлений природы Автоколебательная система (АК) период T (для периодических АК);
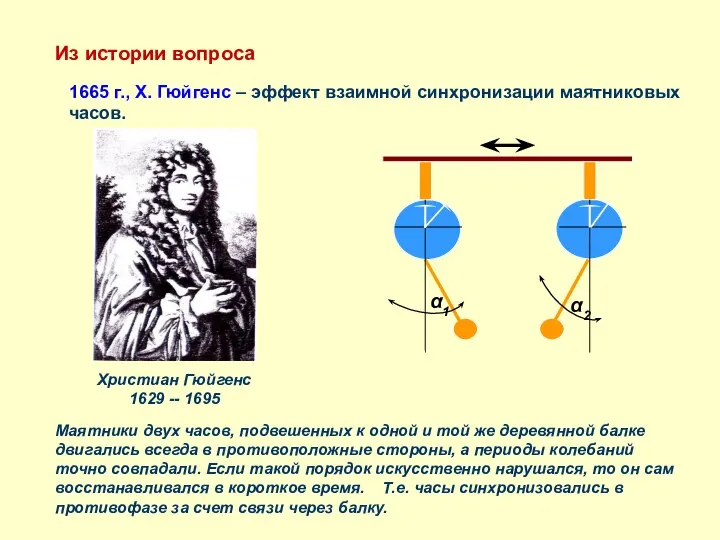
- 3. Из истории вопроса 1665 г., Х. Гюйгенс – эффект взаимной синхронизации маятниковых часов. Маятники двух часов,
- 4. Середина XIX в., лорд Дж. Рэлей – синхронизация в акустических системах. Рэлей наблюдал взаимную синхронизацию двух
- 5. 1930 г., А. А. Андронов, А. А, Витт -- создана законченная теория синхронизации автогенератора внешним гармоническим
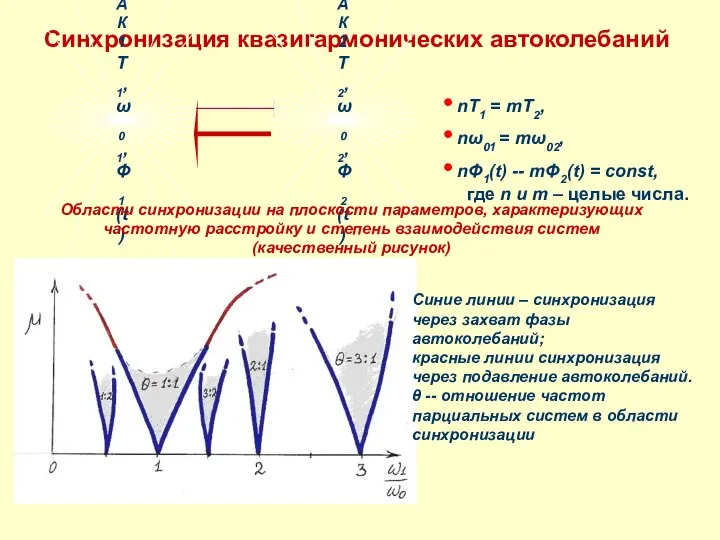
- 6. Синхронизация квазигармонических автоколебаний nT1 = mT2, nω01 = mω02, nΦ1(t) -- mΦ2(t) = const, где n
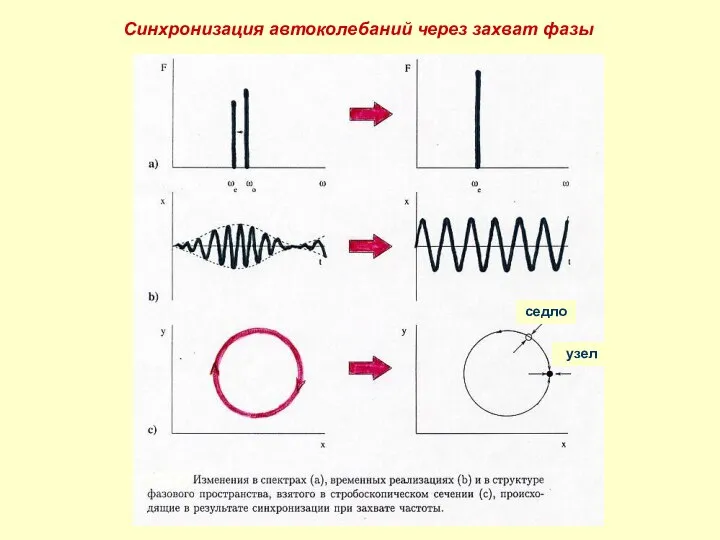
- 7. Синхронизация автоколебаний через захват фазы седло узел
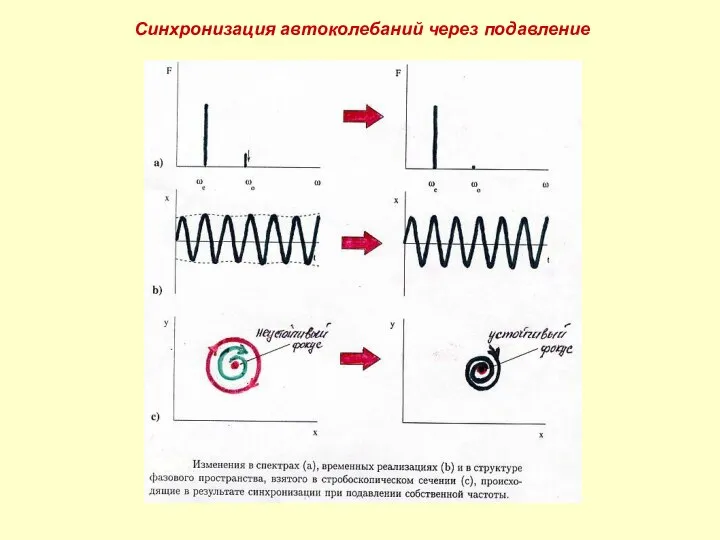
- 8. Синхронизация автоколебаний через подавление
- 9. Вынужденная синхронизация автогенератора. Классическая теория Модель -- генератор Ван дер Поля с внешним гармоническим воздействием: a
- 10. где μ = a/2ω1, Δ = ω0 -ω1 – расстройка частот, A0 – невозмущенная амплитуда. Состояния
- 11. Фазовое приближение Считаем, что амплитуда воздействия a мала. Тогда A( t )≈ A0 и можно записать
- 12. Область существования состояний равновесия уравнения (4) определяется условием | Δ | В этой области в системе
- 13. Мгновенная частота биений есть периодическая функция с периодом Средняя частота биений характеризует расстройку частоты автоколебаний и
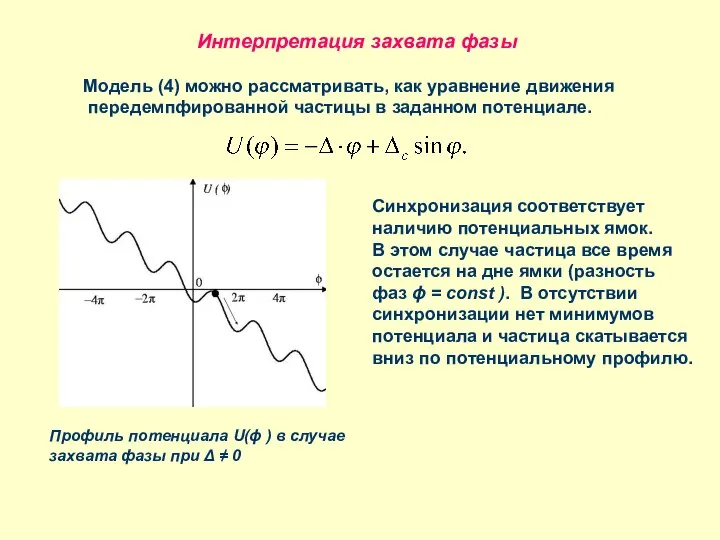
- 14. Интерпретация захвата фазы Модель (4) можно рассматривать, как уравнение движения передемпфированной частицы в заданном потенциале. Профиль
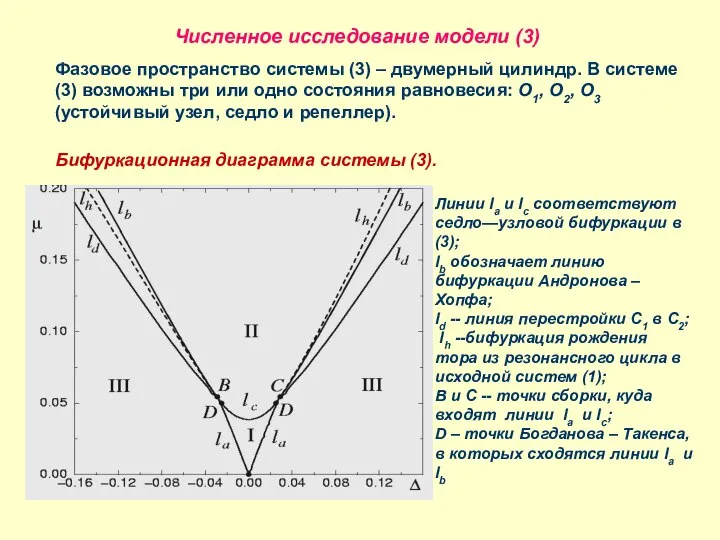
- 15. Численное исследование модели (3) Фазовое пространство системы (3) – двумерный цилиндр. В системе (3) возможны три
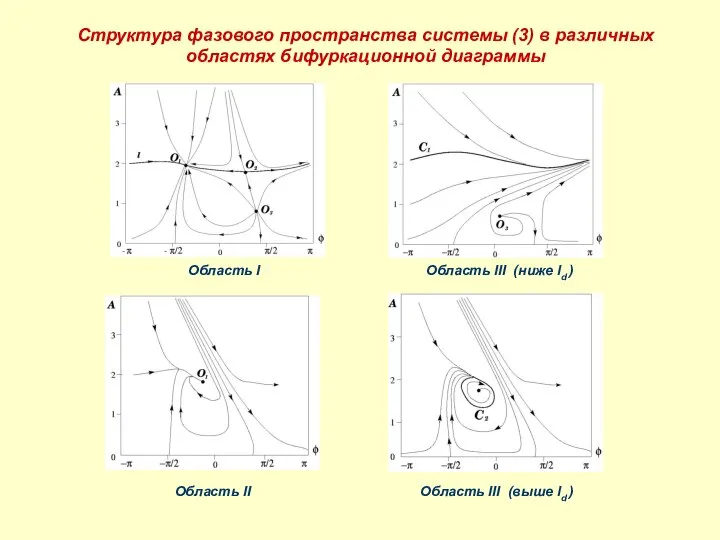
- 16. Структура фазового пространства системы (3) в различных областях бифуркационной диаграммы Область I Область II Область III
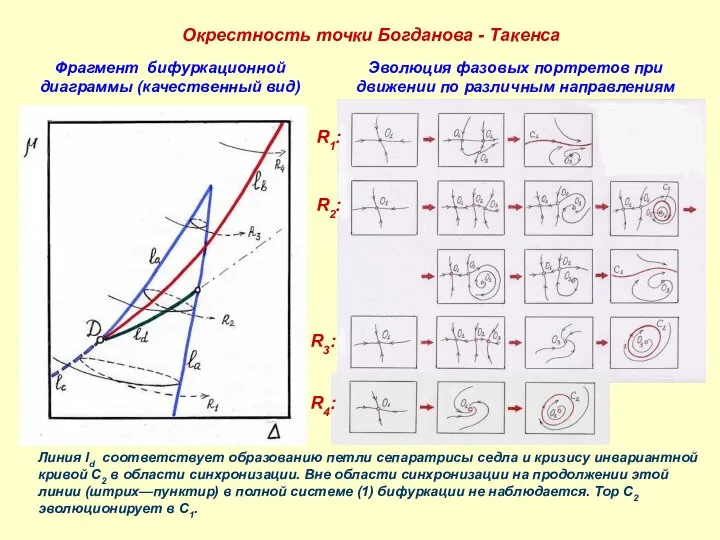
- 17. Окрестность точки Богданова - Такенса Фрагмент бифуркационной диаграммы (качественный вид) Эволюция фазовых портретов при движении по
- 18. Синхронизация в присутствии шума В реальных системах всегда присутствует шум (внутренний шум и случайные воздействия со
- 19. Модель -- генератор Ван дер Поля с внешним гармоническим воздействием и источником шума: где ξ (
- 20. Стохастические укороченные уравнения для амплитуды A( t ) и фазы ϕ ( t ) имеют вид:
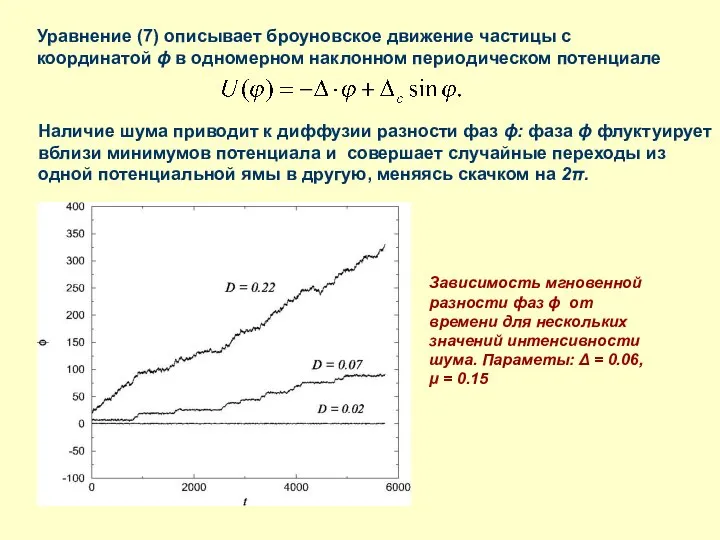
- 21. Уравнение (7) описывает броуновское движение частицы с координатой ϕ в одномерном наклонном периодическом потенциале Наличие шума
- 22. Увеличение интенсивности шума приводит к уменьшению длительности пребывания ϕ одной потенциальной ямке. Частица быстрее скатывается по
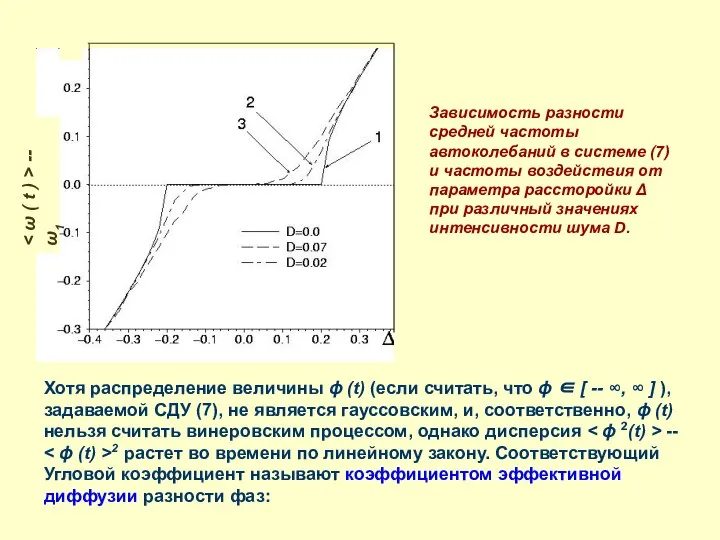
- 23. -- ω1 Зависимость разности средней частоты автоколебаний в системе (7) и частоты воздействия от параметра рассторойки
- 24. Величина Deff характеризует среднее число сбоев разности фаз на 2π в единицу времени. Она возрастает с
- 26. Скачать презентацию













 Навчальний проект: «Ця важка робота»
Навчальний проект: «Ця важка робота» Циклотрон
Циклотрон Выбор допускаемых напряжений. (Лекция 3)
Выбор допускаемых напряжений. (Лекция 3) Разработка системы управления узлом подготовки реакционной смеси с применением САР соотношения расходов
Разработка системы управления узлом подготовки реакционной смеси с применением САР соотношения расходов Siltumfizikas pamati. Enerģijas mērvienības, spiediens, degšana, siltumapmaiņa, tvaika veidošanās
Siltumfizikas pamati. Enerģijas mērvienības, spiediens, degšana, siltumapmaiņa, tvaika veidošanās Электрические свойства кристаллов
Электрические свойства кристаллов Интеллектуальная игра «Физбой»
Интеллектуальная игра «Физбой»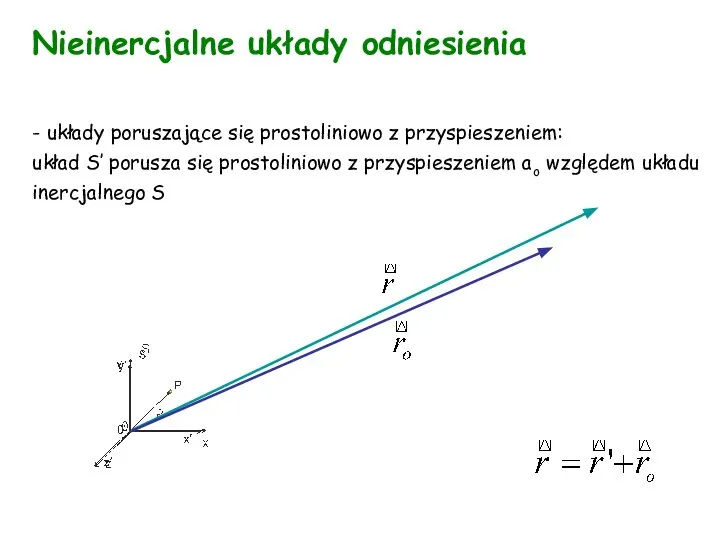 Nieinercjalne układy odniesienia
Nieinercjalne układy odniesienia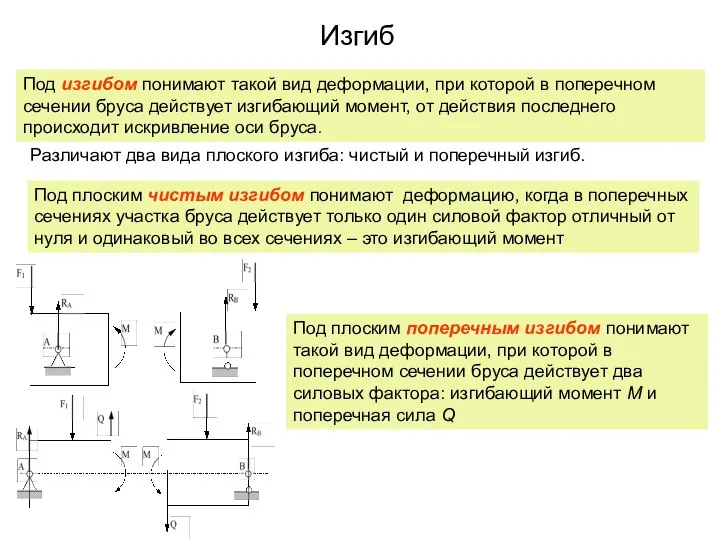 Изгиб
Изгиб Comissioning of Upgraded VEPP-2000. Injection Chain
Comissioning of Upgraded VEPP-2000. Injection Chain Вращательное движение твёрдого тела
Вращательное движение твёрдого тела Урок физики в 7 кл. Тема: Сложение двух сил, направленных по одной прямой. Равнодействующая сил.
Урок физики в 7 кл. Тема: Сложение двух сил, направленных по одной прямой. Равнодействующая сил. Архимедова сила
Архимедова сила Магнитное поле катушки с током. Электромагнит
Магнитное поле катушки с током. Электромагнит Обеспечение повышения качества поверхности и эксплуатационных свойств деталей машин, работающих при статическом нагружении
Обеспечение повышения качества поверхности и эксплуатационных свойств деталей машин, работающих при статическом нагружении Сложение потенциальных потоков
Сложение потенциальных потоков Электростатическое поле. Лекция 1а
Электростатическое поле. Лекция 1а Энергияның дәстүрден тыс коздері. Күн энергиясы немесе гелиоэнергетика
Энергияның дәстүрден тыс коздері. Күн энергиясы немесе гелиоэнергетика Классификация способов обработки материалов потоками излучения
Классификация способов обработки материалов потоками излучения Понятие о радиоволнах. Деление волн на диапазоны. Основные физические свойства радиоволн. Распространение радиоволн
Понятие о радиоволнах. Деление волн на диапазоны. Основные физические свойства радиоволн. Распространение радиоволн Понятие и определение статики
Понятие и определение статики Ядерная физика
Ядерная физика Отсчёт по практике. Электричество
Отсчёт по практике. Электричество Равномерное движение по окружности
Равномерное движение по окружности Инерция. Билет 2
Инерция. Билет 2 Бесцентровое шлифование наружных поверхностей тел вращения
Бесцентровое шлифование наружных поверхностей тел вращения Механические и электромагнитные колебания. Лекция 24
Механические и электромагнитные колебания. Лекция 24 Электрические контакты и условия работы
Электрические контакты и условия работы