Содержание
- 2. Явление синхронизации наблюдается не только в автоколебательных системах с регулярной динамикой, но и в системах, находящихся
- 3. Классический подход к проблеме синхронизации хаотических автоколебаний. Частотно – фазовая синхронизация Классические представления о синхронизации можно
- 4. используя последовательность моментов времени tk, соответствующих пересечению траекторией некоторой секущей плоскости в одном направлении (3) В
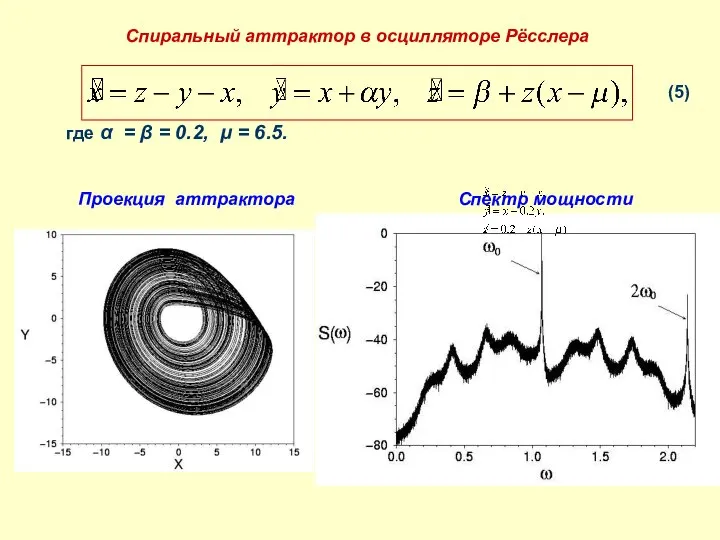
- 5. Спиральный аттрактор в осцилляторе Рёсслера где α = β = 0.2, μ = 6.5. Проекция аттрактора
- 6. Частотно – фазовая синхронизация хаоса означает: Кратность базовых часто взаимодействующих систем nω01 = mω02; Ограниченность разности
- 7. Численное исследование частотно –фазовой синхронизации хаоса в системе Рёсслера с гармоническим внешним воздействием Модель: α =
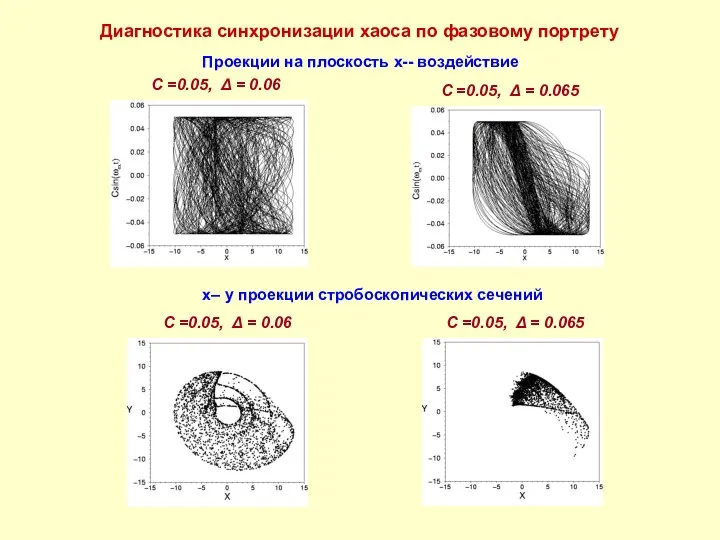
- 8. Диагностика синхронизации хаоса по фазовому портрету Проекции на плоскость x-- воздействие C =0.05, Δ = 0.06
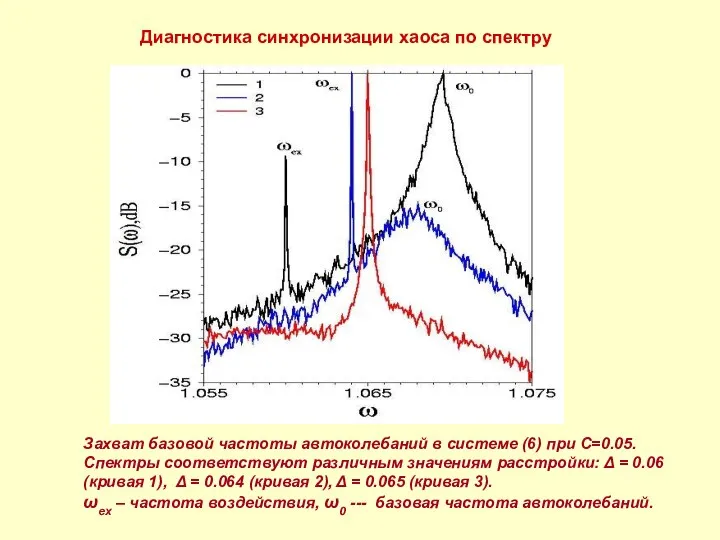
- 9. Диагностика синхронизации хаоса по спектру Захват базовой частоты автоколебаний в системе (6) при C=0.05. Спектры соответствуют
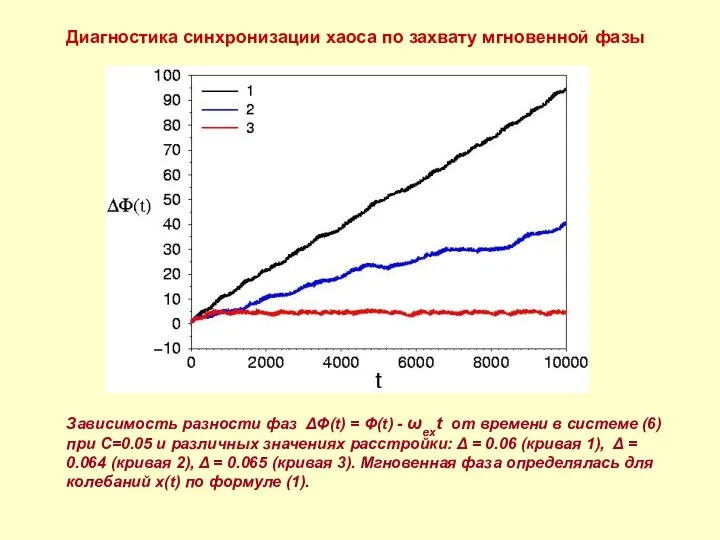
- 10. Диагностика синхронизации хаоса по захвату мгновенной фазы Зависимость разности фаз ΔΦ(t) = Φ(t) - ωext от
- 11. Диагностика области синхронизации в системе (6) Зависимость числа вращения Θ от частоты воздействия в системе (6)
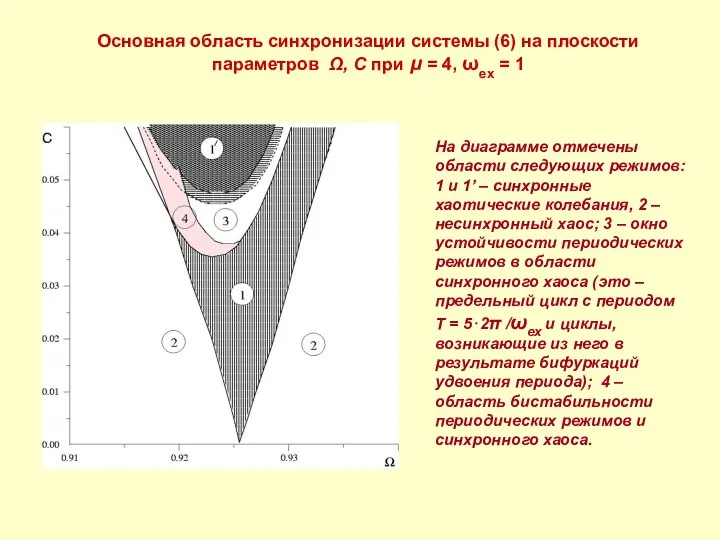
- 12. Основная область синхронизации системы (6) на плоскости параметров Ω, C при μ = 4, ωex =
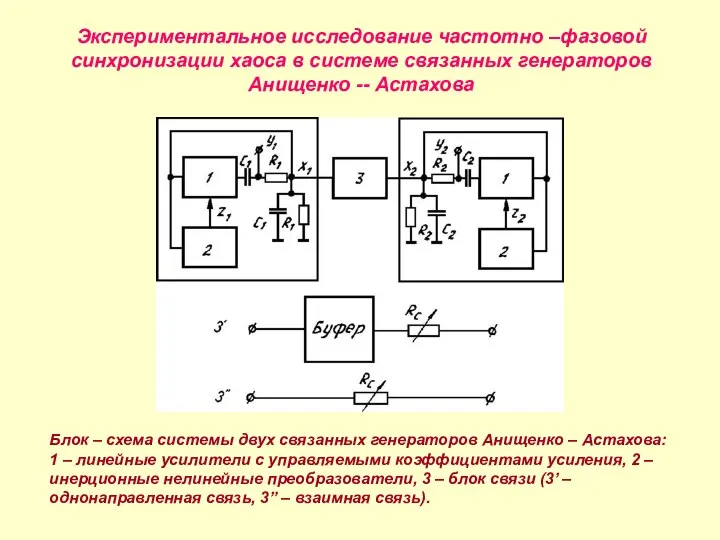
- 13. Экспериментальное исследование частотно –фазовой синхронизации хаоса в системе связанных генераторов Анищенко -- Астахова Блок – схема
- 14. Математическая модель экспериментальной системы (6) где m12 и g12 – параметры, управляющие динамическим режимом парциального генератора;
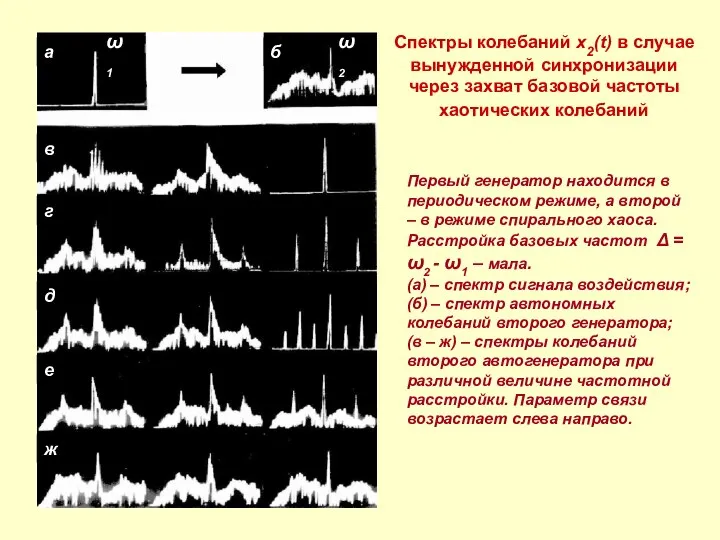
- 15. Спектры колебаний x2(t) в случае вынужденной синхронизации через захват базовой частоты хаотических колебаний Первый генератор находится
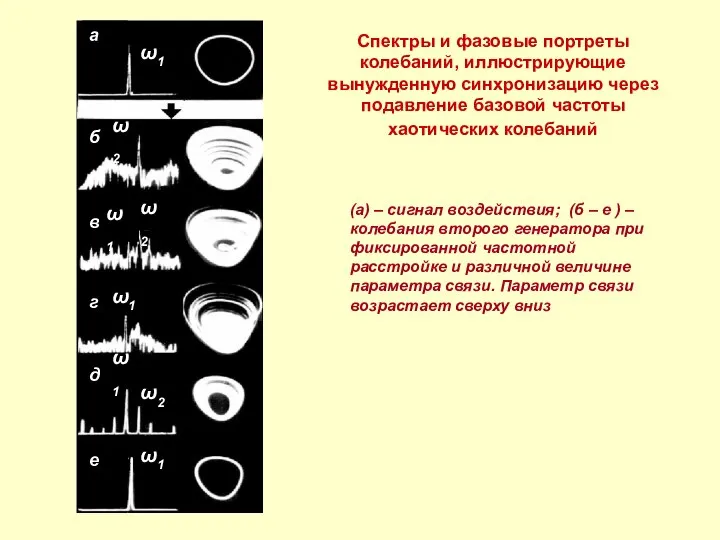
- 16. Спектры и фазовые портреты колебаний, иллюстрирующие вынужденную синхронизацию через подавление базовой частоты хаотических колебаний (а) –
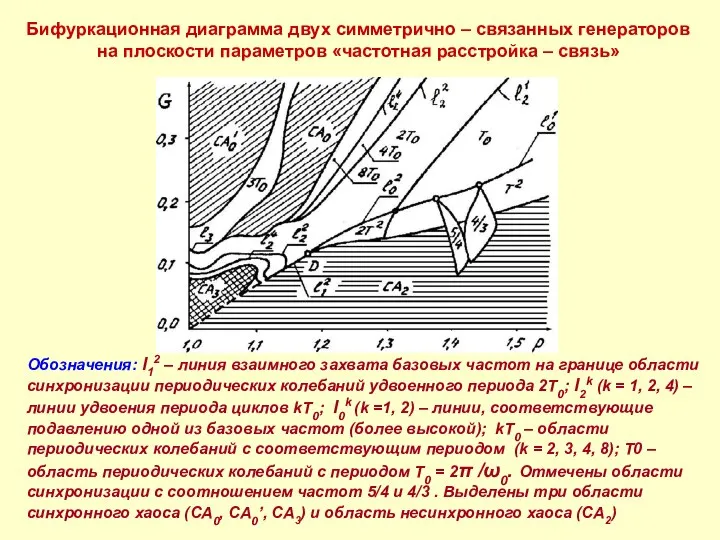
- 17. Бифуркационная диаграмма двух симметрично – связанных генераторов на плоскости параметров «частотная расстройка – связь» Обозначения: l12
- 18. Полная синхронизация взаимодействующих хаотических систем При взаимодействии (в том числе однонаправленном) двух совершенно идентичных хаотических систем
- 19. Если предельное множество, принадлежащее U, притягивает фазовые траектории не только из U, но и из некоторой
- 20. Проекции аттракторов в системе (8) в режиме полной синхронизации при α = β = 0.2, μ
- 21. Замечания. Полная синхронизация может наблюдаться не только в режиме спирального хаоса, но и в более сложных
- 23. Скачать презентацию











 Введение в электротехнику
Введение в электротехнику Основы вакуумной техники
Основы вакуумной техники Магнетизм. Магнитостатика. Магнитное взаимодействие
Магнетизм. Магнитостатика. Магнитное взаимодействие Презентация по физике "Колебательный контур" - скачать
Презентация по физике "Колебательный контур" - скачать  Електричне поле
Електричне поле Линии передачи электромагнитных волн. Проволочные и кабельные линии передачи радиоволн. (Тема 1.2)
Линии передачи электромагнитных волн. Проволочные и кабельные линии передачи радиоволн. (Тема 1.2) Работа силы. Мощность
Работа силы. Мощность Трансформатор Тесла
Трансформатор Тесла Теория подобия и моделирования
Теория подобия и моделирования Сложное движение точки
Сложное движение точки Развитие средств связи
Развитие средств связи Электромагнитное взаимодействие
Электромагнитное взаимодействие Инженерные расчеты численными методами
Инженерные расчеты численными методами Презентация Реактивное движение
Презентация Реактивное движение  Шинные конструкции
Шинные конструкции Лекция №12 Электрический ток План лекции 1. Понятие о токе проводимости. Вектор тока и сила тока. 2. Дифференциальная форма закона О
Лекция №12 Электрический ток План лекции 1. Понятие о токе проводимости. Вектор тока и сила тока. 2. Дифференциальная форма закона О Элементы специальной теории относительности (СТО). Релятивистская динамика
Элементы специальной теории относительности (СТО). Релятивистская динамика Электрический ток в различных средах. Электрический ток в металлах
Электрический ток в различных средах. Электрический ток в металлах Электрическое поле в веществе
Электрическое поле в веществе Системы управления трактором
Системы управления трактором Основы расчета и безопасной эксплуатации элементов, моделируемых в форме тонкостенной оболочки
Основы расчета и безопасной эксплуатации элементов, моделируемых в форме тонкостенной оболочки Резонанс. Полезный резонанс
Резонанс. Полезный резонанс Динамическое проектирование систем стабилизации летательных аппаратов. Исполнительные устройства. Энергетический расчет
Динамическое проектирование систем стабилизации летательных аппаратов. Исполнительные устройства. Энергетический расчет Охлаждение, нагревание тел конечных размеров. Нагрев параллелепипеда
Охлаждение, нагревание тел конечных размеров. Нагрев параллелепипеда Волоконно - оптические элементы
Волоконно - оптические элементы Государственная система обеспечения единства измерений. Единицы величин
Государственная система обеспечения единства измерений. Единицы величин Система мониторинга водного баланса Балтийского моря
Система мониторинга водного баланса Балтийского моря Основы хроматографического анализа
Основы хроматографического анализа