Содержание
■ Теорема о сложении ускорений (теорема Кориолиса) – абсолютное ускорение точки
■ Теорема о сложении ускорений (теорема Кориолиса) – абсолютное ускорение точки
переносного и кориолисова ускорений точки.
Было получено ранее соотношение для скорости:
Продифференцируем это соотношение
по времени еще раз:
Здесь первое слагаемое (aO) - ускорение полюса O;
следующие три – относительное ускорение точки (ar).
Для последних трех слагаемых
следует определить вторые производные по времени
от ортов подвижной системы
координат i, j, k:
Подставим эти выражения
в последние три слагаемые
и сгруппируем:
Сумма первого и полученных
двух слагаемых – ускорение
точки свободного тела есть
переносное
ускорение точки (ae):
В оставшихся шести слагаемых сложим одинаковые члены, подставим векторные произведения для первых производных по времени от ортов и сгруппируем:
Полученная компонента ускорения представляет собой кориолисово ускорение (ac):
Таким образом, с учетом того, что вторая производная по времени
радиуса-вектора ρ есть абсолютное ускорение, получаем:
■ Величина и направление ускорения Кориолиса:
Модуль вектора кориолисова ускорения:
Ускорение Кориолиса обращается в ноль
в двух случаях:
Угловая скорость переносного движения равна 0 (поступательное
переносное движение).
Вектор угловой скорости параллелен вектору относительной
скорости (синус угла между векторами обращается в 0).
Направление вектора
кориолисова ускорения:
Определяется по одному
из трех правил:
По определению векторного
произведения (см. л.3.2).
По правилу правой руки (см. л.3.2).
По правилу Жуковского:
Спроецировать вектор относительной скорости
на плоскость, перпендикулярную вектору угловой скорости.
б) Повернуть проекцию вектора относительной скорости
на прямой угол в сторону дуговой стрелки угловой скорости.

 Поступательное и вращательное движения
Поступательное и вращательное движения МОУ «Основная общеобразовательная школа №9» Электромагнитное излучение Рентгеновские излучения Выполнил : ученик 8 класса Ники
МОУ «Основная общеобразовательная школа №9» Электромагнитное излучение Рентгеновские излучения Выполнил : ученик 8 класса Ники 15 минут о спектроскопии
15 минут о спектроскопии Капиллярная хроматография
Капиллярная хроматография Презентация по физике "Возобновляемые источники энергии" - скачать
Презентация по физике "Возобновляемые источники энергии" - скачать  Естественная радиоактивность Виды радиоактивных излучений
Естественная радиоактивность Виды радиоактивных излучений  Классификация сил, действующих на элементы конструкций
Классификация сил, действующих на элементы конструкций Механічна робота і потужність (7 клас)
Механічна робота і потужність (7 клас) Физические основы защиты информации от утечки по каналам побочных электромагнитных излучений и наводок
Физические основы защиты информации от утечки по каналам побочных электромагнитных излучений и наводок Системы автоматического управления (САУ). Теория автоматического управления (ТАУ)
Системы автоматического управления (САУ). Теория автоматического управления (ТАУ) Затухающие колебания
Затухающие колебания Сравнение количеств теплоты при смешивании воды разной температуры. Лабораторная работа №1
Сравнение количеств теплоты при смешивании воды разной температуры. Лабораторная работа №1 Прямолинейное равноускоренное движение - ПРУД
Прямолинейное равноускоренное движение - ПРУД Гипотеза де Бройля. Дифракция электронов. Микрочастица в двухщелевом интерферометре. Соотношение неопределенностей Гейзенберга
Гипотеза де Бройля. Дифракция электронов. Микрочастица в двухщелевом интерферометре. Соотношение неопределенностей Гейзенберга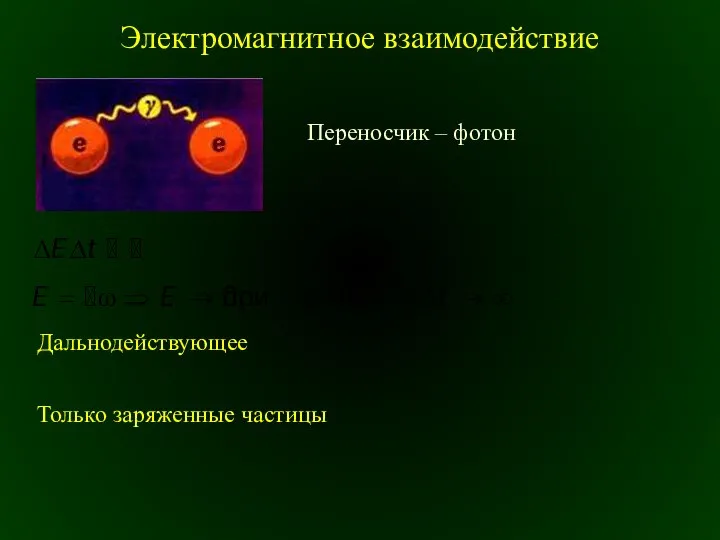 Электромагнитное взаимодействие
Электромагнитное взаимодействие Учитель физики МОУ «СОШ с. Агафоновка Питерского района Саратовской области» Дзюрич Елена Алексеевна
Учитель физики МОУ «СОШ с. Агафоновка Питерского района Саратовской области» Дзюрич Елена Алексеевна Аттестационная работа. Проектная деятельность на уроках физики
Аттестационная работа. Проектная деятельность на уроках физики Корпускулярно-волновой дуализм света
Корпускулярно-волновой дуализм света Основы физики наноструктур
Основы физики наноструктур Закон всемирного тяготения. Исаак Ньютон
Закон всемирного тяготения. Исаак Ньютон Распределения Бозе-Эйнштейна и Ферми-Дирака. Фазовое пространство. Плотность распределения. Лекция 19
Распределения Бозе-Эйнштейна и Ферми-Дирака. Фазовое пространство. Плотность распределения. Лекция 19 Основы теории антенн. Лекция № 6. АФУ
Основы теории антенн. Лекция № 6. АФУ Уравнение переноса излучения с учетом поглощения в линиях. (Тема 13)
Уравнение переноса излучения с учетом поглощения в линиях. (Тема 13) Материальная точка. Система отсчёта. Перемещение.
Материальная точка. Система отсчёта. Перемещение. Паровой двигатель
Паровой двигатель Основы оптики
Основы оптики Подготовка швейной машины к работе. Урок технологии для 5 класса
Подготовка швейной машины к работе. Урок технологии для 5 класса Презентация по физике "Зеркала" - скачать
Презентация по физике "Зеркала" - скачать