Содержание
- 2. Турбулентное и ламинарное течение Критерий Рейнольдса Re = dwρ/μ d - диаметр; w - скорость потока;
- 3. Турбулентность Турбуле́нтность (лат.. turbulentus — бурный, беспорядочный)- явление, заключающееся в том, что, обычно, при увеличении скорости
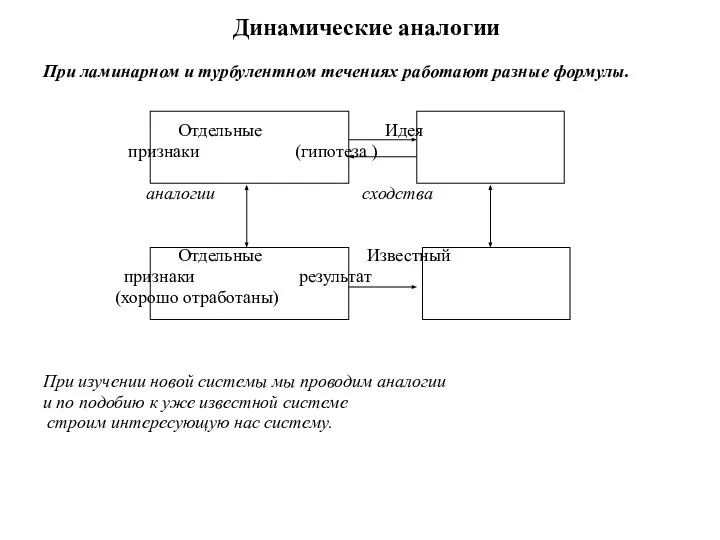
- 4. Динамические аналогии При ламинарном и турбулентном течениях работают разные формулы. Отдельные Идея признаки (гипотеза ) аналогии
- 5. Методы получения критериев подобия. Метод основан на использовании: а). π - теоремы (теоремы Букингема) б). Метода
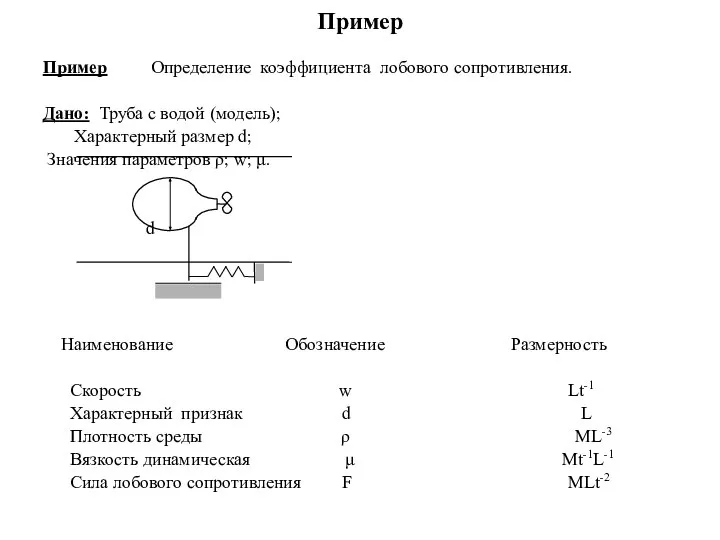
- 6. Пример Пример Определение коэффициента лобового сопротивления. Дано: Труба с водой (модель); Характерный размер d; Значения параметров
- 7. Есть некая функция, которая определяет силу лобового сопротивления как ϕ(wa, db, ρc, μλ) = F Определим
- 8. π - теорема Всякое полное уравнение физического процесса записанное в определенной системе единиц может быть представлена
- 9. Пусть P1,..., Pk - независимые параметры; Pk+1,..., Pm - зависимые параметры. Pk+1,..., Pm. следует выразить через
- 10. [P0,k+1] = ψk+1{[P01],...,[P0k]} . . . . . . . . . . [P0,s] = ψs{[P01],...,[P0k]}
- 11. Пусть k = q ln[a] = ln[b] = . . . . ln[q] = Определяем [a],[b],...,[q]
- 12. k [P0,s] = ∏[P0i]Di,s/D i=1 Di,k+1/D = xi Di,s/D = yi Di,m/D = zi k [P0,k+1]
- 13. Пусть P1 = P01 P2 = P02 . . . . Pk = P0k k k
- 14. Планирование эксперимента; основные понятия
- 15. Планирование эксперимента Основные понятия. - Активный эксперимент - Пассивный эксперимент Основная идея активного эксперимента - добиться
- 16. 4. Область определения. Нормированные переменные. Пусть xj*- реальные факторы xj - нормированные факторы -1≤ xj ≤
- 17. М - информационная матрица плана X размерности (k+1)×(k+1) det(A-λI) = 0 где λ - корни характеристического
- 18. Пример Пусть модель y(a,x) = a0 + a1x1 + a2x2 +... + anxn x0 = 0
- 19. 8. Критерий планирования эксперимента. План эксперимента зависит от выбранного критерия. Критерий в основном определяет либо требования
- 20. Полный (простой) факторный эксперимент. Факторы - число n (n=3) Уровни (2) - (значения факторов - +1,
- 21. Планы для квадратичных моделей. Композиционный план второго порядка y = a0 + a1x1 + a2x2 +
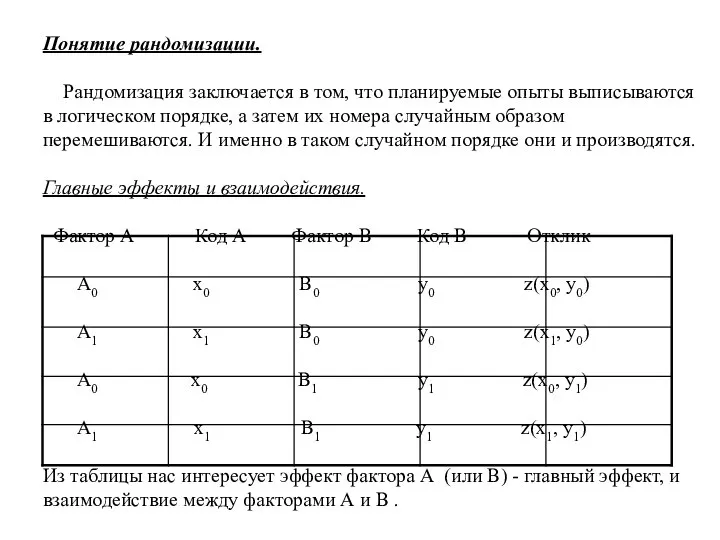
- 22. Понятие рандомизации. Рандомизация заключается в том, что планируемые опыты выписываются в логическом порядке, а затем их
- 23. Главный эффект фактора А пропорционален разности между: а) средним значением по всем откликам, включающим обработку фактора
- 24. Греко-латинские квадраты. Латинский квадрат. Пусть имеются 3 фактора - P, L, S, и 4 уровня -
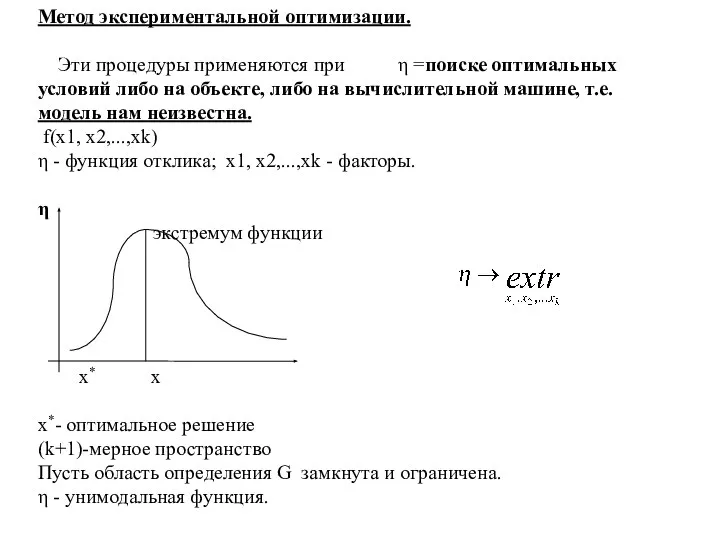
- 25. Метод экспериментальной оптимизации. Эти процедуры применяются при η =поиске оптимальных условий либо на объекте, либо на
- 26. Метод Бокса-Уилсона. Идея метода заключается в использовании метода крутого восхождения в сочетании с последовательно планируемым факторным
- 27. m – номер итерации α влияет на шаг. - оператор Набла Δх нужно подсчитать
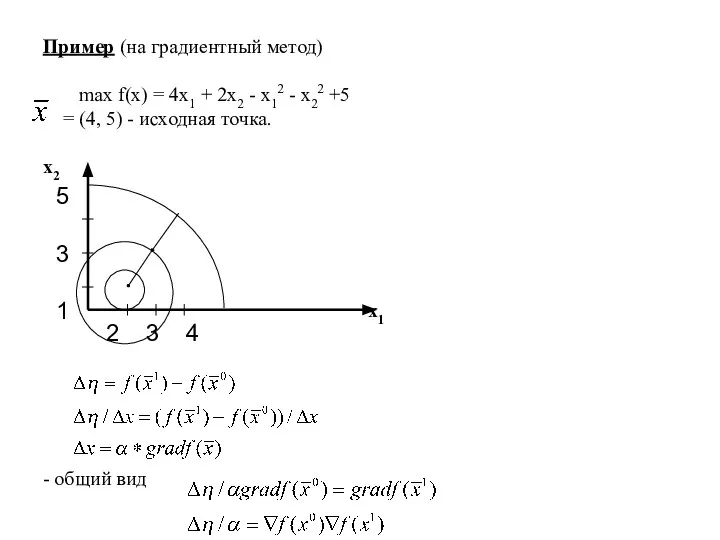
- 28. Пример (на градиентный метод) max f(x) = 4x1 + 2x2 - x12 - x22 +5 =
- 29. ∂f/∂x1 = 4 - 2x1 ∂f/∂x2 = 2 - 2x2 ∇f(x0) = (4-2*4, 2-2*5) = (-4,
- 30. Оценивание градиента. Если функция η(x1, x2,..., xk), где x1, x2,..., xk - размерные величины, то перейдем
- 31. x2 x1 - из регрессионной модели - из разложения в ряд Тейлора Проведя факторный эксперимент и
- 32. Метод интегральных аналогов. Для получения критериев подобия по методу интегральных аналогов необходимо знать уравнения системы или
- 34. Пренебрегаем индексом 1; Разделим члены уравнения на - число подобия Струхаля - число подобия Фруда -
- 35. Фракталы. Размерность Хаусдорфа-Безиковича.
- 36. Введение Автор понятия и первых работ по фрактальной геометрии Бенуа Мандельброт Нестрогое определение: Фрактал - это
- 37. IFS (Iterated Functions Systems) Kern: xk+1= Fx (xk, yk) yk+1= Fy (xk, yk) Mandel / Julia
- 38. Примеры фракталов
- 39. 3D
- 41. Скачать презентацию






![[P0,k+1] = ψk+1{[P01],...,[P0k]} . . . . . . . .](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1457352/slide-9.jpg)
![Пусть k = q ln[a] = ln[b] = . . .](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1457352/slide-10.jpg)
![k [P0,s] = ∏[P0i]Di,s/D i=1 Di,k+1/D = xi Di,s/D = yi](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1457352/slide-11.jpg)













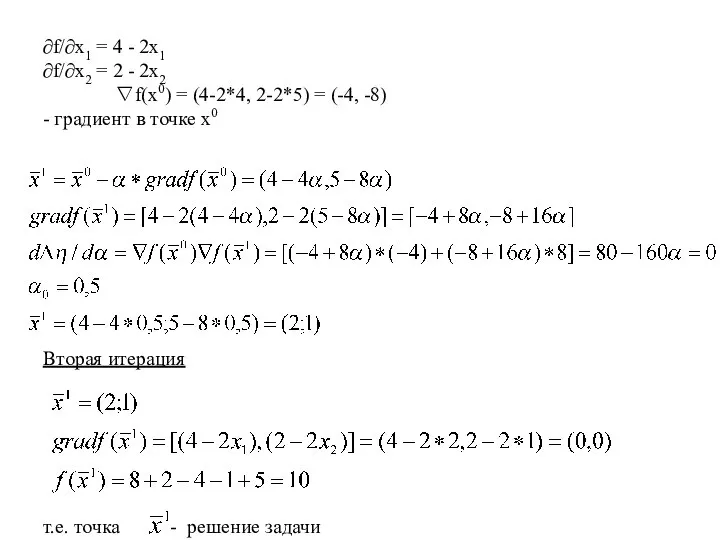










 Передача и использование электроэнергии
Передача и использование электроэнергии Самоиндукция. Индуктивность
Самоиндукция. Индуктивность Основные понятия и уравнения кинематики
Основные понятия и уравнения кинематики Електростатичне поле
Електростатичне поле  Пара сил. (Лекция 3)
Пара сил. (Лекция 3) Динамика кристаллической решетки
Динамика кристаллической решетки Аттестационная работа. «Электролиз. Применение электролиза»
Аттестационная работа. «Электролиз. Применение электролиза» Исследовательский проект Машина Голдберга Ловите привет!
Исследовательский проект Машина Голдберга Ловите привет! Неравновесные состояния и необратимые процессы. Броуновское движение
Неравновесные состояния и необратимые процессы. Броуновское движение Фотоэлектрические gреобразователи
Фотоэлектрические gреобразователи МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ О
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ О Радиоактивность. Строение атома
Радиоактивность. Строение атома klass_Magnitnoe_pole_Magnitnoe_pole_toka_Magnitnye_linii
klass_Magnitnoe_pole_Magnitnoe_pole_toka_Magnitnye_linii Давление на примере ЦПГ
Давление на примере ЦПГ Тепломассообмен. Теория подобия физических явлений. Числа подобия. Уравнения подобия
Тепломассообмен. Теория подобия физических явлений. Числа подобия. Уравнения подобия Электрическая дуга
Электрическая дуга Атомная физика
Атомная физика Аномальные свойства воды
Аномальные свойства воды Магнитное поле
Магнитное поле Новое состояние материи – кварк-глюонная плазма
Новое состояние материи – кварк-глюонная плазма Циклотрон
Циклотрон Презентация по физике "Электротехника" - скачать бесплатно
Презентация по физике "Электротехника" - скачать бесплатно Классификация способов обработки материалов потоками излучения
Классификация способов обработки материалов потоками излучения Презентация Ультрафиолетовые лучи
Презентация Ультрафиолетовые лучи  Расчет стержневых конструкций по предельному равновесию
Расчет стержневых конструкций по предельному равновесию Методы разделения белковых смесей. Хроматография
Методы разделения белковых смесей. Хроматография Творческий проект ученицы 9-а класса Симоновой Ольги. Учитель: Кенжина Н. М. Учитель информатики: Умнова Т.С.
Творческий проект ученицы 9-а класса Симоновой Ольги. Учитель: Кенжина Н. М. Учитель информатики: Умнова Т.С. Кристаллы. Образование кристаллов
Кристаллы. Образование кристаллов