Содержание
- 2. Общая физика Механика Молекулярная физика Электричество и магнетизм Оптика Физика атомов и атомных явлений Физика атомного
- 3. Структура дисциплины «Механика» Введение. Механика – раздел курса общей физики Кинематика материальной точки Динамика материальной точки
- 4. ОСНОВНАЯ ЛИТЕРАТУРА УЧЕБНИКИ Савельев И.В. Курс общей физики, т.1. Механика. Молекулярная физика Сивухин Д.В. Общий курс
- 5. ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА Белянкин А. Г., Матвеев А. Н., Сараева И. М., Устинова А. В., Шушурин С.
- 6. 1. Введение. Механика - раздел курса общей физики 1.1. Физические величины 1.2. Системы физических величин 1.3.
- 7. Задачи и методы физики Задача физики состоит в создании в нашем сознании такой модельной картины физического
- 8. Физические величины и их измерение Свойства и качества, которыми оперирует физика, называются физическими величинами. Измерением физических
- 9. Основные величины и единицы измерения Международной системы единиц (СИ) Длина (размерность – L) – величина, характеризующая
- 10. Основные величины и единицы измерения Международной системы единиц (СИ) Сила электрического тока (размерность – I) –
- 11. Основные величины и единицы измерения Международной системы единиц (СИ) Количество вещества (размерность n) – величина, равная
- 12. Дополнительные величины и единицы Плоский угол α – геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими
- 13. Механика – наука о движении и равновесии тел. Под движением в механике понимают простейшую форму изменение
- 14. Механика: от Ньютона до Эйнштейна Исаак Ньютон (1643 – 1727) Альберт Эйнштейн (1879 – 1955)
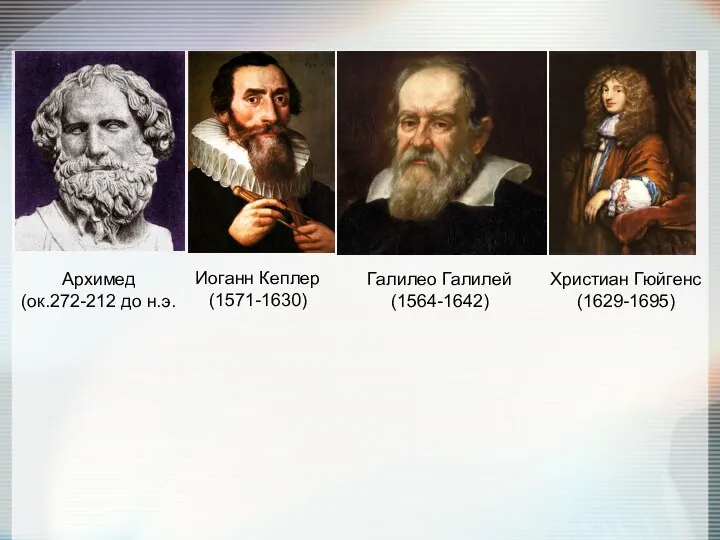
- 15. Архимед (ок.272-212 до н.э. Иоганн Кеплер (1571-1630) Галилео Галилей (1564-1642) Христиан Гюйгенс (1629-1695)
- 16. 2. Кинематика материальной точки
- 17. Кинема́тика – раздел механики, изучающий математическое описание движения идеализированных тел, без рассмотрения причин движения (массы, сил
- 18. Пространство и время в физике определяются в общем виде как фундаментальные структуры координации материальных объек-тов и
- 19. Система отсчета Система отсчёта – это совокупность тела отсчёта, связанной с ним системы координат и системы
- 20. Материальная точка Материальной точкой называется макроскопическое тело, размеры которого настолько малы, что в рассматриваемом движении их
- 21. Материальное тело Материальное тело – совокупность материальных точек, которые могут быть идентифицированы и отличны друг от
- 22. Основные системы координат на плоскости Декартова (прямоугольная) система координат Полярная система координат Преобразование от полярных координат
- 23. Основные системы координат в пространстве Декартова (прямоугольная) система координат Сферическая система координат Цилиндрическая система координат Преобразование
- 25. Скорость и ускорение при прямолинейном движении Средняя скорость Мгновенная скорость Ускорение
- 26. Примеры Пример 1. Неподвижная материальная точка. Пример 2. Равномерное движение.
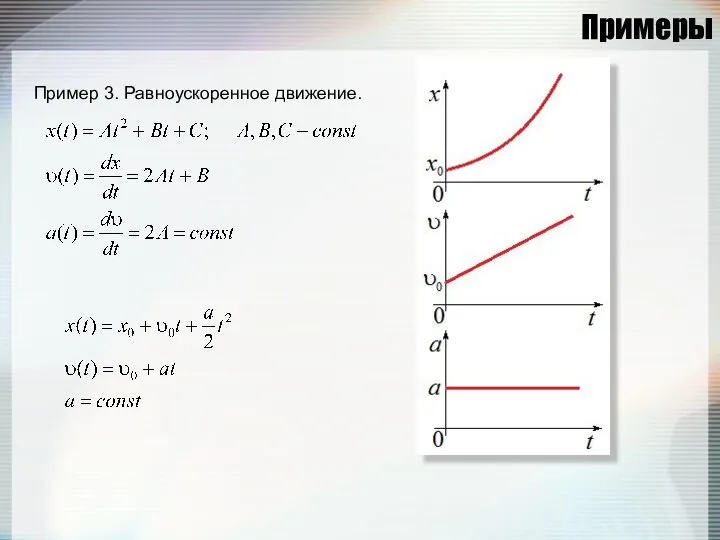
- 27. Примеры Пример 3. Равноускоренное движение.
- 28. Движение по окружности Угловая скорость Угловое ускорение Угловая координата Равномерное вращение:
- 29. Связь угловых и линейных величин при вращении S – длина дуги окружности XM R – радиус
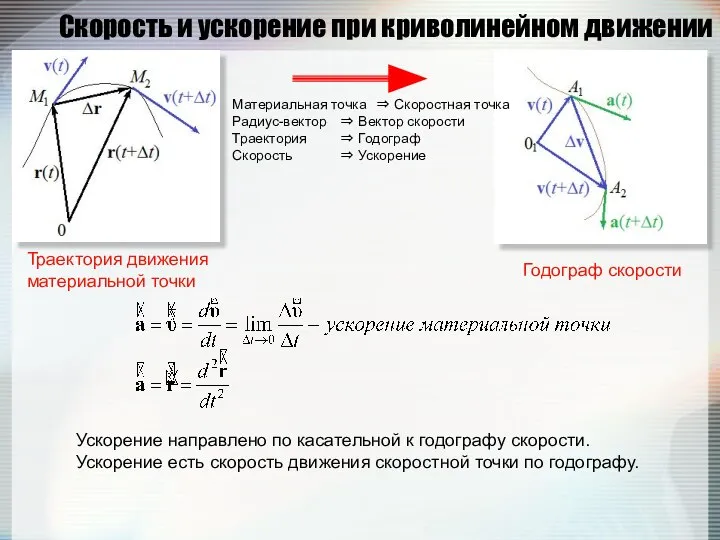
- 30. Скорость и ускорение при криволинейном движении Мгновенная скорость есть вектор, направленный по касательной к траектории движущейся
- 31. Скорость и ускорение при криволинейном движении Ускорение направлено по касательной к годографу скорости. Ускорение есть скорость
- 32. где R называется радиусом кривизны траектории Ускорение можно представить в виде геометрической суммы нормального и тангенциального
- 33. Векторы угловой скорости и углового ускорения при движении по окружности Эти формулы справедливы только в случае,
- 34. Тема 3. Динамика материальной точки Первый закон Ньютона. Инерциальные системы отсчета. Масса, импульс, сила в классической
- 35. Динамика – раздел механики, изучающий движение тел совместно с физическими причинами, вызывающими это движение
- 36. Первый закон Ньютона (Закон инерции) Тело (материальная точка), не подверженное внешним воздействиям, либо находится в покое,
- 37. Инерциальные системы отсчета Существует система отсчета, в которой все свободные тела движутся прямолинейно и равномерно. Такая
- 38. Масса Свойство тел оказывать сопротивление при попытках привести его в движение или изменить модуль или направление
- 39. Изолированная (замкнутая) система Изолированная (замкнутая) система – это система материальных тел, на которые не действуют внешние
- 40. Импульс материальной точки Импульсом (количеством движения) материальной точки называется вектор, равный произведению массы материальной точки на
- 41. Понятие силы В динамике Ньютона не скорость, а изменение скорости, т. е. ускорение, имеет причину. Причиной
- 42. Виды силовых взаимодействий 1.Гравитационное 2. Электромагнитное 3. Сильное 4. Слабое Сильные и слабые взаимодействия проявляются в
- 43. Второй закон Ньютона Качественное определение силы: Под силой в механике понимают всякую причину, изменяющую импульс движущегося
- 44. Третий закон Ньютона Рассмотрим замкнутую систему двух взаимодействующих точек. Закон сохранения импульса в этом случае: Дифференцируем
- 45. Преобразования Галилея Преобразования Галилея Нерелятивистский закон сложения скоростей
- 46. Принцип относительности Галилея Ускорение инвариантно относительно преобразований Галилея Сила инвариантна относительно преобразований Галилея Принцип относительности Галилея:
- 47. Упругие силы Под действием приложенных сил реальное тело деформируется, т.е. изменяет свои размеры и форму. Если
- 48. Упругие деформации Деформация однородного стержня Относительное удлинение Механические напряжения: Нормальное напряжение Тангенциальное напряжение S – площадь
- 49. Силы трения Трение, возникающее при относительном перемещении двух соприкасающихся тел, называется внешним трением. Трение между частями
- 50. Сухое трение Максимальная сила трения покоя, а также сила трения скольжения не зависят от площади соприкосновения
- 51. Вязкое трение Зависимость силы трения от скорости скольжения При малых скоростях: При больших скоростях: Помимо собственно
- 52. Сила тяжести. Вес тела Сила тяжести: Вектор g – ускорение свободного падения. Сила P, с которой
- 53. Тема 4. Законы сохранения Кинетическая энергия. Работа. Консервативные силы. Потенциальная энергия во внешнем поле сил. Потенциальная
- 54. Сохраняющиеся величины Внешние силы – силы, действующие на систему тел со стороны тел, не входящих в
- 55. Кинетическая энергия Рассмотрим систему, состоящую из одной материальной точки. Уравнение движения: Умножим на перемещение В случае
- 56. Работа
- 57. Консервативные силы
- 58. Потенциальная энергия во внешнем поле сил
- 59. Потенциальная энергия взаимодействия
- 60. Закон сохранения энергии
- 61. Потенциальная энергия взаимодействия
- 62. 4. Система материальных точек Под системой материальных точек (СМТ) будем понимать конечное число взаимодействующих тел, которые
- 63. Внешние и внутренние силы Из 2-го закона Ньютона следует: Производная по времени от импульса СМТ равна
- 64. Импульс силы Если сила F(e) постоянная, то Произведение постоянной силы F(e) на время ее действия называется
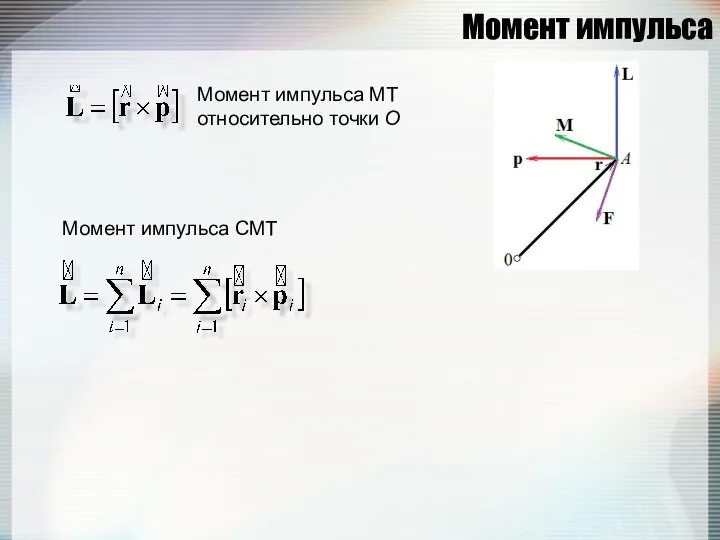
- 65. Момент импульса Момент импульса МТ относительно точки О Момент импульса СМТ
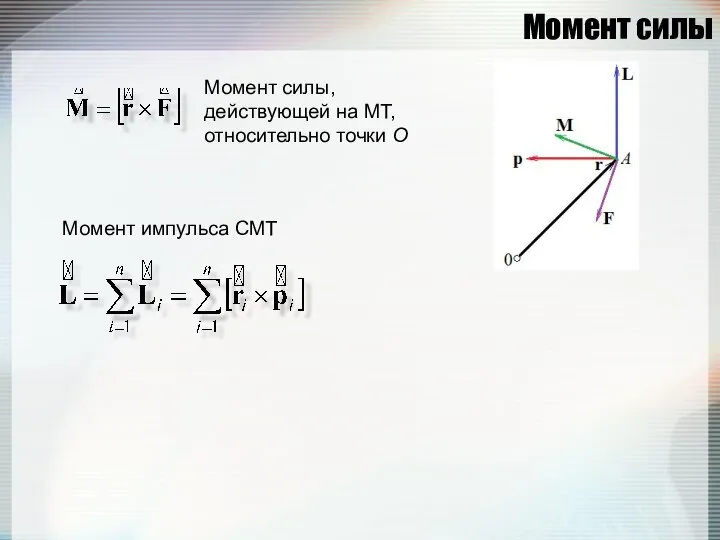
- 66. Момент силы Момент силы, действующей на МТ, относительно точки О Момент импульса СМТ
- 67. Момент силы
- 68. Тема 5. Неинерциальные системы отсчета Неинерциальной системой отсчета (НСО) называется система, движущаяся ускоренно относительно инерциальной. Тело
- 69. Силы инерции В ИСО единственной причиной ускоренного движения тела являются силы, действующие со стороны других тел.
- 70. НСО, движущиеся прямолинейно-поступательно a’ – ускорение в НСО (относительное ускорение), a – ускорение в ИСО (абсолютное
- 71. Неинерциальные вращающиеся системы отсчета Отличие вращающихся НСО обуславливается тем, что переносная скорость различных точек вращающейся системы
- 72. Неинерциальные вращающиеся системы отсчета Дифференцируем по времени Находим абсолютное ускорение:
- 73. Силы инерции
- 74. Тема 6. Механика твёрдого тела
- 75. Степени свободы твердого тела Абсолютно твердое тело (ТТ) – неизменяемая система материальных точек, т.е. идеализированная система,
- 76. Кинематика твердого тела При поступательном движении скорости всех точек тела в любой момент времени одинаковы. Любая
- 77. Движение твердого тела В плоском движении положение ТТ полностью определяется положением отрезка прямой, жестко связанно с
- 78. Движение центра масс твердого тела Центром масс (центром инерции) СМТ называется точка С, положение которой задается
- 79. Вращение тела вокруг неподвижной оси Рассмотрим твердое тело, которое может вращаться вокруг неподвижной оси Z. Производная
- 80. Момент инерции Величина, равная сумме произведений элементарных масс (масс материальных точек) на квадраты их расстояний от
- 81. Момент инерции Для тела любой формы и с произвольным распределением массы существуют три взаимно перпендикулярные, проходящие
- 82. Момент инерции Для твердого тела: Примеры моментов инерции тел
- 83. Теорема Гюйгенса-Штейнера Момент инерции J относительно произвольной оси равен сумме момента инерции Jc относительно оси, параллельной
- 84. Тензор инерции В общем случае несимметричного тела векторы момента импульса и угловой скорости не совпадают по
- 85. Кинетическая энергия вращающегося твердого тела Для плоского движения: Кинетическая энергия тела при плоском движении складывается из
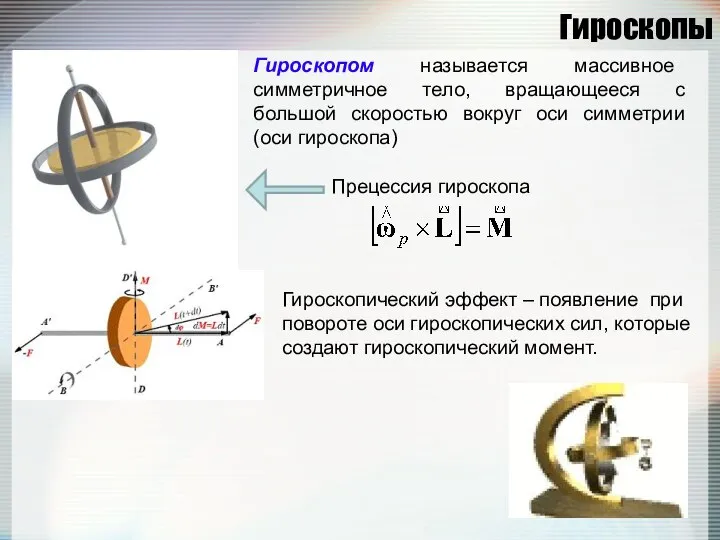
- 86. Гироскопы Гироскопом называется массивное симметричное тело, вращающееся с большой скоростью вокруг оси симметрии (оси гироскопа) Гироскопический
- 87. Тема 7. Всемирное тяготение
- 88. Закон всемирного тяготения Сила, с которой две материальные точки притягиваются друг к другу, пропорциональна массам этих
- 89. Закон всемирного тяготения Для определения силы взаимодействия протяженных тел их нужно разбить на элементарные массы Δm,
- 90. Гравитационное поле Гравитационное взаимодействие осуществляется через гравитацион-ное поле. Всякое тело изменяет свойства окружающего его пространства путем
- 91. Гравитационное поле Потенциальная энергия взаимодействия масс M и m: Потенциал гравитационного поля: Работа поля по перемещению
- 92. Принцип эквивалентности Все физические явления в однородном поле тяготения происходят совершенно так же, как и в
- 93. Космические скорости Для того, чтобы двигаться вокруг Земли по круговой орбите вблизи радиуса Земли, тело должно
- 94. Тема 8. Колебательное движение
- 95. Колебательный процесс Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. В зависимости от физической природы
- 96. Колебательный процесс Свободными (собственными) колебаниями называются колебания, происходящие в системе, предоставленной самой себе после того, как
- 97. Гармонические колебания Гармоническими называются колебания, при которых колеблющаяся величина (например, отклонение маятника) изменяется со временем по
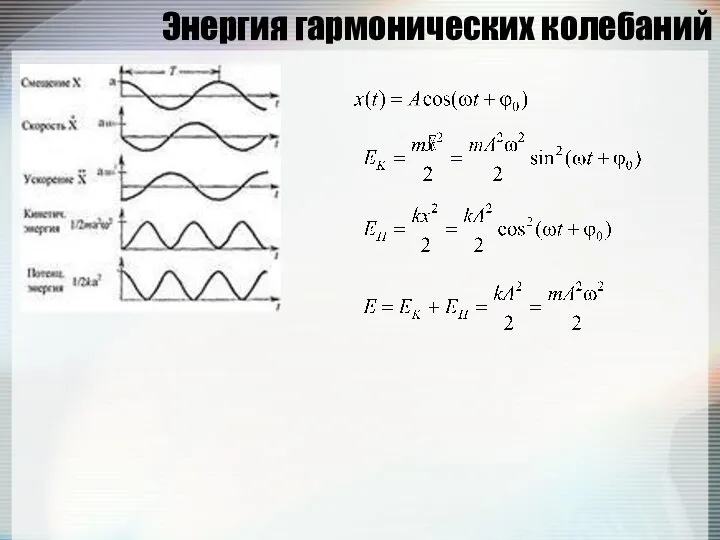
- 98. Энергия гармонических колебаний
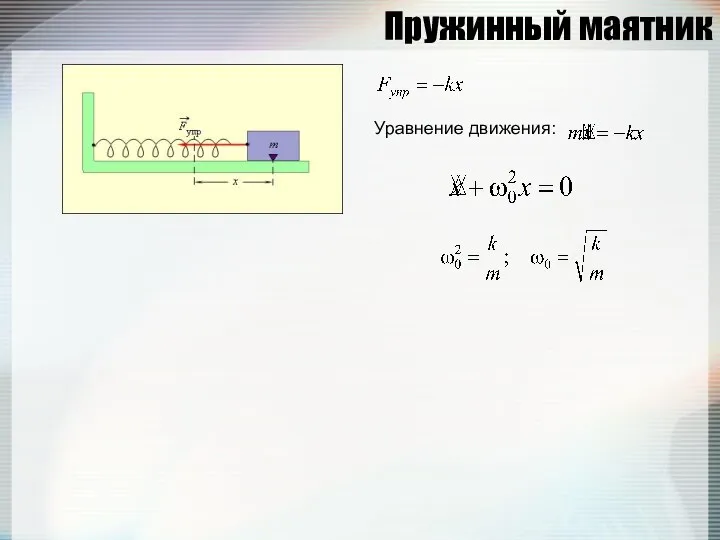
- 99. Пружинный маятник Уравнение движения:
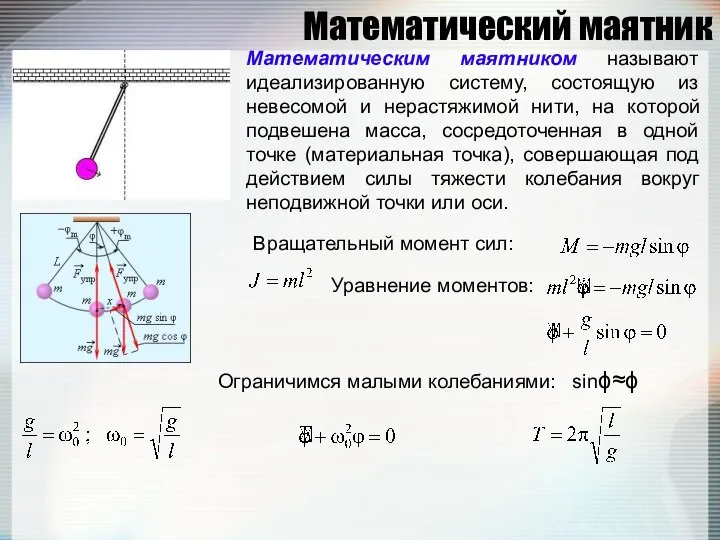
- 100. Математический маятник Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена
- 101. Физический маятник Физическим маятником называют твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки
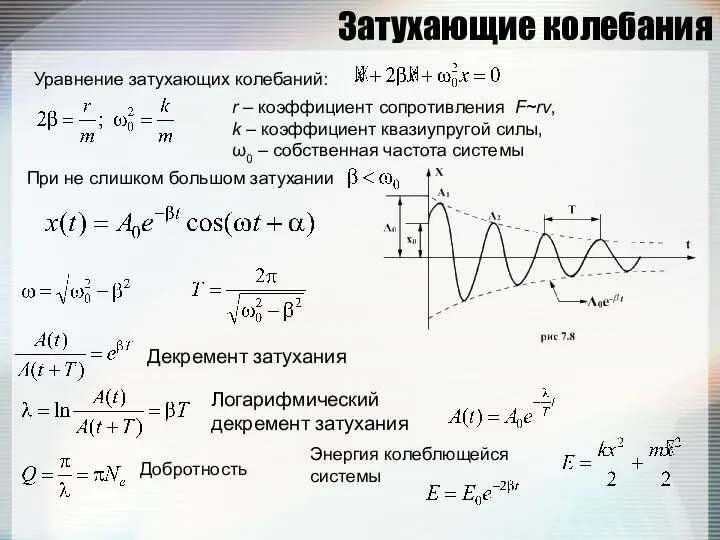
- 102. Затухающие колебания Уравнение затухающих колебаний: r – коэффициент сопротивления F~rv, k – коэффициент квазиупругой силы, ω0
- 103. Вынужденные колебания
- 105. Скачать презентацию




























































































 Биосенсоры
Биосенсоры Аттестационная работа. Организация исследовательской деятельности обучающихся по физике Главное не табличка, а привычка
Аттестационная работа. Организация исследовательской деятельности обучающихся по физике Главное не табличка, а привычка Анималистика в металлопластике
Анималистика в металлопластике Аттестационная работа. Проектная деятельность на уроках физики и во внеурочной деятельности по предмету
Аттестационная работа. Проектная деятельность на уроках физики и во внеурочной деятельности по предмету Инфракрасное излучение
Инфракрасное излучение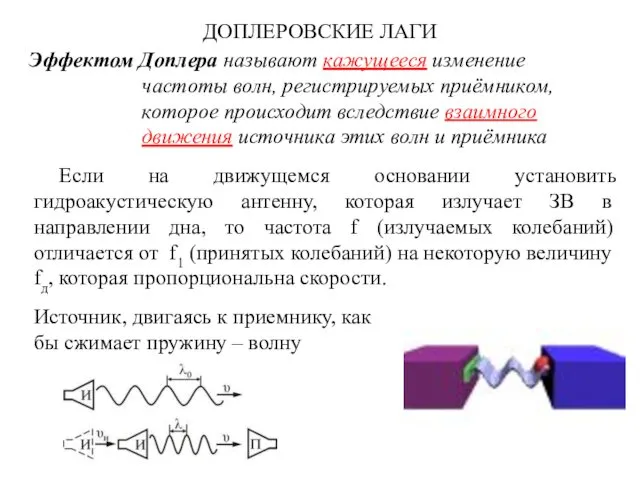 Доплеровские лаги
Доплеровские лаги Аттестация 1-2012. Вопросы теста
Аттестация 1-2012. Вопросы теста Открытие нейтрона и протона
Открытие нейтрона и протона Plasmonics
Plasmonics Сила тока. Единицы силы тока и её измерение
Сила тока. Единицы силы тока и её измерение Техническое обслуживание распределительных устройств свыше 1 кВ
Техническое обслуживание распределительных устройств свыше 1 кВ Скорость света
Скорость света Имитация случайных величин и процессов. Базовые датчики. Лекция №3
Имитация случайных величин и процессов. Базовые датчики. Лекция №3 Поширення електромагнітних хвиль над пласкою ідеально провідною поверхнею
Поширення електромагнітних хвиль над пласкою ідеально провідною поверхнею Перспективы развития и использования электроэнергетики в современном мире Проектная работа учащегося 11 класса МОУ Вязовской с
Перспективы развития и использования электроэнергетики в современном мире Проектная работа учащегося 11 класса МОУ Вязовской с Техническое обслуживание и ремонт с/х машин и оборудования
Техническое обслуживание и ремонт с/х машин и оборудования Эксперимент Томсона. Определение удельного заряда электрона
Эксперимент Томсона. Определение удельного заряда электрона Движение тела по окружности с постоянной по модулю скоростью.
Движение тела по окружности с постоянной по модулю скоростью. Магнитное поле в вакууме
Магнитное поле в вакууме Лекция №9 (9 ). Волновые явления вблизи границы раздела сред
Лекция №9 (9 ). Волновые явления вблизи границы раздела сред Термодинаміка. Перший закон термодинаміки
Термодинаміка. Перший закон термодинаміки ФОТОЭФФЕКТ. Люминисценция және оның негізгі заңдылықтары. Қара дененің сәуле шығару заңдары. (Лекция 15)
ФОТОЭФФЕКТ. Люминисценция және оның негізгі заңдылықтары. Қара дененің сәуле шығару заңдары. (Лекция 15) Давление твердых тел
Давление твердых тел  Механика. Кинематика - начальные понятия
Механика. Кинематика - начальные понятия &
& Физика Космоса
Физика Космоса Расчет КИХ-фильтров с окном Кайзера
Расчет КИХ-фильтров с окном Кайзера Электротехника. Операторный метод анализа переходных процессов. (Лекция 13)
Электротехника. Операторный метод анализа переходных процессов. (Лекция 13)