Лекция 2-2022

§ 2.1. Мотивировка
Первоначально понятие грамматики было формализовано лингвистами при изучении

Надеялись, что, заложив в компьютер формальную грамматику, например, англий-ского языка,

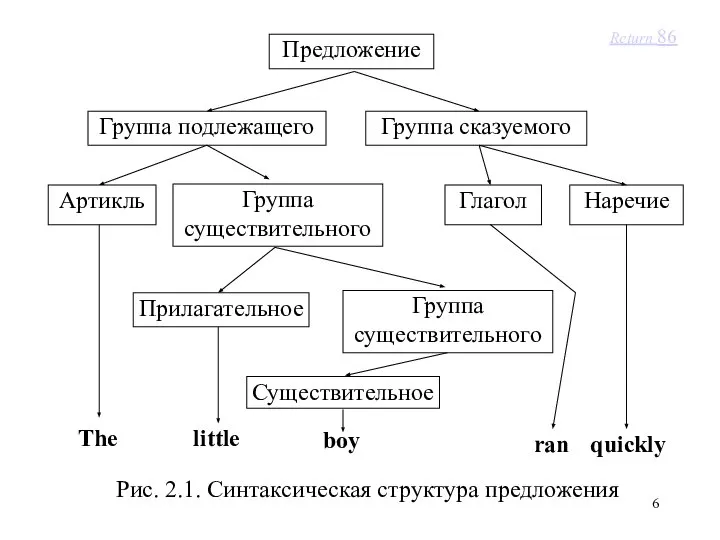
Грамматический разбор

Из школьного опыта известно, что собой представляет грамматический разбор предло-жения.

При разборе мы имеем дело с грамматическими категориями:
‘предложение’, ‘группа существительного’,

Return 86

Правила грамматики

Грамматический разбор предложений подразу-мевает использование правил некоторой грам-матики. Мы

Механизм порождения

Здесь стрелочка → отделяет левую часть правила от правой,

Механизм порождения
Начиная с цепочки, включающей только грамматический термин,

§ 2.2. Грамматика. Язык, порождаемый грамматикой

1) нетерминалы — грамматические термины

3) правила, левые и правые части которых состоят из нетерминалов и

Грамматики. Выводимость.

Определение 2.1. Грамматикой назы-вается четверка G = (VN, VT,

Грамматики. Выводимость.

Грамматики. Выводимость.

Выводимость

Выводимость

Если мы хотим подчеркнуть, что такой вывод использует по крайней мере

Напомним, что для любого отношения R имеют место следующие тождества:

Язык, порождаемый грамматикой

Пример 2.1.

Рассмотрим грамматику G = (VN, VT, P, S),
где

Грамматику, определённую в предыдущем параграфе, вслед за Н. Хомским назовем

Определение 2.7. Грамматика
G = (VN, VT, P, S)
является

Часто вместо термина “контекстно-зависимая грамматика” используют аббре-виатуру csg (context-sensitive grammar).

7: Наконец, применим n – 1 раз правило (7).

6: Применим один

Замечание 2.1. Некоторые авторы требуют, чтобы правила контекстно-зависимой грамматики имели

В отечественной литературе для таких грамматик чаще используется термин НС-грамматики

Грамматика, приведённая в примере 2.2, не является НС-грамматикой из-за того,

каждое вхождение терминала a∈VT заменить на новый нетерминал Z,

пополнить

Правило же вида
X1X2…Xm → Y1Y2…Ym+q
неукорачивающей грамматики, где
m

Замечание 2.2. Отметим, что новые правила с нетерминалами A могут

Пример 2.3. Покажем на примере, как построить НС-грамматику, эквиваленную неукорачивающей грамматике

Правило (3) заменим группой правил:
(3.1) CB → A1B, (3.2)

Определение 2.8. Грамматика
G = (VN, VT, P, S)
является

Замечание 2.3. Правило вида A → β позволяет заменить A

Грамматика, приведенная в примере 2.1, является не только грамматикой типа 0,

Пример 2.3. Рассмотрим интересную контекстно-свободную грамматику
G = (VN, VT, P,

Индукцией по длине цепочки покажем, что
L(G) = {x∈{a, b}+

База. Очевидно, что все три утверждения выполняются для всех x:

Индукционная гипотеза. Предположим, что утверждения 1–3 выполняются для всех x:
|

В случае (2.2) имеем
A bAA bx1A bx1x2 = x;

Достаточность. Пусть | x | = k + 1.
(1)

Регулярные грамматики

Определение 2.9. Грамматика
G = (VN, VT, P, S)

Замечание 2.4.
В лекции 3 будет определено абстрактное устройство, называемое

Пример rg

Пример 2.4. Рассмотрим грамматику
G = (VN, VT, P,

Ответ на вопрос

Нетерминал B порождает символ 0 или 1, которому

Наконец, нетерминал S порождает:
то же, что A, но с обязательным

Классы языков

Очевидно, что
каждая грамматика типа 3 является грамматикой

В соответствии с текущей практикой язык типа 3 или регулярный

Далее будет показано, что языки типа 0 соответствуют языкам, которые

§ 2.4. Пустое предложение

Грамматики определены так, что пустое предложение (ε)

Имеет место следующая лемма.
Лемма 2.1. Если G = (VN,

Доказательство. Пусть S1 — символ, не принадлежащий ни алфавиту нетерминалов,

Очевидно, что грамматики G и G1 имеют один и тот

Теорема 2.2. Если L — контекстно-зависимый, контекстно-свободный или регулярный язык,

Если язык L = L(G) не содержит пустого предложения, то

Правило S → ε может использоваться только как первое и

Если же L = L(G) содержит пустое предложение, то среди

Согласно лемме 2.1 типы грамматик G и G1 одинаковы, поэтому

Перестроим грамматику G из (сл.24) примера 2.2 согласно лемме 2.1

Построенная грамматика G1 отличается от исходной грамматики G только дополнительным

Мы можем добавить пустое предложе-ние к L(G1), пополнив грамматику G1

§ 2.5. Рекурсивность контекстно-зависимых грамматик

Определение 2.10. Грамматика
G = (VN,

Пусть G = (VN, VT, P, S) — контекстно-зависимая грамматика.

Если ε∈L(G), то мы можем образовать новую грамматику:
G1= (VN,

Предположим также, что j ≥ k×p
Тогда среди этих сентенциальных

Интуитивно ясно, что если существует какой-нибудь вывод терминальной цепочки, то

Теорема 2.3. Если грамматика
G = (VN, VT, P, S)

Очевидно, что
T0 = {S}, и при m > 0
Tm

Осталось доказать, что для некоторого m непременно будет Tm= Tm–1.

Таким образом, при некотором
m ≤ (k + 1)n
непременно

Пример 2.6. Рассмотрим грамматику G из примера 2.2.
С

Рассмотрим теперь наглядный метод описания любого вывода в контекстно-свободной грамматике.

Определение 2.11. Пусть
G = (VN, VT, P, S) —

4) если узлы n1, n2, ... , nk — прямые потомки

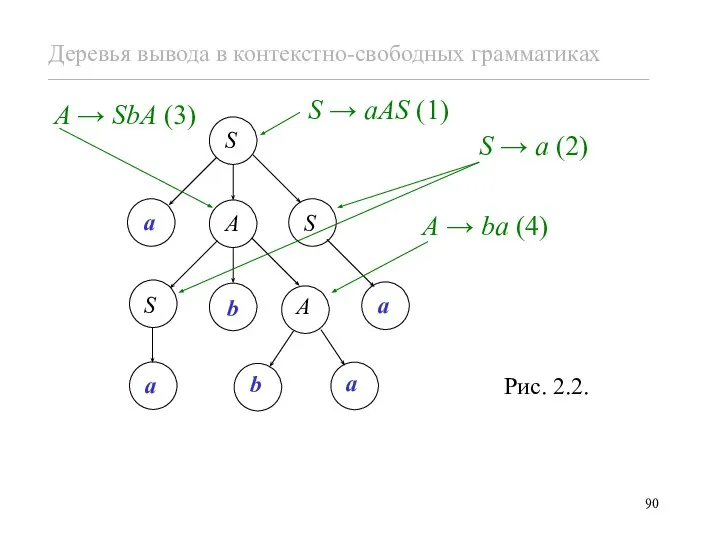
Пример 2.7. Рассмотрим КС-грамматику
G = ({S, A}, {a, b},

S → a (2)

A → ba (4)

S → aAS

Результат aabbaa этого дерева вывода получается, если выписать метки листьев

Если это вспомогательное утверждение будет доказано для любой грамматики GA,

Retrun to slade 49

Return 99

Return 97

Return 102

Индукционная гипотеза. Предположим, что утверждение выполняется для всех k ≤ n

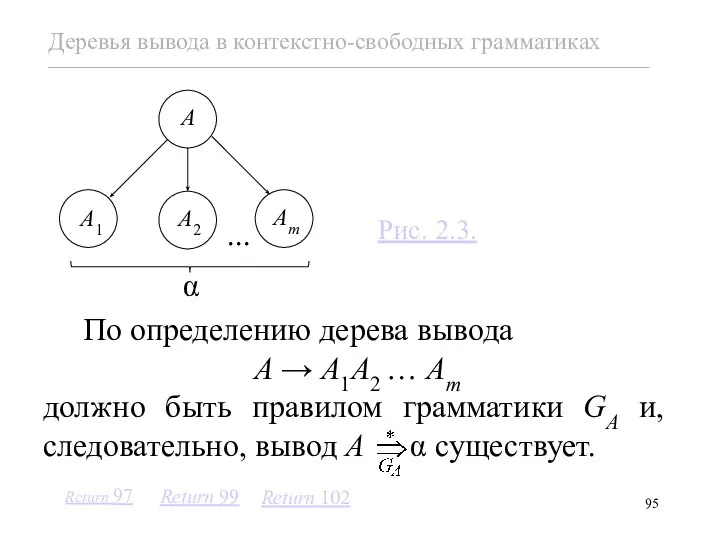
Рассмотрим прямых потомков корня данного дерева вывода (см. рис.2.3) .

Легко видеть, что если i < j, то узел i

Если li = 0, то αi = Ai.
Если