Содержание
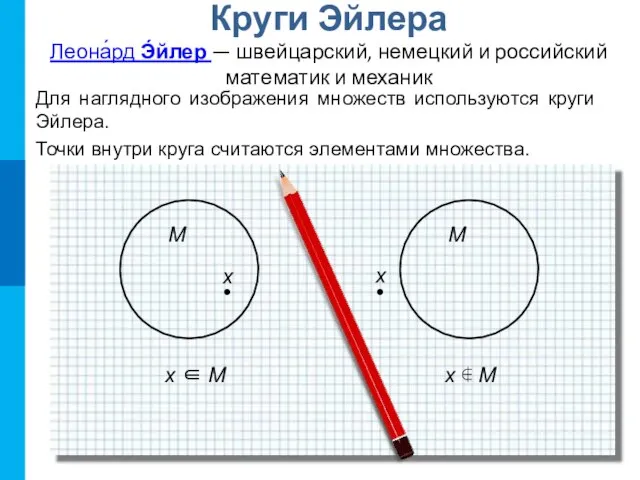
- 2. Круги Эйлера Леона́рд Э́йлер — швейцарский, немецкий и российский математик и механик Для наглядного изображения множеств
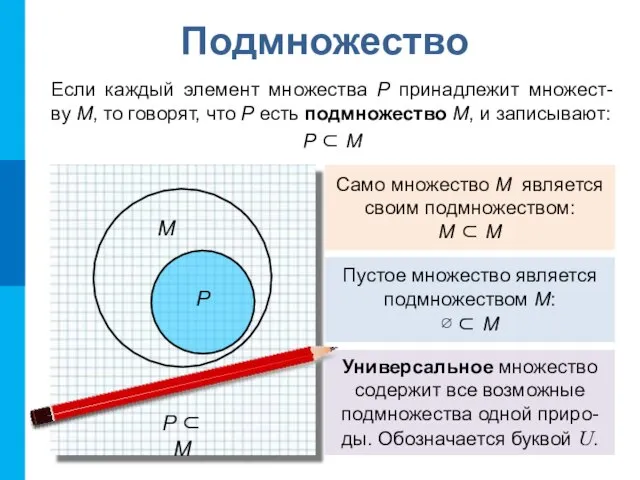
- 3. Подмножество Если каждый элемент множества P принадлежит множест- ву М, то говорят, что P есть подмножество
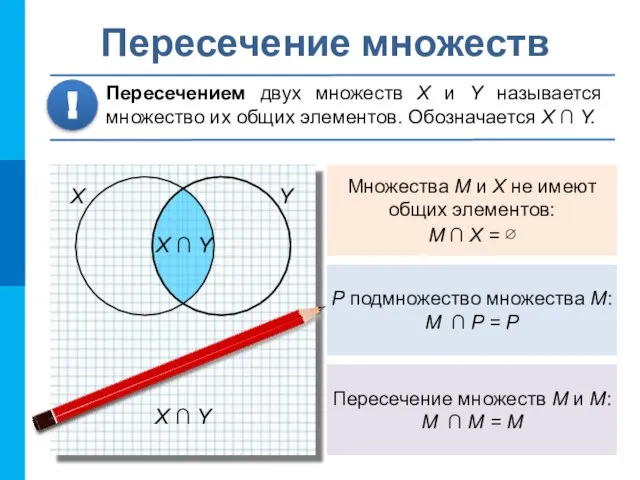
- 4. Множества M и X не имеют общих элементов: M ∩ X = ∅ P подмножество множества
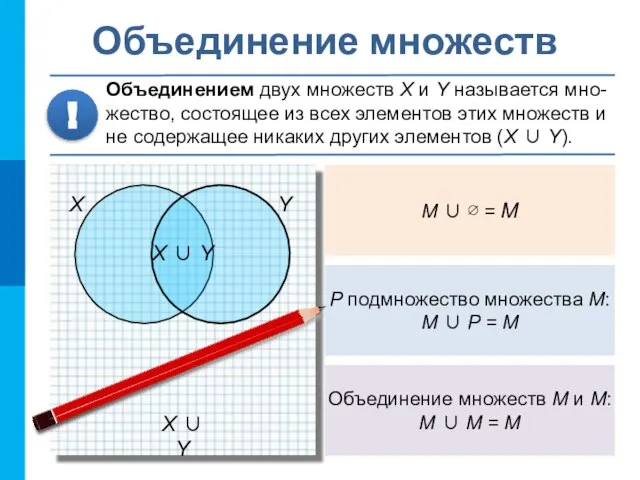
- 5. X ∪ Y Объединение множеств Объединением двух множеств X и Y называется мно-жество, состоящее из всех
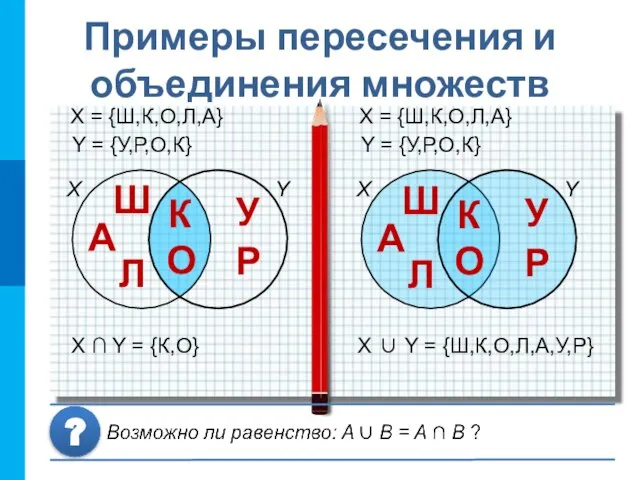
- 6. Примеры пересечения и объединения множеств X Y X ∪ Y = {Ш,К,О,Л,А,У,Р} X = {Ш,К,О,Л,А} Y
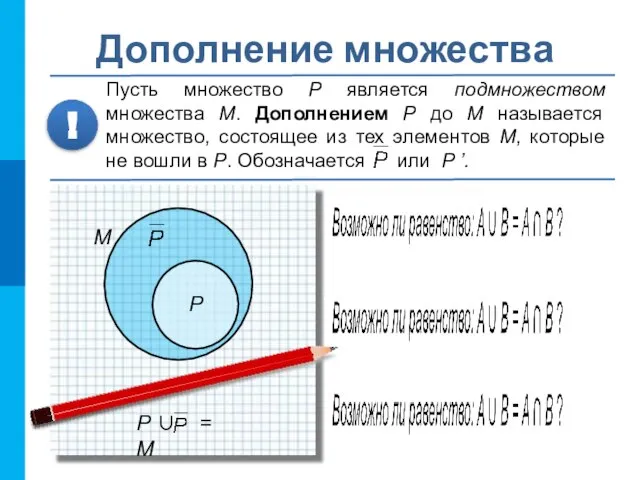
- 7. Дополнение множества Пусть множество P является подмножеством множества М. Дополнением P до М называется множество, состоящее
- 8. Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний. В алгебре логики высказывания обозначают
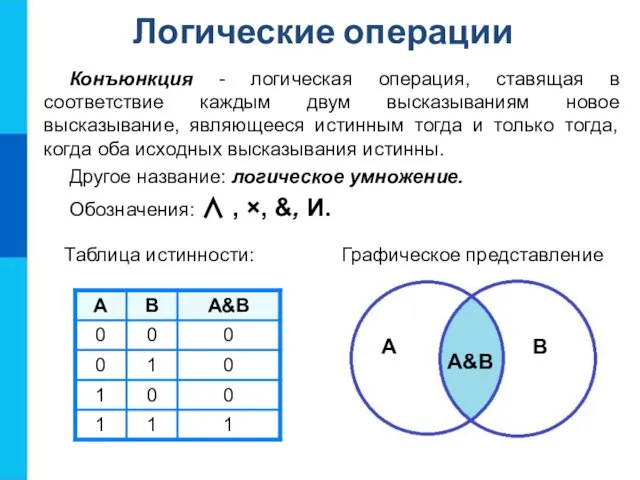
- 9. Конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и
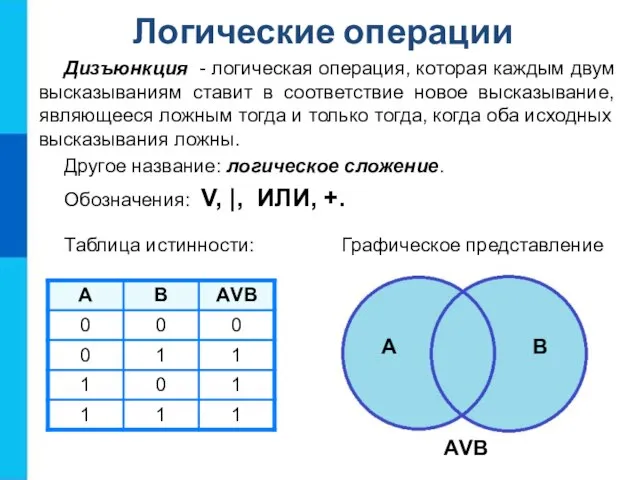
- 10. Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда
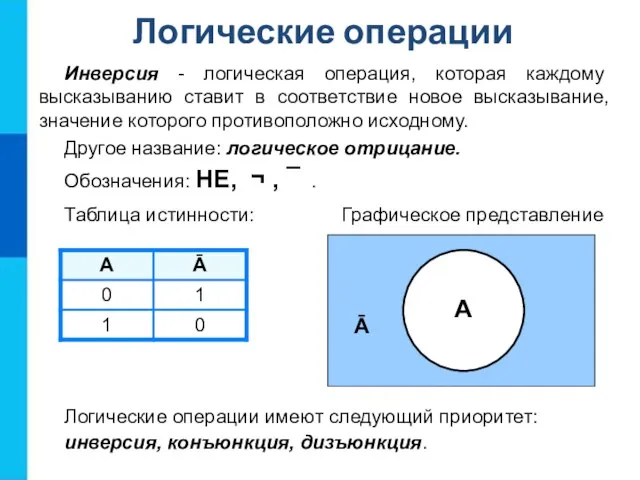
- 11. Инверсия - логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
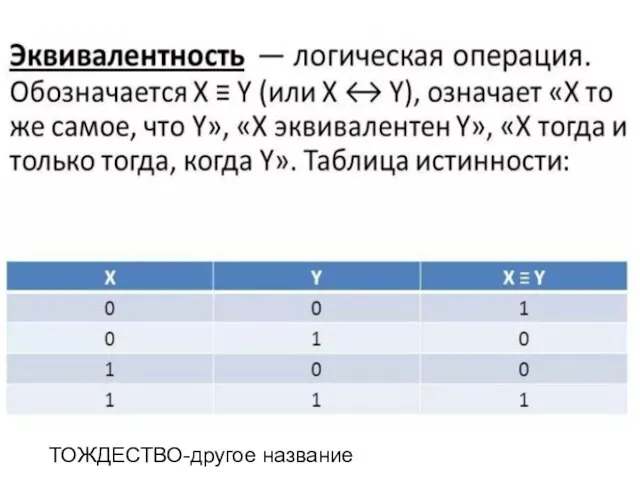
- 13. ТОЖДЕСТВО-другое название
- 14. Приоритет логических операций
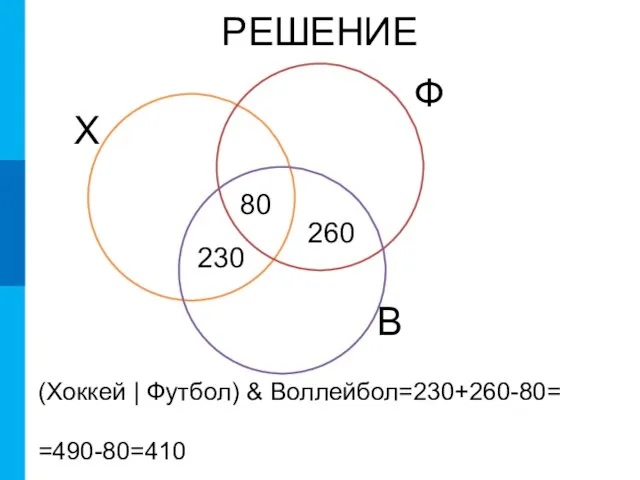
- 16. РЕШЕНИЕ Х Ф В 80 230 260 (Хоккей | Футбол) & Воллейбол=230+260-80= =490-80=410
- 17. Построение таблиц истинности для логических выражений подсчитать n - число переменных в выражении подсчитать общее число
- 18. А V A & B n = 2, m = 22 = 4. Приоритет операций: &,
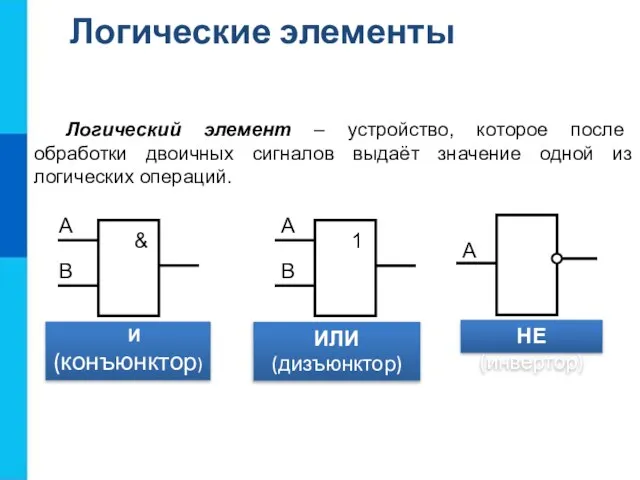
- 19. Логический элемент – устройство, которое после обработки двоичных сигналов выдаёт значение одной из логических операций. Логические
- 21. Скачать презентацию






 Основы композиции в графическом дизайне
Основы композиции в графическом дизайне Процессоры фирмы Intel до Pentium III
Процессоры фирмы Intel до Pentium III  Информация для детей и родителей
Информация для детей и родителей Презентация "Магистрально-модульный принцип построения компьютера" - скачать презентации по Информатике
Презентация "Магистрально-модульный принцип построения компьютера" - скачать презентации по Информатике HTTP и HTTPS
HTTP и HTTPS Создание страницы главного меню, товаров, заказов, контактов. (Занятие 8. Модуль 3)
Создание страницы главного меню, товаров, заказов, контактов. (Занятие 8. Модуль 3) Модуль для 1с-Битрикс. Руководство и настройка
Модуль для 1с-Битрикс. Руководство и настройка САПР. АСТПП. Интегрированные САПР/АСТПП
САПР. АСТПП. Интегрированные САПР/АСТПП Виды геометрических моделей, их свойства. Понятия о каркасном и твердотельном моделировании. (Лекция 6)
Виды геометрических моделей, их свойства. Понятия о каркасном и твердотельном моделировании. (Лекция 6) Информация, информационные процессы, измерение количества информации
Информация, информационные процессы, измерение количества информации Windows Hello for Everyone
Windows Hello for Everyone Практическая работа: Интерполяция в ГИС
Практическая работа: Интерполяция в ГИС Общение в Интернете. Корсакова Е. А., ГБОУ СОШ №1038
Общение в Интернете. Корсакова Е. А., ГБОУ СОШ №1038 Применение средств табличного процессора MS Excel для моделирования экономических ситуаций
Применение средств табличного процессора MS Excel для моделирования экономических ситуаций Растровое и векторное кодирование графической информации.
Растровое и векторное кодирование графической информации. Базы данных_Структура БД_Таблица БД 1 урок
Базы данных_Структура БД_Таблица БД 1 урок Системный оператор
Системный оператор Digital-агентство полного цикла
Digital-агентство полного цикла История развития компьютерных программ. Графические редакторы
История развития компьютерных программ. Графические редакторы Построение модели управленческого учета.
Построение модели управленческого учета. Основные алгоритмические конструкции (8 класс)
Основные алгоритмические конструкции (8 класс) Задачи, которые умеет решать 1С:Документооборот
Задачи, которые умеет решать 1С:Документооборот Школьный сайт – инструмент вхождения в единое информационное пространство Выполнила: Рухманова В.В. учитель физики и информати
Школьный сайт – инструмент вхождения в единое информационное пространство Выполнила: Рухманова В.В. учитель физики и информати Деректер қоры. Реляциялық деректер қорын басқару жүйелері
Деректер қоры. Реляциялық деректер қорын басқару жүйелері О применении контрольно-кассовой техники для интернет- магазинов
О применении контрольно-кассовой техники для интернет- магазинов Двоичное кодирование графической информации
Двоичное кодирование графической информации Графика в компьютере
Графика в компьютере Библиотека будущего
Библиотека будущего