Содержание
- 2. Введение ЛПР выбирает ту или иную альтернативу из множества возможных альтернатив. Критерий (или целевая функция) –
- 3. Введение Критерий k – функция от альтернативы a: k(a) Иногда удобно рассматривать несколько критериев в виде
- 4. Оптимальность по Парето Альтернатива аi является доминирующей по отношению к альтернативе аk ,если по всем критериям
- 5. Оптимальность по Парето 1. Указание верхних границ критериев. Дополнительная информация об оптимальном исходе а*∈D в этом
- 6. Оптимальность по Парето 2. Метод главного критерия. Критерии располагаются в порядке убывания важности: объявляется собственным критерием,
- 7. Оптимальность по Парето 3. Метод уступок. Располагаем критерии в порядке убывания важности: ….k1, k2… Считаем критерий
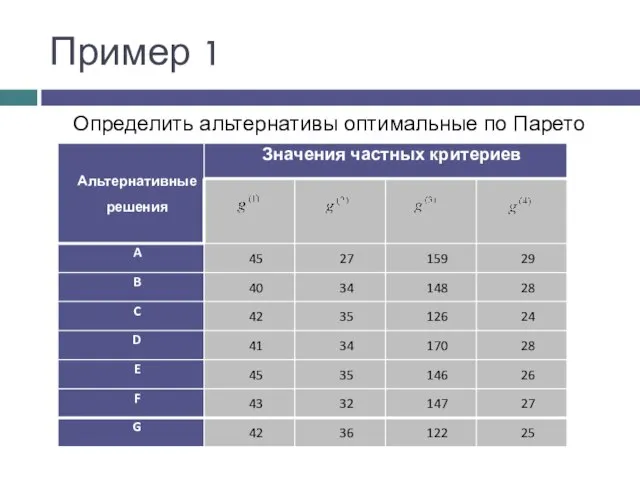
- 8. Пример 1 Определить альтернативы оптимальные по Парето
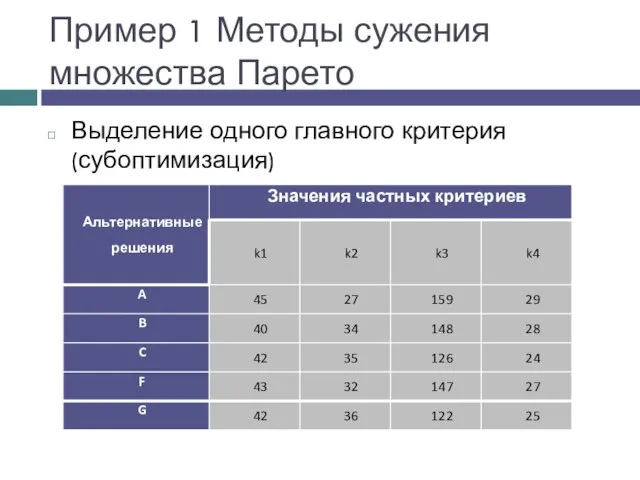
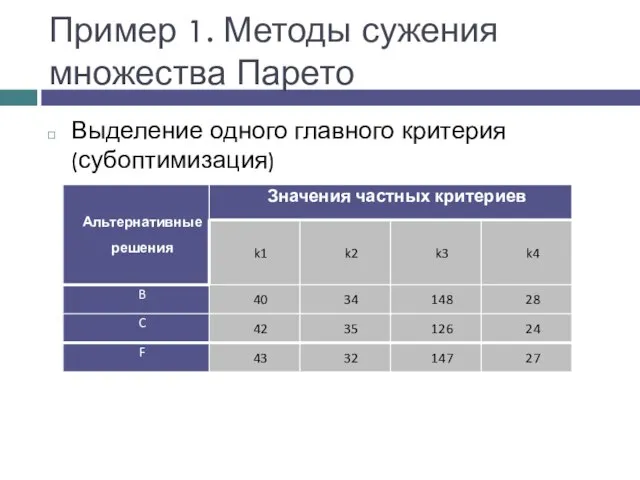
- 9. Пример 1 Методы сужения множества Парето Выделение одного главного критерия (субоптимизация)
- 10. Пример 1 Задача многокритериальной оптимизации будет преобразована к виду: ( ) → min при ограничениях ≤
- 11. Пример 1. Методы сужения множества Парето Выделение одного главного критерия (субоптимизация)
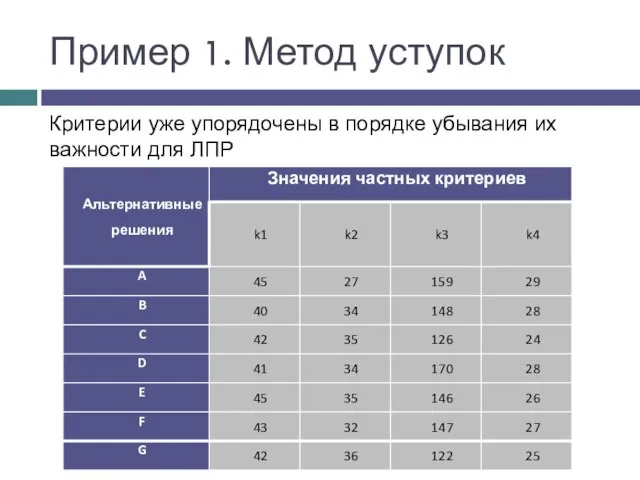
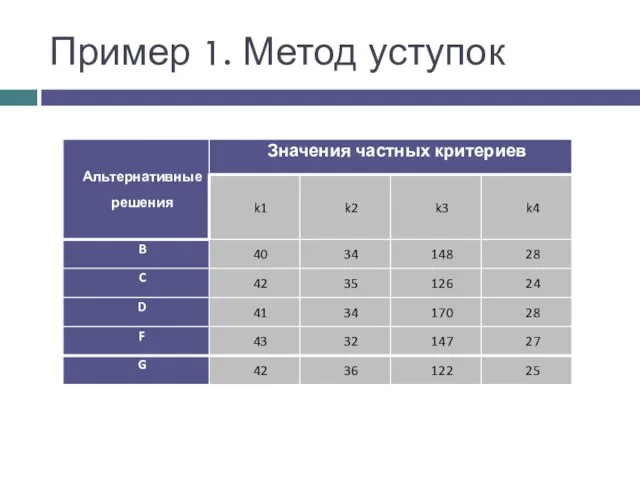
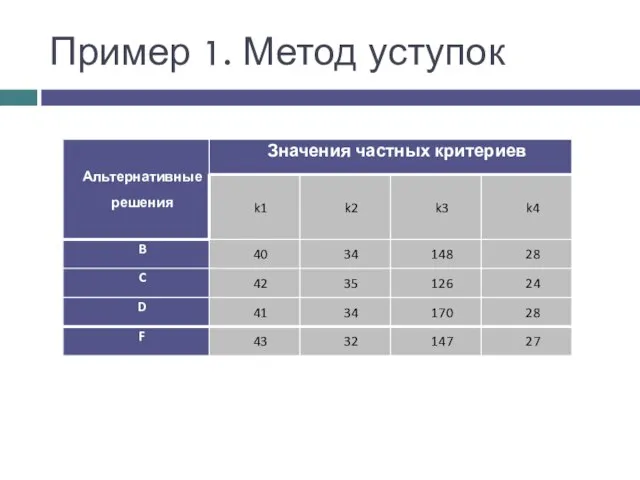
- 12. Пример 1. Метод уступок Критерии уже упорядочены в порядке убывания их важности для ЛПР
- 13. Пример 1. Метод уступок
- 14. Пример 1. Метод уступок
- 15. МНОГОКРИТЕРИАЛЬНОЕ ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ ОПРЕДЕЛЕННОСТИ a.s.grishchenko@gmail.com andrew.tgn@gmail.com Практические занятия
- 16. Метод замены векторного критерия скалярным критерием (линейная свертка) Метод линейной свертки заключается в том, что обобщённый
- 17. Метод замены векторного критерия скалярным критерием (линейная свертка) В случае максимизации критериев (чем больше показатель, тем
- 18. В случае минимизации критериев (чем меньше показатель, тем лучше) из максимального элемента столбца вычитают каждый элемент
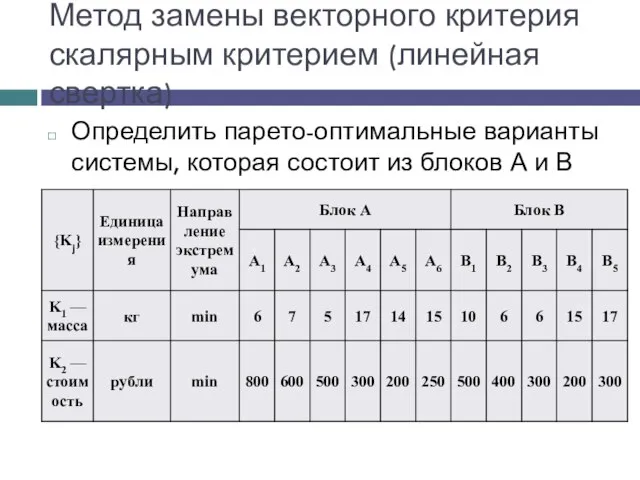
- 19. Определить парето-оптимальные варианты системы, которая состоит из блоков А и В Метод замены векторного критерия скалярным
- 20. Значения оптимальных вариантов отдельно по блокам Рассчитаем значения нормализованных критериев… Метод замены векторного критерия скалярным критерием
- 21. Значения нормализованных критериев Метод замены векторного критерия скалярным критерием (линейная свертка)
- 22. Допустим, что стоимость (К2) имеет вес 2, а масса (К1) – 1. Тогда вес критерия К1
- 24. Скачать презентацию














 Microsoft Access Мәліметтер қорын басқару жүйесі
Microsoft Access Мәліметтер қорын басқару жүйесі Презентация "Компьютерные презентации" - скачать презентации по Информатике
Презентация "Компьютерные презентации" - скачать презентации по Информатике Разработка сайта визитки для учебного заведения Филиала ФГБОУ ВО УдГУ в г.Губкинском
Разработка сайта визитки для учебного заведения Филиала ФГБОУ ВО УдГУ в г.Губкинском Управление проектами. Определения и концепции
Управление проектами. Определения и концепции GNU Эмулятор, вызов подпрограмм
GNU Эмулятор, вызов подпрограмм CSS Properties. The position property
CSS Properties. The position property Виды и классификация промышленных сетей
Виды и классификация промышленных сетей Знакомство с интерфейсом программы Кумир
Знакомство с интерфейсом программы Кумир Особенности операционных систем семейства UNIX
Особенности операционных систем семейства UNIX Поняття комп'ютерної публікації. Засоби створення публікації
Поняття комп'ютерної публікації. Засоби створення публікації Долговременная память
Долговременная память Создание и оформление реферата
Создание и оформление реферата Правила сетевого этикета
Правила сетевого этикета Процедурное программирование. Конструкция ветвления. Циклы. Массивы
Процедурное программирование. Конструкция ветвления. Циклы. Массивы Crypto
Crypto Процесс шифрования и дешифрования. Лекция №2 по технологии программирования
Процесс шифрования и дешифрования. Лекция №2 по технологии программирования Отечественные полнотекстовые электронные ресурсы для читателей ГПНТБ СО РАН
Отечественные полнотекстовые электронные ресурсы для читателей ГПНТБ СО РАН Мобильные сервисы в сетях 4G
Мобильные сервисы в сетях 4G Архитектура операционных систем
Архитектура операционных систем Всемирная паутина. Информация и информационные процессы
Всемирная паутина. Информация и информационные процессы Язык разметки гипертекста НТМL
Язык разметки гипертекста НТМL  Табличная форма представления информации
Табличная форма представления информации Sistēmas robežas un dekompozīcija
Sistēmas robežas un dekompozīcija Доэлектронная история вычислительной техники. (Глава 1)
Доэлектронная история вычислительной техники. (Глава 1) Економічна інформація і засоби її формалізованого опису
Економічна інформація і засоби її формалізованого опису Наиболее часто используемые форматы звуковых файлов
Наиболее часто используемые форматы звуковых файлов Память компьютера
Память компьютера Методы противодействия социальной инженерии в системе безопасности объекта
Методы противодействия социальной инженерии в системе безопасности объекта