Содержание
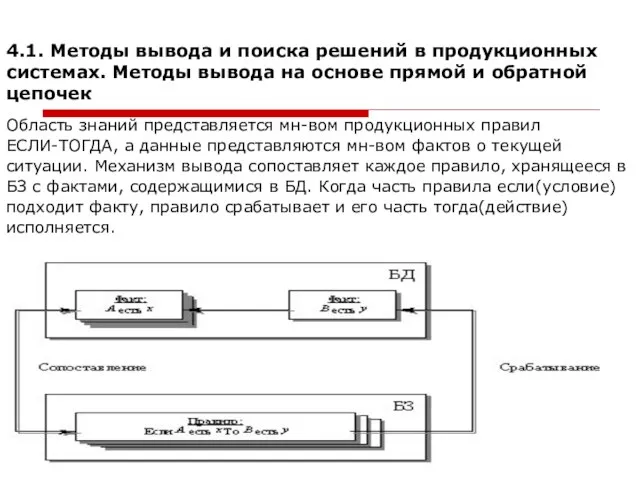
- 2. 4.1. Методы вывода и поиска решений в продукционных системах. Методы вывода на основе прямой и обратной
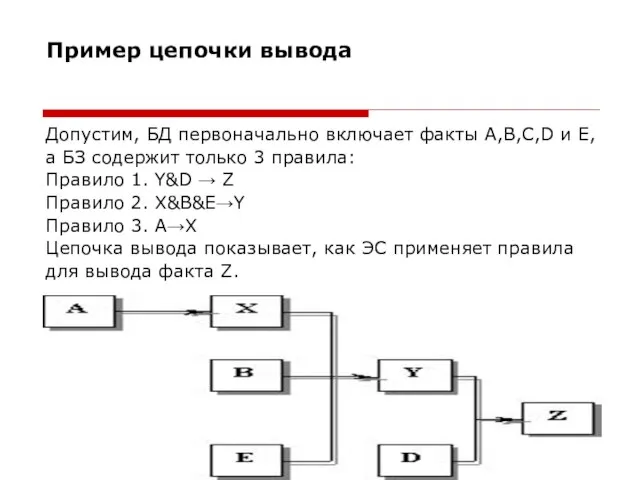
- 3. Пример цепочки вывода Допустим, БД первоначально включает факты А,В,С,D и Е, а БЗ содержит только 3
- 4. Целе-выводимые (действие-выводимые или консеквент-выводимые) продукционные системы Правило вида А&В&С→D может быть интерпретировано, как «Логическая конъюнкция А,
- 5. Пример продукционной системы с консеквент-выводимой архитектурой Дано: БД: АF Правило 4: В→С Правило 1: A&B&C→D Правило
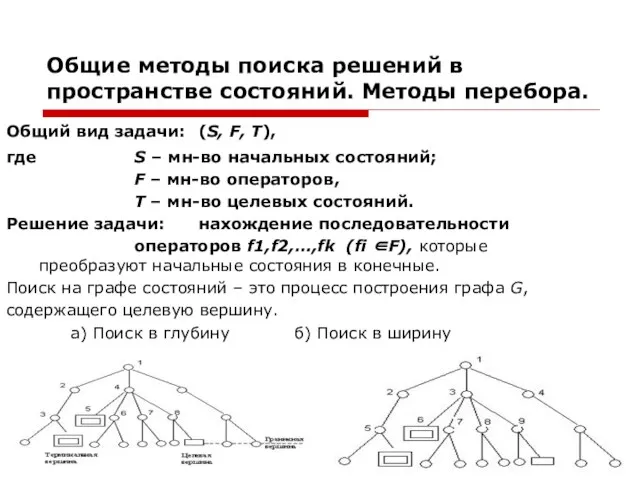
- 6. Общие методы поиска решений в пространстве состояний. Методы перебора. Общий вид задачи: (S, F, T), где
- 7. Эвристические методы поиска Используются при наличии некоторых эмпирических правил, которые позволяют сокращать объем вариантов решений. Открытие
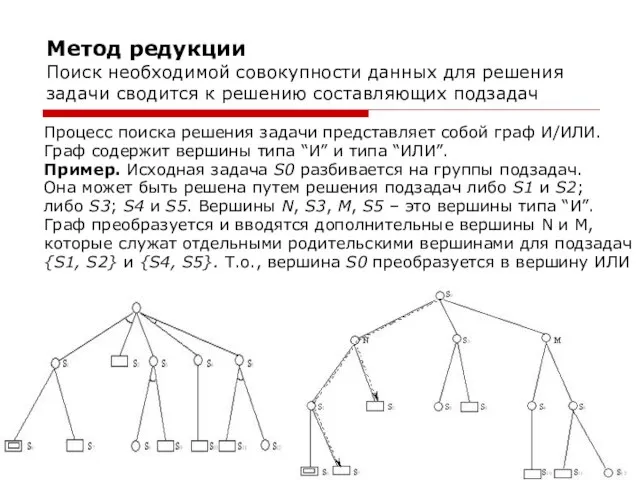
- 8. Метод редукции Поиск необходимой совокупности данных для решения задачи сводится к решению составляющих подзадач Процесс поиска
- 9. Методы поиска решений в больших пространствах состояний Метод порождения и проверки Генератор, настроенный на проблемную область,
- 10. 4.2. Выводы на фреймах и в семантических сетях 4.2.1. Вывод на фреймах Структура данных фрейма Имя
- 11. Вывод во фреймовой системе 3 основных процесса, происходящие во фреймовых системах: Создание экземпляра фрейма Активация фреймов
- 12. 4.2.2. Вывод в семантических сетях. Структурирование знаний в семантической сети Использование предикатов отношений двух типов: *является
- 13. Процедурные семантические сети Процедурные семантические сети используются в целях введения единой семантики в семантической сети. Сеть
- 14. Вывод в семантических сетях Особенностью и недостатком семантической сети является целостность системы, не позволяющей разделить БЗ
- 15. 4.3. Дедуктивные методы вывода Вывод на предикатах Основные формы логического вывода: Индукция (лат. наведение) Дедукция (лат.
- 16. Законы эквивалентных преобразований 4.1 4.2 4.3а P∨ (Q∧H)=(P∨Q) ∧ (P∨H) 4.3б P ∧ (Q∨H)=(P∧Q) ∨ (P∧H)
- 17. Правила вывода в логике высказываний Правило подстановки. Пусть Р – ППФ, содержащая атомарную ф-лу Х. Тогда
- 18. Пример использования правил вывода Пусть в некоторой ПО справедливы следующие утверждения: 1. f1: если скорость движения
- 19. f1 : S→P, F2:P→U; F3:S; F4:U. Покажем, что F4 истинно, как только F1∧ F2∧F3 истинно. Преобразуем
- 20. Типы символов, использующиеся для построения атомарных формул : индивидные символы (имена объектов), или константы (строчные буквы
- 21. Основные правила в логике предикатов Правила обобщения (правило связывания квантором общности). Пусть Q — ф-ла, не
- 22. Законы, содержащие кванторы 4.10а xP(x)∨Q= x{P(x)∨Q}, 4.10б xP(x)∧ Q= x{P(x) ∧Q}, 4.11а ∀xP(x)=¬∃x¬P(x), 4.11б ∃xP(x)=¬ ∀x¬P(x),
- 23. Процедура стандартизации - преобразования формул в предложения (необходима для использования метода Эрбрана и метода резолюций) Предложение
- 24. Метод Эрбрана Применяется процедура поиска опровержения, т.е. вместо доказательства общезначимости ф-лы доказывается, что опровержение ф-лы противоречиво.
- 25. Метод Эрбрана (продолжение) Pn(t1,..., tn) - n-местная атомарная формула в S. Эрбрановская база для мн-ва S
- 26. Метод резолюций Цель метода- проверка невыполнимости мн-ва дизъюнктов. Метод резолюции является правилом вывода, при использовании которого
- 27. Метод резолюций (продолжение) Если имеются два однолитерных дизъюнкта, образующих контрарную пару, то их резольвента есть пустой
- 28. 4.4. Вывод в условиях неопределенности Неопределенность Любая предметная область реального мира содержит неточные знания и нужно
- 29. 4.4.1. Вероятностный вывод Вероятностный подход Основные положения байесовского метода и правило Байеса Условная вер-ть р(А|B)– вер-ть
- 30. Основные положения байесовского метода и правило Байеса (продолжение) Пусть событие А зависит не просто от события
- 31. Байесовский вывод Пусть правила БЗ имеют вид: Если Н истинно,тогда С истинно {с вер. р} Подставив
- 32. Байесовский вывод. Пример Пусть при наличии 3х условно независимых свидетельства С1, С2 и С3, Эксперт создает
- 33. Байесовский вывод. Пример (продолжение) Предположим теперь, что мы наблюдаем свидетельство С1. Апостериорные вер-ти рассчитываются по ур-ю
- 34. Вывод на основе теории Демпстера-Шафера Проблемами байесовского подхода являются: * необходимость заранее устанавливать априорные вер-ти каждого
- 35. 4.4.2. Вывод на основе теории уверенности (ТУ) Коэффициент уверенности (КУ) и доверие Неопределенность представляется как степень
- 36. Объединение коэффициентов уверенности Наиболее приемлемым способом объединения КУ является подход, используемый в EMYCIN. При этом подходе
- 37. Объединение КУ (продолжение) II. Объединение двух и более правил. Если система, основана на знаниях с несколькими
- 38. 4.4.3. Нечеткая логика и приближенные рассуждения Истинность высказывания в нечеткозначной логике опр-ся значениями типа: истинно, ложно,
- 39. Приближенные рассуждения (продолжение) Пусть А-нечеткое подмн-во области рассуждений U и пусть B - нечеткое подмн-во другой
- 40. Приближенные рассуждения (продолжение) Чтобы обобщить понятие материальной импликации на нечеткие мн-ва, предположим, что U и V
- 41. Приближенные рассуждения Иллюстрация 4.40 и 4.41 Пусть, U=V=1+2+3 В=большой=0,4/2+1/3 А=малый=1/1+0,4/2 С=не большой=1/1+0,6/2 Тогда Если А, Тогда
- 42. Композиционное правило вывода (КПВ) Пусть U и V – 2 универсальных мн-ва с базовыми пер-ми u
- 43. Композиционное правило вывода. Иллюстрация U=V=1+2+3+4 A=малый=1/1+0.6/2+0./3 F= примерно равны=1/(1,1)+1/(2,2)+1/(3,3)+ 1/(4,4)+0,5/((1,2)+(2,1)+(2,3)+(3,2)+(3,4)+(4,3)). Т.е., А-унарное нечеткое отношение в U,
- 44. Напоминание Лингвистической называют пер-ую, если ее значениями являются слова или фразы естественного языка. При этом лингвистическая
- 45. Применение приближенных рассуждений и композиционного правила вывода (на примере управления технологической установкой) С – сырье, tc
- 46. Продолжение примера Для каждого терма из терм-множеств строится нечеткое мн-во М со своим носителем, определенное на
- 47. Напоминание Как известно, нечеткое бинарное отношение R есть подмн-во декартового произведения X × Y: Далее построенные
- 49. Скачать презентацию










































 Yappy. Что это за приложение?
Yappy. Что это за приложение? История развития информационной технологии
История развития информационной технологии  Activity diagram в контексте языка UML
Activity diagram в контексте языка UML Проектирование и разработка информационной системы Швейная фабрика
Проектирование и разработка информационной системы Швейная фабрика Приложении ЛесЕГАИС.mobile
Приложении ЛесЕГАИС.mobile Алгоритм действий
Алгоритм действий Разработка модели специалиста по защите информации
Разработка модели специалиста по защите информации Защита информации
Защита информации Устройства ввода и вывода информации. 8 класс
Устройства ввода и вывода информации. 8 класс Действия с информацией. Хранение информации
Действия с информацией. Хранение информации Инструкция по заполнению отчета школьного этапа
Инструкция по заполнению отчета школьного этапа Выполнение курсовой работы по дисциплине «Базы данных»
Выполнение курсовой работы по дисциплине «Базы данных» Ролик Мои правила безопасного поведения в сети
Ролик Мои правила безопасного поведения в сети Проектирование и администрирование компьютерной сети малого офиса
Проектирование и администрирование компьютерной сети малого офиса Сетевая криминалистика
Сетевая криминалистика СВОБОДНОЕ ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ Исследовательская работа
СВОБОДНОЕ ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ Исследовательская работа Базы данных Института научной информации по общественным наукам ИНИОН РАН
Базы данных Института научной информации по общественным наукам ИНИОН РАН Внеклассное мероприятие. Викторина "Информатика и логика"
Внеклассное мероприятие. Викторина "Информатика и логика" Специфика работы пресс-центра отряда
Специфика работы пресс-центра отряда Архитектура систем баз данных
Архитектура систем баз данных Профессия программист
Профессия программист Работа с графическими объектами в текстовом реакторе
Работа с графическими объектами в текстовом реакторе Информационные технологии в процессе социально-профессиональной адаптации обучающихся по программам профессионального обучения
Информационные технологии в процессе социально-профессиональной адаптации обучающихся по программам профессионального обучения Конфуций. Инжиниринг. Великий Же
Конфуций. Инжиниринг. Великий Же Поиск оптимального решения ЗЛП. Лекция (фрагмент)
Поиск оптимального решения ЗЛП. Лекция (фрагмент) Использование стека для вычисления выражений
Использование стека для вычисления выражений Предмет методики обучения информатике
Предмет методики обучения информатике Глобальная переменная $_SERVER
Глобальная переменная $_SERVER