Содержание
- 2. 2.4. Двойственная задача и ее решение. Целочисленное программирование
- 3. Каждой задаче ЛП можно определенным образом поставить в соответствие некоторую другую задачу ЛП, называемую сопряженной или
- 4. 1) в одной задаче ищут максимум целевой функции, в другой минимум; 2) обе задачи являются стандартными
- 5. Такие задачи решаются методами целочисленного программирования. Общая постановка задачи линейного программирования дополняется требованием о том, чтобы
- 6. 2.5. Симплекс-метод решения задач ЛП
- 7. Графический способ решения задачи ЛП показывает, что оптимальное решение этой задачи всегда ассоциируется с угловой точкой
- 8. ? Симплекс – это выпуклый многоугольник в n-мерном пространстве с n+1 вершинами, не лежащими в одной
- 9. Переход от геометрического способа решения задачи ЛП к симплекс-методу лежит через алгебраическое описание крайних точек пространства
- 11. Требования к ограничениям: 1. Все ограничения (включая ограничения неотрицательности переменных) преобразуются в равенства с неотрицательной правой
- 12. Преобразование неравенств в равенства Неравенства любого типа (со знаками неравенств «≤» или «≥») можно преобразовать в
- 13. Пример 2.4. Преобразовать следующую задачу ЛП в стандартную форму: при выполнении следующих условий:
- 14. Действия:
- 15. Получаем: при выполнении следующих условий:
- 16. 2.5.2. Основы симплекс-метода
- 17. Рассмотрим общую ЗЛП с m ограничениями и n переменными, записанную в стандартной (канонической) форме: (2.1)
- 18. Как правило, число уравнений задачи меньше числа переменных (т. е. m Задача состоит в том, чтобы
- 19. Получение одного из базисных решений основано на методе решения систем линейных уравнений Гаусса–Жордана. Основная идея: сведение
- 20. При использовании первых m переменных такая система имеет следующий вид: (2.2)
- 21. При записи системы в каноническом виде все ее решения можно получить, присваивая независимым переменным произвольные значения
- 22. ? Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных что эквивалентно
- 23. Поэтому ЗЛП можно решать посредством перебора конечного числа угловых точек допустимого множества S , сравнивая значения
- 24. СМ разработал американский ученый Дж. Данциг в 1947 г. Идея симплекс-метода (СМ) состоит в направленном переборе
- 25. Гарантии результативности СМ обеспечиваются следующей теоремой. Теорема (о конечности алгоритма симплекс-метода). Если существует оптимальное решение ЗЛП,
- 26. 2.5.3. Вычислительный алгоритм симплекс-метода
- 27. Рассмотрим работу алгоритма на примере компании Mikks. Математическая модель:
- 28. Математическая модель: В стандартной форме:
- 29. В стандартной форме: Замечание. Если целевую функцию необходимо максимизировать, то предварительно нужно умножить ее на (–1)
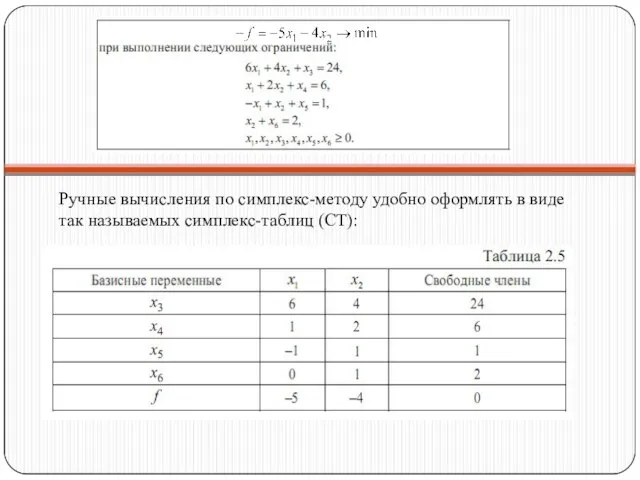
- 30. Ручные вычисления по симплекс-методу удобно оформлять в виде так называемых симплекс-таблиц (СТ):
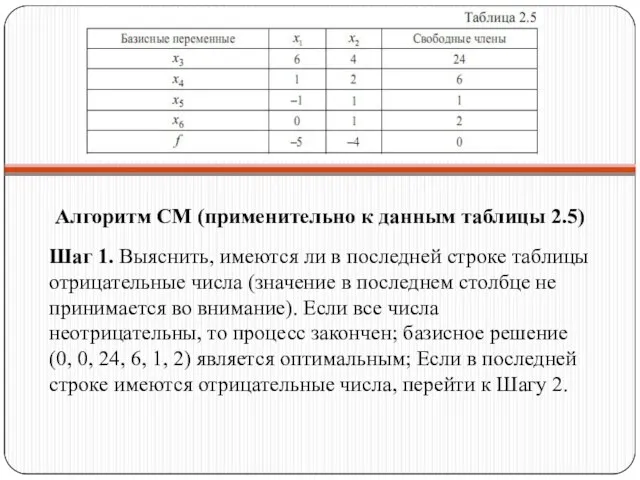
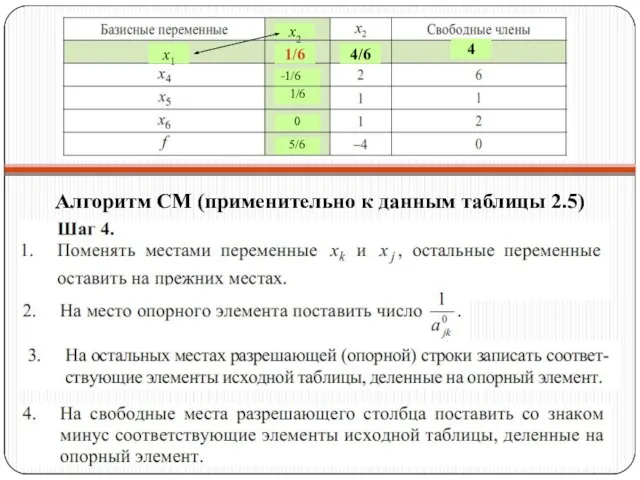
- 31. Алгоритм СМ (применительно к данным таблицы 2.5) Шаг 1. Выяснить, имеются ли в последней строке таблицы
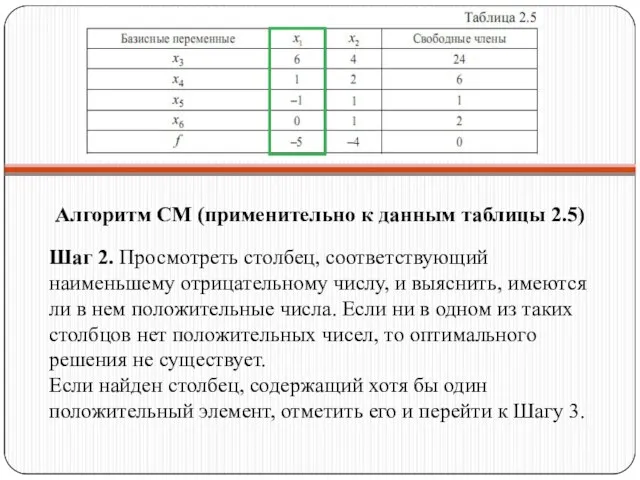
- 32. Алгоритм СМ (применительно к данным таблицы 2.5) Шаг 2. Просмотреть столбец, соответствующий наименьшему отрицательному числу, и
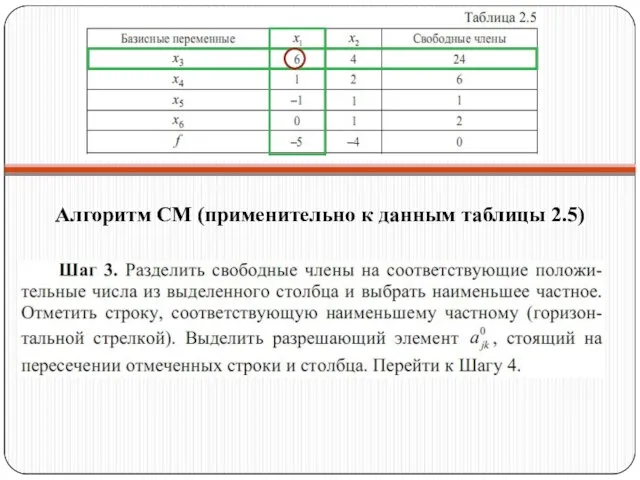
- 33. Алгоритм СМ (применительно к данным таблицы 2.5)
- 34. Алгоритм СМ (применительно к данным таблицы 2.5) x1 x2 1/6 4/6 4 -1/6 1/6 0 5/6
- 35. Алгоритм СМ (применительно к данным таблицы 2.5) x1 x2 1/6 4/6 4 -1/6 1/6 0 5/6
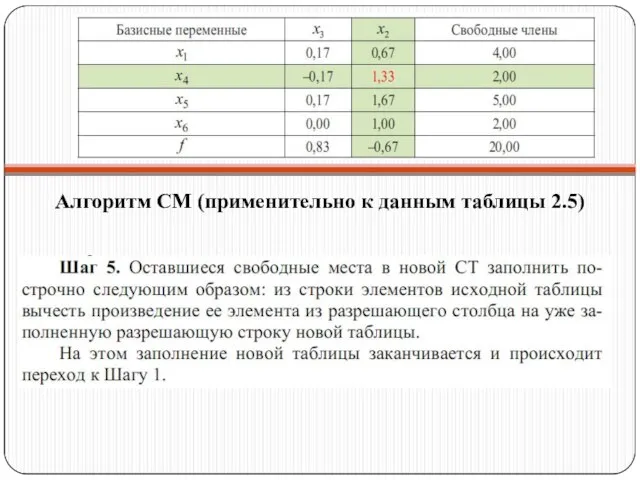
- 36. Алгоритм СМ (применительно к данным таблицы 2.5)
- 38. Спасибо за внимание!
- 40. Скачать презентацию































 Электронная почта
Электронная почта Презентация по дисциплине Аппаратные средства ИС Тема: Мобильная связь ( поколение мобильных телефонов) Подготовила: Рузиева
Презентация по дисциплине Аппаратные средства ИС Тема: Мобильная связь ( поколение мобильных телефонов) Подготовила: Рузиева Методические рекомендации к подготовке отчета в виде мультимедийной презентации
Методические рекомендации к подготовке отчета в виде мультимедийной презентации Правила техники безопасности в походе
Правила техники безопасности в походе All about internet
All about internet Математические методы в программировании (ММвП)
Математические методы в программировании (ММвП) Мастер-класс Как создать буктрейлер?
Мастер-класс Как создать буктрейлер? Тренинг. Бизнес с Китаем в сети интернет. (Занятие 2)
Тренинг. Бизнес с Китаем в сети интернет. (Занятие 2) Информация - это …
Информация - это … ScratchJR 2. Урок #2
ScratchJR 2. Урок #2 Инструкция по работе в электронной образовательной среде
Инструкция по работе в электронной образовательной среде Microsoft Word Формулы
Microsoft Word Формулы «Как влияет компьютер на здоровье школьника?» Выполнил: Кретов Ярослав, ученик 4 класса МОУ СОШ № 2 г. Ртищево Саратовской области.
«Как влияет компьютер на здоровье школьника?» Выполнил: Кретов Ярослав, ученик 4 класса МОУ СОШ № 2 г. Ртищево Саратовской области.  Растровые изображения на экране монитора. Палитры цветов в системах цветопередачи
Растровые изображения на экране монитора. Палитры цветов в системах цветопередачи Матрицы (многомерные массивы)
Матрицы (многомерные массивы) Презентация на тему: «Налаживаем взаимодействие между компьютерами: настройка IP-адресации и маршрутизации.» Выполнила ученица 10
Презентация на тему: «Налаживаем взаимодействие между компьютерами: настройка IP-адресации и маршрутизации.» Выполнила ученица 10  Локальные сети
Локальные сети Компьютерная графика. Растровые и векторные изображения
Компьютерная графика. Растровые и векторные изображения Компьютерные сети
Компьютерные сети Интернет - мошенничество вчера, сегодня, завтра. Взаимодействие компетентных организаций и регистраторов доменных имен
Интернет - мошенничество вчера, сегодня, завтра. Взаимодействие компетентных организаций и регистраторов доменных имен Программная инженерия
Программная инженерия Строки
Строки Виртуальное общение подростков
Виртуальное общение подростков Логические задачи
Логические задачи Системы перевода и распознования текстов
Системы перевода и распознования текстов Базис и Мкм. 10 первых задач
Базис и Мкм. 10 первых задач Уроки по Spike Prime. Циклы
Уроки по Spike Prime. Циклы pravila_web-saita
pravila_web-saita