Содержание
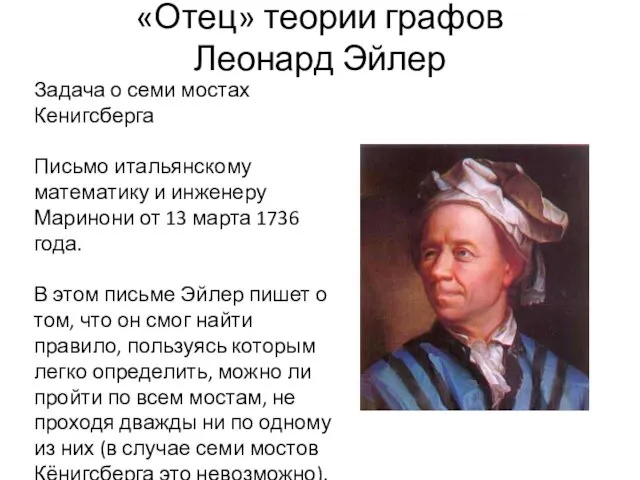
- 2. «Отец» теории графов Леонард Эйлер Задача о семи мостах Кенигсберга Письмо итальянскому математику и инженеру Маринони
- 3. Мосты Кенигсберга
- 4. Если дана геометрическая фигура, как начертить ее на бумаге одним росчерком пера, не проводя дважды ни
- 5. Прикладные задачи 1847 год Физик Густав Роберт Кирхгоф Теория графов для исследования электрических цепей Множество фундаментальных
- 6. Прикладные задачи 1857 год Математик Артур Кэли Задачи органической химии
- 7. Перечислить число предельных углеводородов с данным числом n атомов углерода На языке графов: найти число всех
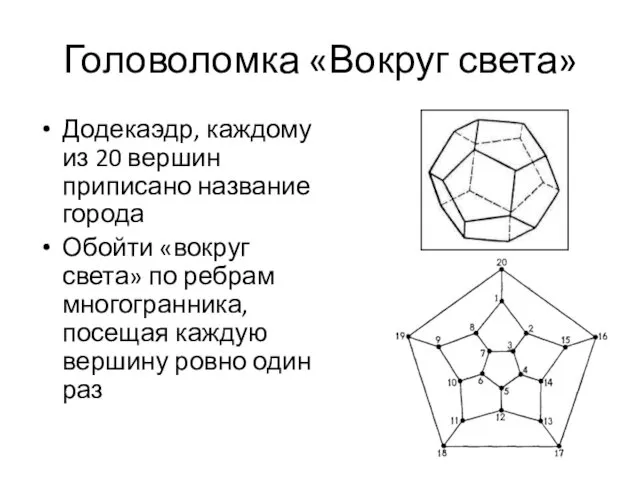
- 8. Головоломки 1859 год Сэр Уи́льям Ро́уэн Га́мильтон Головоломка «Вокруг света»
- 9. Головоломка «Вокруг света» Додекаэдр, каждому из 20 вершин приписано название города Обойти «вокруг света» по ребрам
- 11. Задача коммивояжера (англ. Travelling salesman problem, TSP) — задача, в которой коммивояжер должен посетить N городов,
- 12. Задача о домиках и колодцах Три поссорившихся соседа имеют три общих колодца. Можно ли провести непересекающиеся
- 13. Полный двудольный граф К3,3 Доказано, что данный граф непланарен, то есть задача о домиках и колодцах
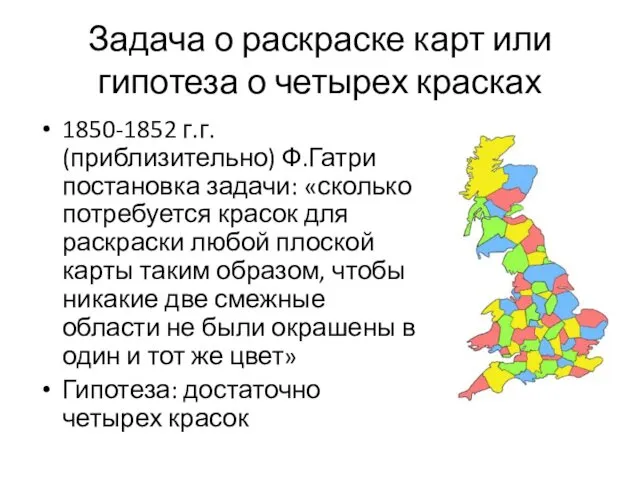
- 14. Задача о раскраске карт или гипотеза о четырех красках 1850-1852 г.г. (приблизительно) Ф.Гатри постановка задачи: «сколько
- 15. Задача о раскраске карт или гипотеза о четырех красках 1879 г. британский математик Альфред Брей Кемпе
- 16. 1975 г. известный популяризатор науки и многолетний ведущий раздела «Математические игры» журнала «Scientific American» Мартин Гарднер
- 17. 1976 г. два математика из Иллинойского университета, Вольфганг Хакен и Кеннет Аппель, предложили новый метод, перевернувший
- 18. Примеры Вершины – города, ребра - дороги между ними Вершины – города, ребра – наличие авиарейса
- 19. Теория графов в игре престолов https://habrahabr.ru/post/302936/ Граф социальной активности Вершинам соответствуют персонажи; размер вершины зависит от
- 21. Общие сведения о графе Граф неориентированный. Вершин (персонажей): 1105 Рёбер (диалогов): 3505 5 книг, почти 2
- 22. Алгоритмы на графе Подсчет степеней вершин – самые многосвязные персонажи Диаметр графа (расстояние между наиболее удаленными
- 23. Распределение длин путей
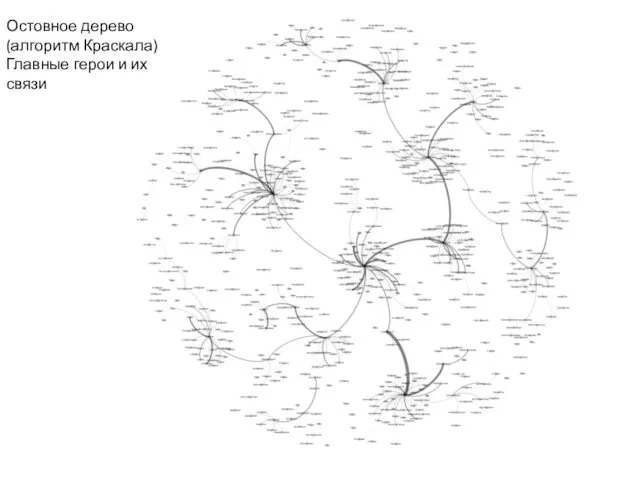
- 24. Остовное дерево (алгоритм Краскала) Главные герои и их связи
- 25. Математическая модель интернета – веб-граф (А.Райгородский) http://elementy.ru/nauchno-populyarnaya_biblioteka/431792/Matematicheskie_modeli_interneta Вершинами этого графа будут сайты, и между двумя вершинами
- 26. Свойства веб-графа Диаметр веб-графа равен 6 (закон шести рукопожатий) Веб-граф является достаточно разреженным: если вершин у
- 27. Алгоритм PageRank PageRank был представлен и опубликован Сергеем Брином (Sergey Brin) и Ларри Пейджем (Larry Page)
- 28. Алгоритм PageRank и футбольные команды https://geektimes.ru/post/247244/ Вершины графа – команды, ребра – матчи. Вес ребра зависит
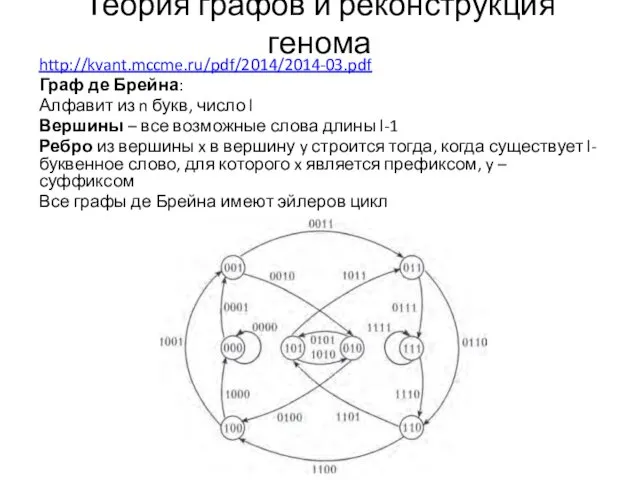
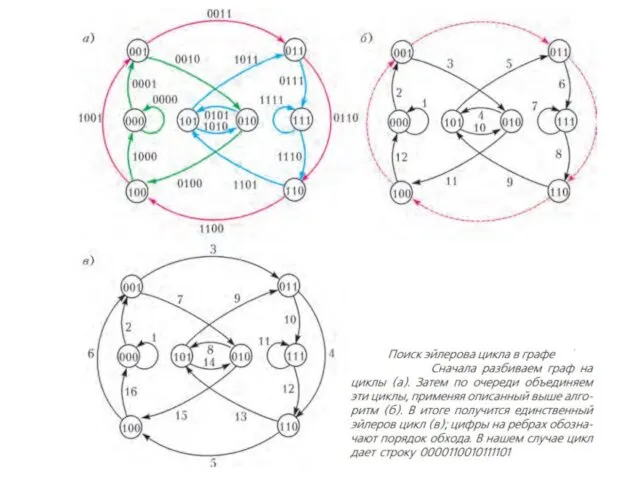
- 29. Теория графов и реконструкция генома http://kvant.mccme.ru/pdf/2014/2014-03.pdf Граф де Брейна: Алфавит из n букв, число l Вершины
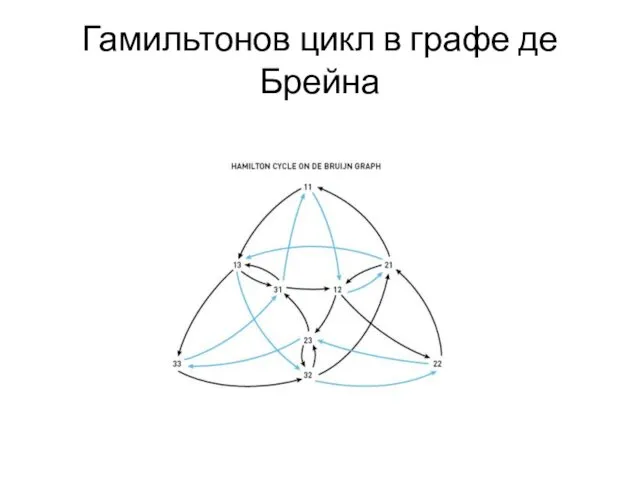
- 31. Гамильтонов цикл в графе де Брейна
- 32. Граф дорог – это цифровая векторная карта, состоящая из топологически связанных дуг и узлов, местоположение и
- 33. Яндекс – школа данных Задача о предсказании пробок на небольшой промежуток времени вперед http://imat2010.yandex.ru/ Данные Граф
- 34. Метод деревьев решений (decision trees) является одним из наиболее популярных методов решения задач классификации и прогнозирования.
- 35. Выдача кредита
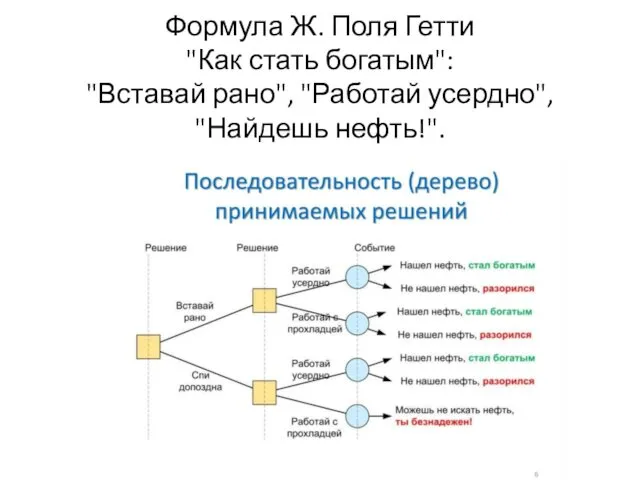
- 36. Формула Ж. Поля Гетти "Как стать богатым": "Вставай рано", "Работай усердно", "Найдешь нефть!".
- 39. Анализ больших данных. Поиск сообществ в графах. Задачи кластеризации Выделение сообществ (кластеров) разных объектов: пользователей, сайтов,
- 40. ПОИСК СООБЩЕСТВ В НЕОРИЕНТИРОВАННЫХ ГРАФАХ (ГРАФ ДОМЕНОВ РУНЕТА - 1285) https://habrahabr.ru/company/dca/blog/265077/ Вершины – домены Рёбра —
- 42. Скачать презентацию































 Uploading documents
Uploading documents Компьютерные вирусы
Компьютерные вирусы Массивы. Описание массивов
Массивы. Описание массивов Базовые типы данных языков программирования высокого уровня. Лекция 3
Базовые типы данных языков программирования высокого уровня. Лекция 3 Действия с информацией
Действия с информацией Introduction to PL/SQL
Introduction to PL/SQL Информация как важный ресурс общества
Информация как важный ресурс общества Языки программирования
Языки программирования Сетевые информационные технологии
Сетевые информационные технологии Наука наше будущее
Наука наше будущее Язык программирования C# 8.0 модуль 1
Язык программирования C# 8.0 модуль 1 Текстовые документы и технологии их создания
Текстовые документы и технологии их создания Xüsusi karantin rejiminin tətbiqi zamanı i̇cazələrin alınması və monitorinqi sistemi
Xüsusi karantin rejiminin tətbiqi zamanı i̇cazələrin alınması və monitorinqi sistemi Центр інформаційних технологій УДППЗ Укрпошта. Стан автоматизації виробничих та бізнес-процесів та управління підприємством
Центр інформаційних технологій УДППЗ Укрпошта. Стан автоматизації виробничих та бізнес-процесів та управління підприємством Magicdom
Magicdom BIM на этапе строительства
BIM на этапе строительства Аттестационная работа. Программа внеурочной деятельности Lego-конструирование
Аттестационная работа. Программа внеурочной деятельности Lego-конструирование Аттестационная работа. Значение включения в программу по информатике материала, освоенного в рамках курса
Аттестационная работа. Значение включения в программу по информатике материала, освоенного в рамках курса Как вести себя на улице 1 класс
Как вести себя на улице 1 класс Презентация "ИНФОРМАЦИЯ И ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ" - скачать презентации по Информатике__
Презентация "ИНФОРМАЦИЯ И ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ" - скачать презентации по Информатике__ Презентация выступления (Тема 31)
Презентация выступления (Тема 31) Работа с Microsoft Visio 2010
Работа с Microsoft Visio 2010 Презентация "Подготовка к контрольной работе (4 класс)" - скачать презентации по Информатике
Презентация "Подготовка к контрольной работе (4 класс)" - скачать презентации по Информатике Контекст и дескриптор процесса
Контекст и дескриптор процесса Растровая и векторная графика
Растровая и векторная графика Функціональна методологія IDEF0. Основні положення
Функціональна методологія IDEF0. Основні положення Шифрование и дешифрование осмысленного текста с ключом
Шифрование и дешифрование осмысленного текста с ключом Встроенный SQL. Хранимые процедуры. (Лекция 8)
Встроенный SQL. Хранимые процедуры. (Лекция 8)