Кавальери Бонавентуре

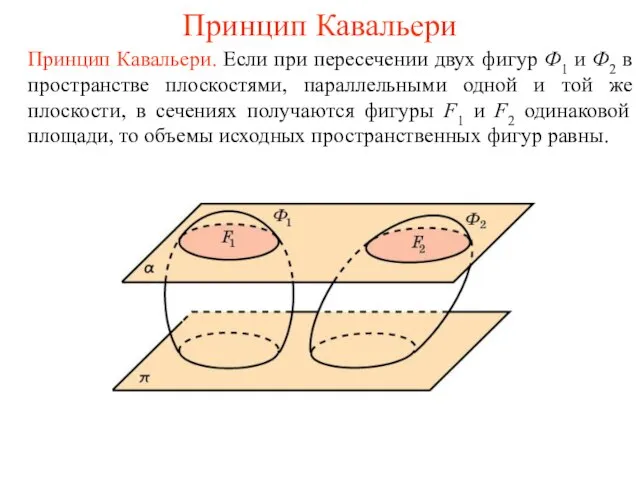
Принцип Кавальери

Принцип Кавальери. Если при пересечении двух фигур Ф1 и Ф2

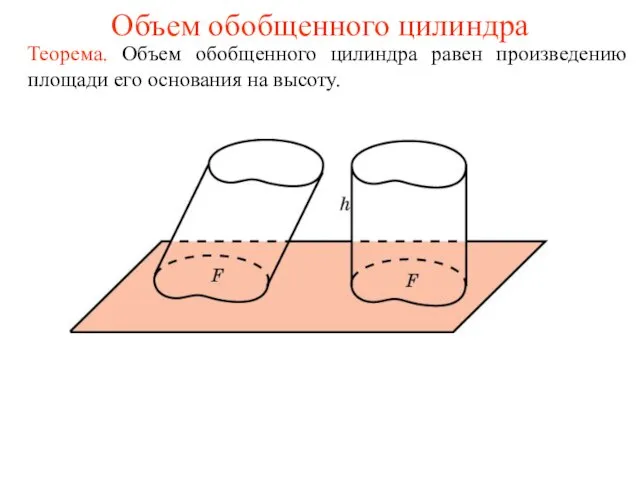
Объем обобщенного цилиндра

Теорема. Объем обобщенного цилиндра равен произведению площади его основания

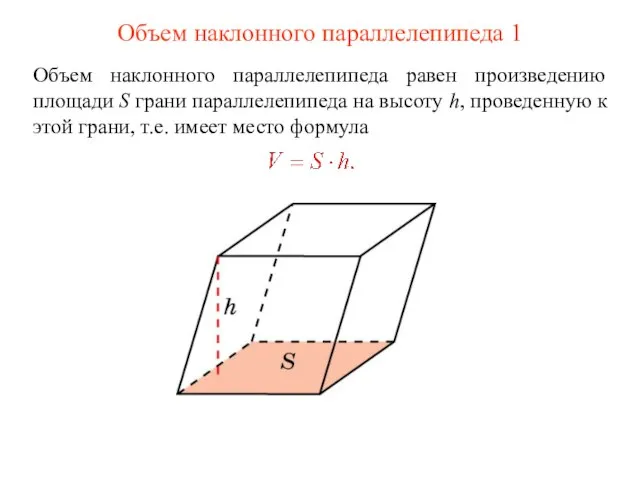
Объем наклонного параллелепипеда 1

Объем наклонного параллелепипеда равен произведению площади S грани

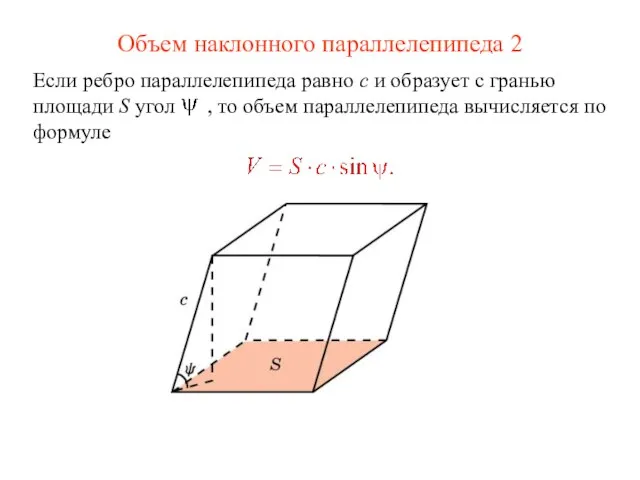
Объем наклонного параллелепипеда 2

Если ребро параллелепипеда равно c и образует с

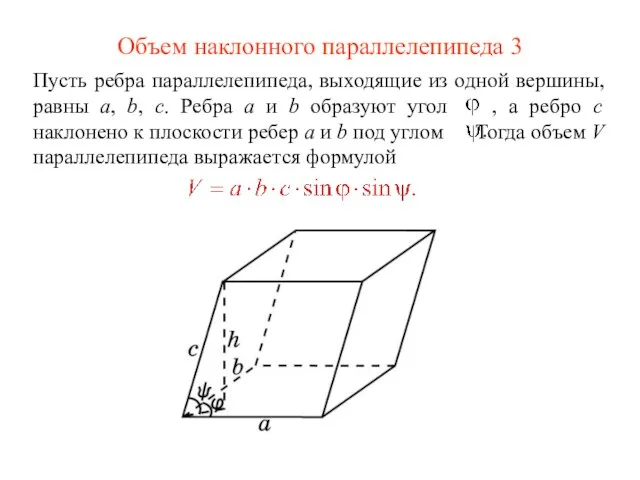
Объем наклонного параллелепипеда 3

Пусть ребра параллелепипеда, выходящие из одной вершины, равны

Упражнение 1

Две противоположные грани параллелепипеда – квадраты со стороной 1. Соединяющее

Упражнение 2

Гранью параллелепипеда является ромб со стороной 1 и острым углом

Упражнение 3

Три грани параллелепипеда, имеющие общую вершину, являются ромбами со сторонами

Упражнение 4

В параллелепипеде две грани имеют площади S1 и S2, их

Упражнение 5

В параллелепипеде две грани являются прямоугольниками с площадями 20 см2

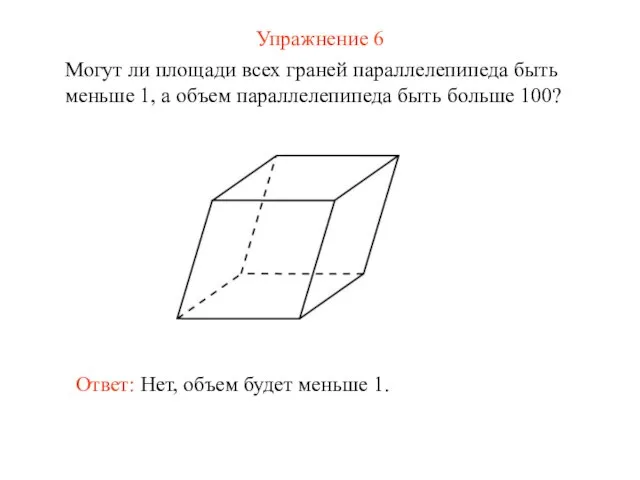
Упражнение 6

Могут ли площади всех граней параллелепипеда быть меньше 1, а

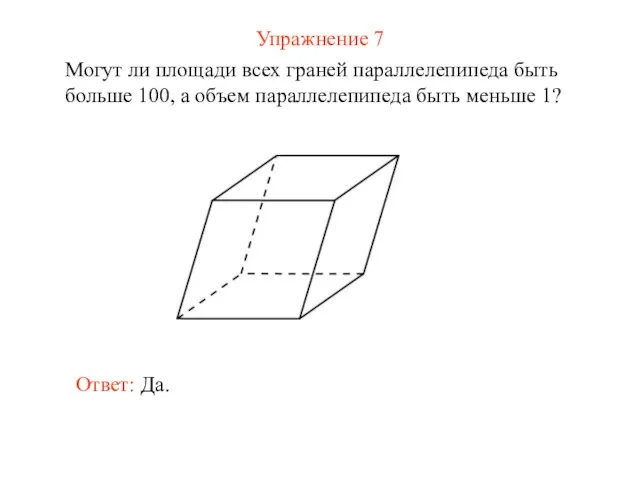
Упражнение 7

Могут ли площади всех граней параллелепипеда быть больше 100, а

Упражнение 8*

Какой наибольший объем может иметь параллелепипед, сумма длин ребер которого,

Упражнение 9*

В пространстве даны три параллелепипеда. Как провести плоскость, чтобы она

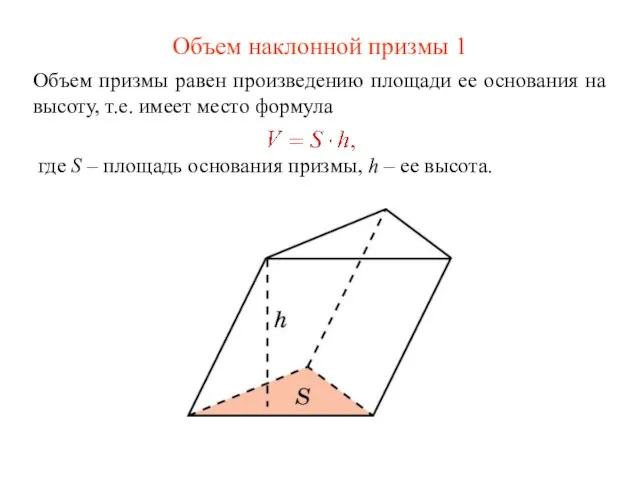
Объем наклонной призмы 1

Объем призмы равен произведению площади ее основания на

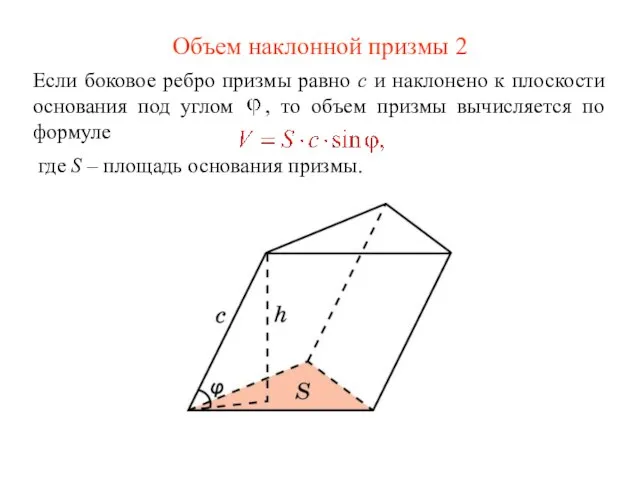
Объем наклонной призмы 2

Если боковое ребро призмы равно c и наклонено

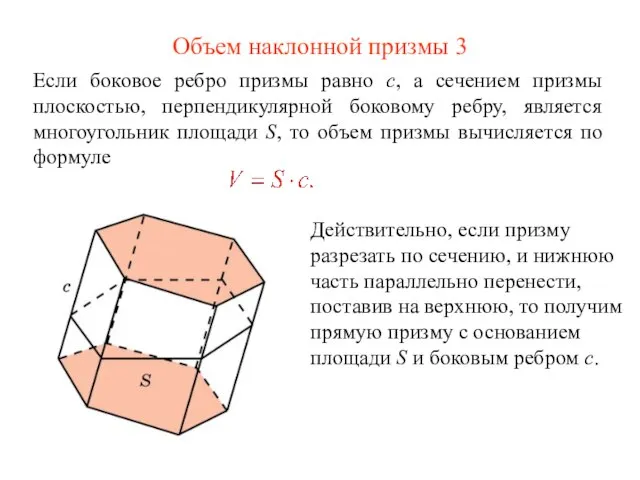
Объем наклонной призмы 3

Если боковое ребро призмы равно c, а сечением

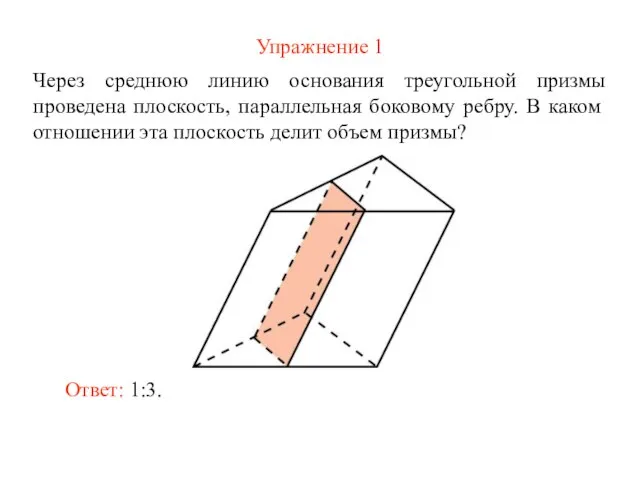
Упражнение 1

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому

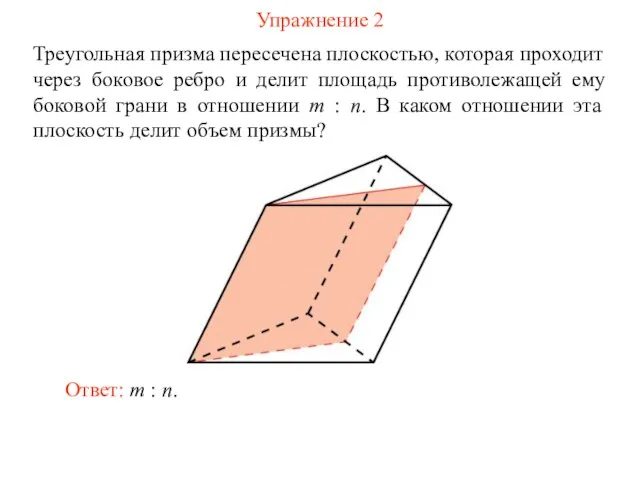
Упражнение 2

Треугольная призма пересечена плоскостью, которая проходит через боковое ребро и

Упражнение 3

В наклонной треугольной призме площадь одной из боковых граней равна

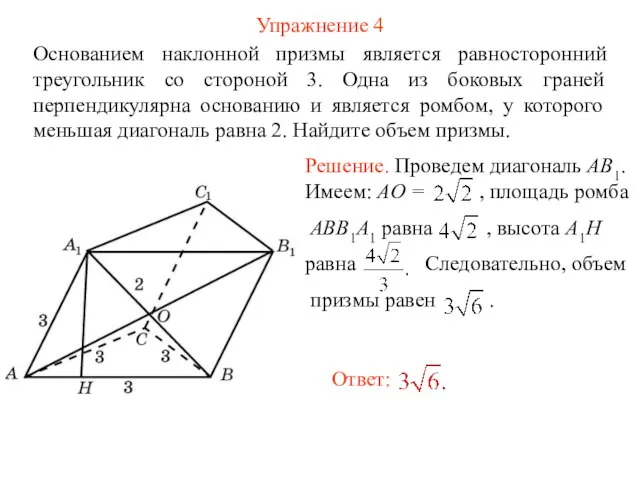
Упражнение 4

Основанием наклонной призмы является равносторонний треугольник со стороной 3. Одна

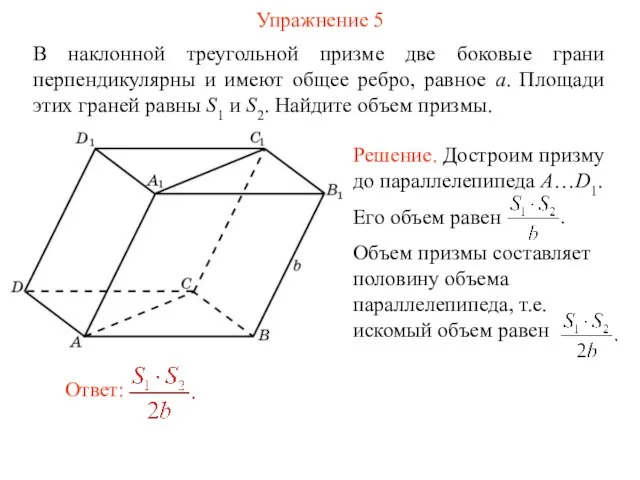
Упражнение 5

В наклонной треугольной призме две боковые грани перпендикулярны и имеют

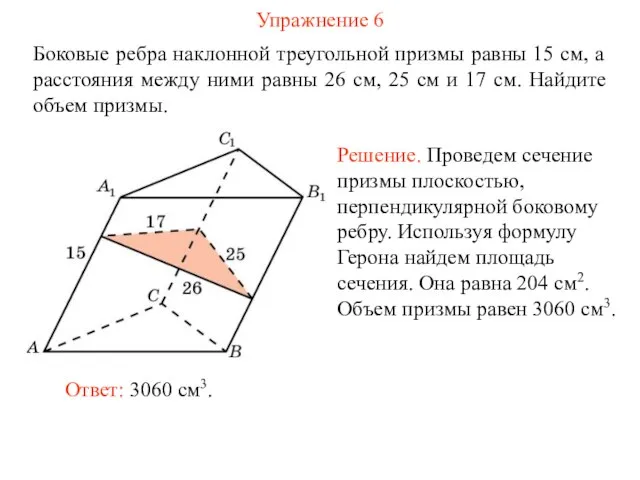
Упражнение 6

Боковые ребра наклонной треугольной призмы равны 15 см, а расстояния

Упражнение 7

Основанием призмы является параллелограмм со сторонами 1, 2 и острым

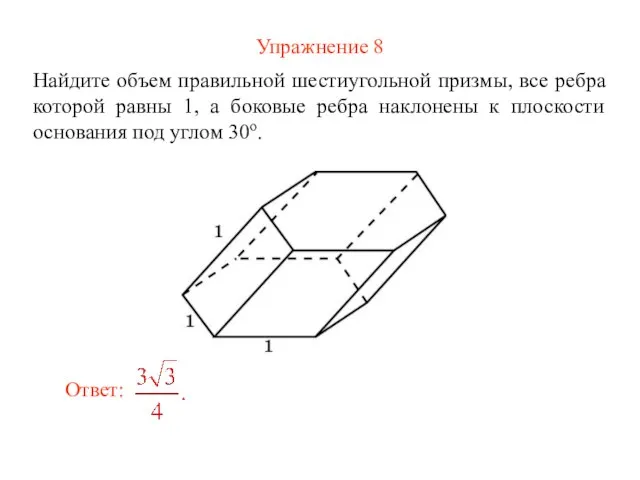
Упражнение 8

Найдите объем правильной шестиугольной призмы, все ребра которой равны 1,

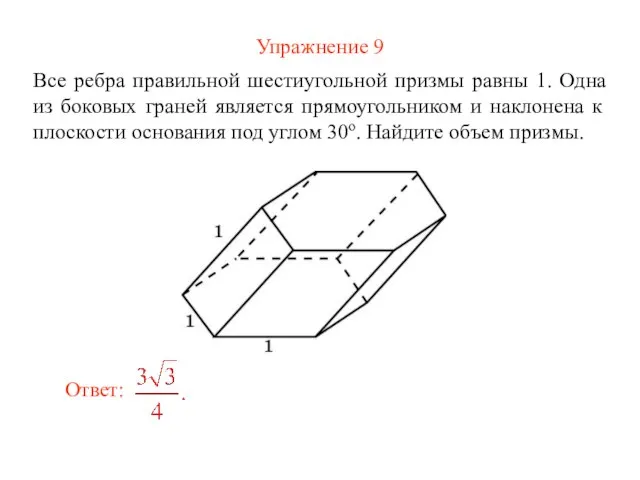
Упражнение 9

Все ребра правильной шестиугольной призмы равны 1. Одна из боковых

Упражнение 10

В основаниях призмы квадраты. Верно ли, что любая плоскость, проходящая

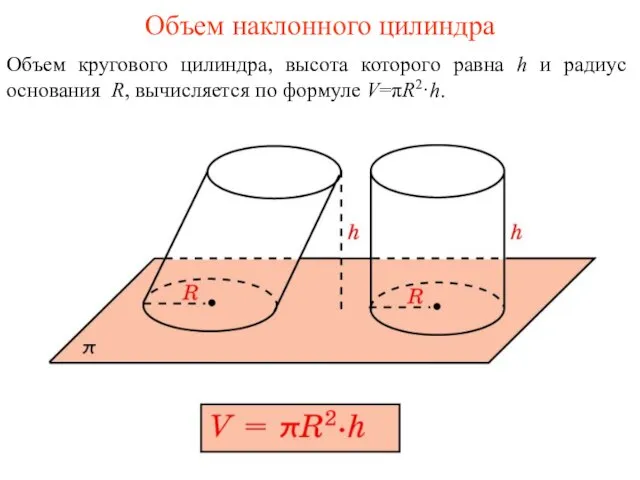
Объем наклонного цилиндра

Объем кругового цилиндра, высота которого равна h и радиус

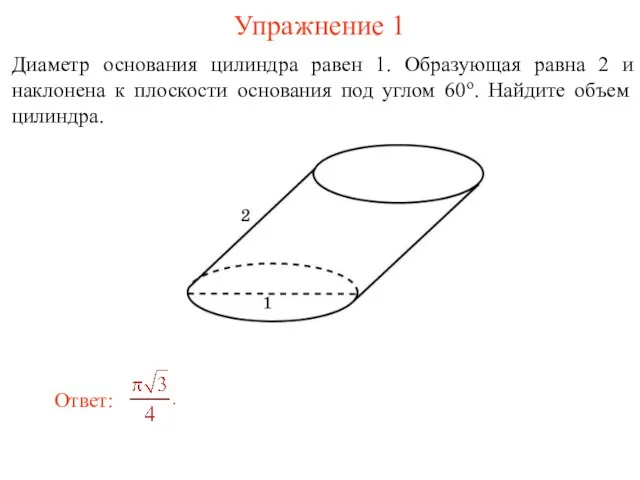
Упражнение 1

Диаметр основания цилиндра равен 1. Образующая равна 2 и наклонена

Упражнение 2

Верно ли, что любая плоскость, проходящая через центры оснований кругового

Упражнение 3

Два цилиндра имеют равные высоты, а площадь основания одного в

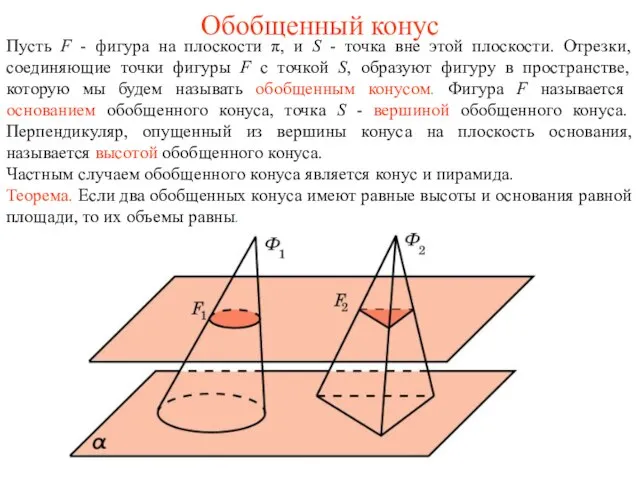
Обобщенный конус

Пусть F - фигура на плоскости π, и S -

Упражнение 1

Верно ли, что две пирамиды, имеющие общее основание и вершины,

Упражнение 2

Два конуса имеют равные высоты, а площадь основания одного в

Упражнение 3

Верно ли, что любая плоскость, проходящая через вершину и центр