§5. Некоторые теоретико-числовые приложения комбинаторики §5. Некоторые теоретико-числовые приложения комбинаторики Определение 1. Натуральное число называется простым, если оно имеет ровно два разных делите
Содержание
- 2. Примеры. Числа 2, 3, 5, 7, 11 простые, числа 4, 6, 18, 100 составные. Отметим, что
- 3. Теорема 2. Простых чисел существует бесконечно много. Доказательство. Допустим, существует лишь конечное число простых чисел. Перечислим
- 4. так как при делении на любое из этих чисел Р дает в остатке 1. Значит, допущение
- 5. Теорема3. (основная теорема арифметики). Для любого натурального числа а ≠ 1 имеет место равенство а =
- 6. Пример. 10 = 2 ∙ 5 = 21 ∙ 30 ∙ 51 , 81 = 34
- 7. Определение 4. Пусть а,b N. Число с называется общим делителем а и b , если оба
- 8. Теорема 5. Пусть и Число b является делителем а в том и только в том случае,
- 9. Следствие 6. Пусть для натурального числа а имеет место равенство Тогда число делителей а вычисляется по
- 10. Теорема 7. Пусть и Тогда число является общим делителем чисел а и b в том и
- 11. Определение 8. Число c называется наибольшим общим делителем чисел а и b (обозначение: с = НОД
- 12. Теорема 9. Пусть а и b натуральные числа, Тогда НОД (а,b)= где γi = min (αi,βi),
- 13. Следствие 10. Любой общий делитель чисел а и b является также делителем НОД (а, b). Определение
- 14. Пример. Пусть b =3. Тогда кратным ему будут числа 3,6, 9, 12, … . Их можно
- 15. Определение 12. Если число а делится на число b и с, то а называется общим кратным
- 16. Теорема 13. Пусть, Тогда число является общим кратным чисел b и с тогда и только тогда,
- 17. Доказательство. Пусть а – общее кратное b и с. Так как а делится на b, то
- 18. Определение 14. Самое маленькое из всех общих кратных натуральных чисел b и с называется наименьшим общим
- 19. Теорема 15. Пусть Число является НОК (b, с) в том и только в том случае, когда
- 20. Следствие 16. Любое общее кратное чисел b и с делится на НОК(b, с). Лемма 17. Для
- 21. Доказательство. Рассмотрим три случая: 1) х = у, тогда max (x, y) = x, min (x,
- 22. Теорема 18. Для любых натуральных чисел b и с НОД (b, с) · НОК (b, с)
- 23. НОД(b,c)*НОК(b,c) = = =
- 24. Определение 19. Числа а и b называются взаимно простыми, если НОД (а, b) = 1. Другими
- 25. Определение 20. Функцией Эйлера φ (n) называется количество чисел меньших, либо равных n, которые взаимно просты
- 26. Теорема 21. Пусть n = , причем αi > 0 и ki kj (i j), i
- 28. Скачать презентацию




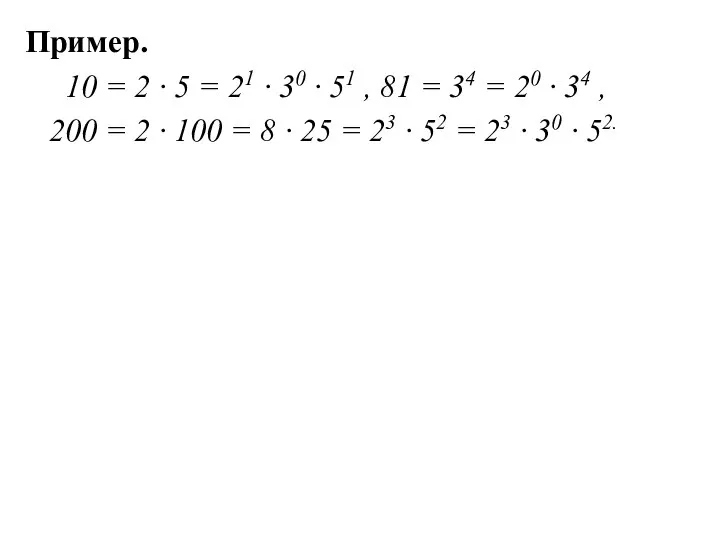
















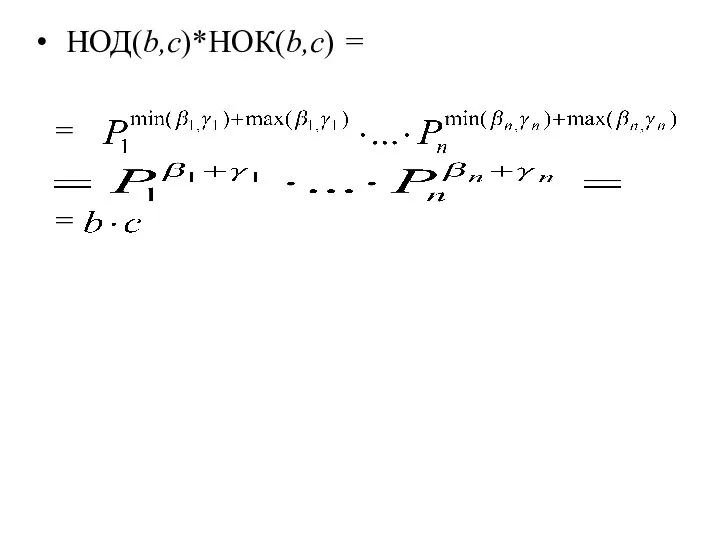



 Параллельные прямые
Параллельные прямые VIII Международная олимпиада по математике для I курсов ССУЗ
VIII Международная олимпиада по математике для I курсов ССУЗ Пропорция. 6 класс
Пропорция. 6 класс Линейные уравнения. Конкурс
Линейные уравнения. Конкурс Умножение разности двух выражений на их сумму
Умножение разности двух выражений на их сумму Вводное повторение.Геометрия 8 класс
Вводное повторение.Геометрия 8 класс Задача на кратчайший путь
Задача на кратчайший путь Своя игра по математике
Своя игра по математике График функции. Что мы знаем о графиках?
График функции. Что мы знаем о графиках? Сокращенные таблицы истинности
Сокращенные таблицы истинности Признаки делимости на 4, на 25
Признаки делимости на 4, на 25 Математика ЕГЭ. Вероятность. Часть I
Математика ЕГЭ. Вероятность. Часть I Устный счёт
Устный счёт Логарифмическая функция
Логарифмическая функция Урок математики в 6 «Б» классе 23.09.2013
Урок математики в 6 «Б» классе 23.09.2013 Наука геометрия для младших школьников. Диаметр
Наука геометрия для младших школьников. Диаметр Расстояние от точки до прямой. Перпендикулярные прямые
Расстояние от точки до прямой. Перпендикулярные прямые Дәрәҗәнең үзлекләре
Дәрәҗәнең үзлекләре Количественный счет предметов
Количественный счет предметов Четырехугольники: прямоугольник, ромб, квадрат, трапеция, параллелограмм
Четырехугольники: прямоугольник, ромб, квадрат, трапеция, параллелограмм Многоликая парабола
Многоликая парабола Графики основных элементарных функций
Графики основных элементарных функций Опять 25
Опять 25 Тригонометрические уравнения
Тригонометрические уравнения График линейной функции
График линейной функции Графики функций. Проверка домашнего задания
Графики функций. Проверка домашнего задания Геометрическая интерпретация комплексных чисел
Геометрическая интерпретация комплексных чисел Решение систем уравнений графически
Решение систем уравнений графически