Содержание
- 2. Ģeometriskie pārveidojumi
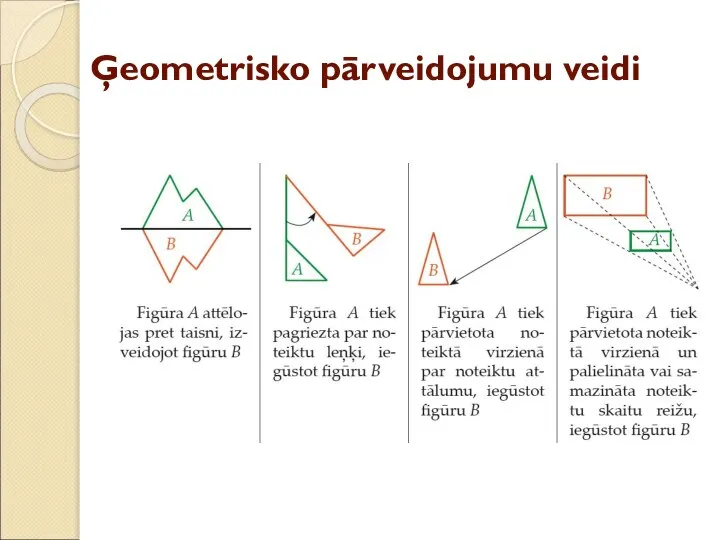
- 3. Ģeometrisko pārveidojumu veidi
- 4. Kas ir ģeometriskie pārveidojumi?
- 5. Paralēlā pārnese
- 6. Paralēlās pārneses jēdziens
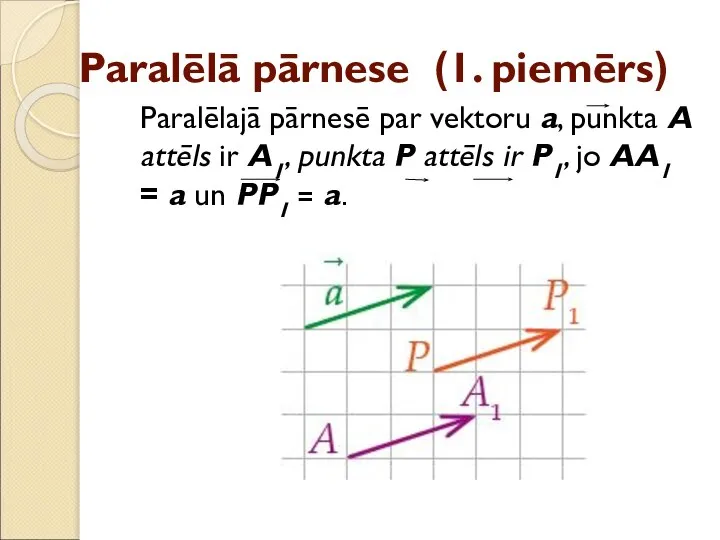
- 7. Paralēlā pārnese (1. piemērs) Paralēlajā pārnesē par vektoru a, punkta A attēls ir A1, punkta P
- 8. Paralēlā pārnese (2. piemērs)
- 9. Paralēlā pārnese (3. piemērs)
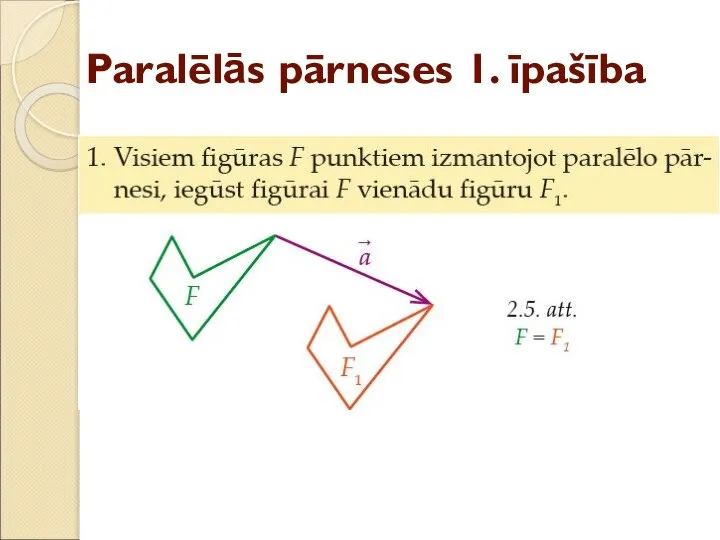
- 10. Paralēlās pārneses 1. īpašība
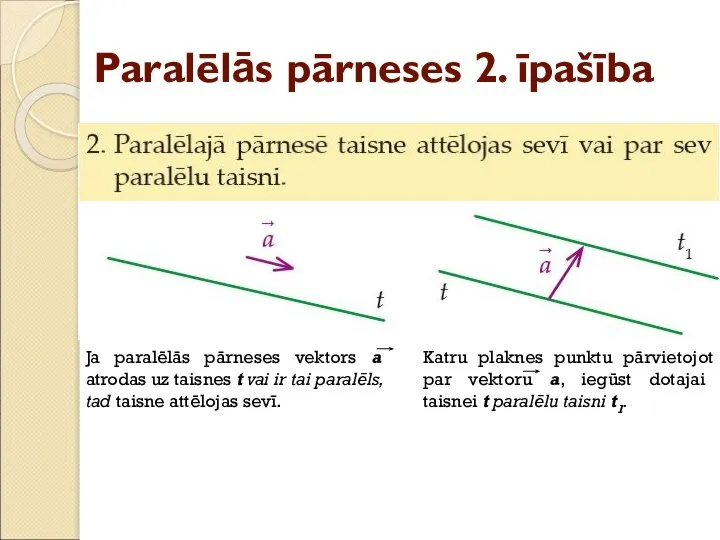
- 11. Paralēlās pārneses 2. īpašība Ja paralēlās pārneses vektors a atrodas uz taisnes t vai ir tai
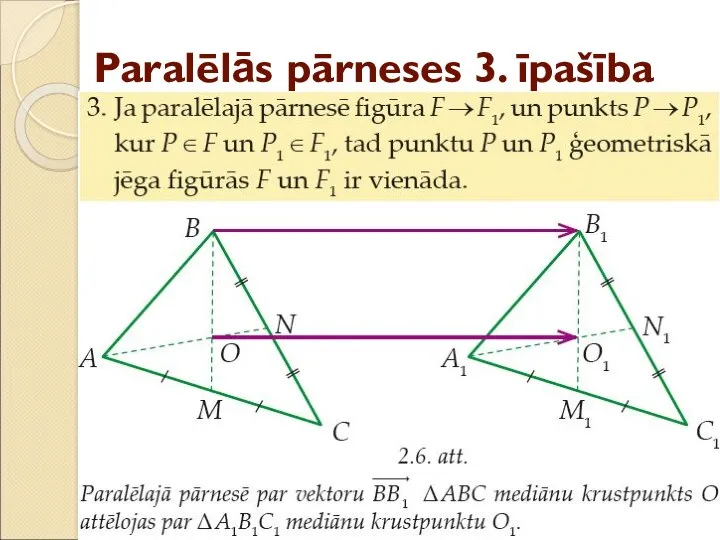
- 12. Paralēlās pārneses 3. īpašība
- 13. Paralēlās pārneses 4. īpašība Tā kā paralēlā pārnese ir plaknē definēta funkcija, kas pašu plakni attēlo
- 14. Aksiālā simetrija
- 15. Aksiālās simetrijas jēdziens
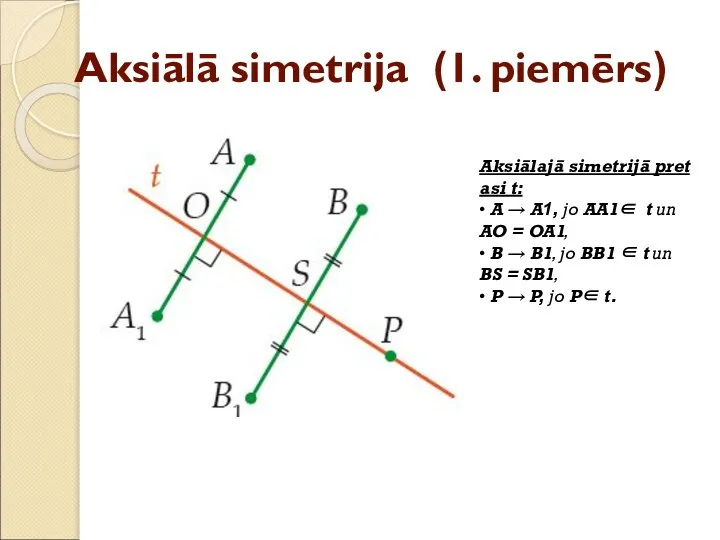
- 16. Aksiālā simetrija (1. piemērs) Aksiālajā simetrijā pret asi t: • A → A1, jo AA1∈ t
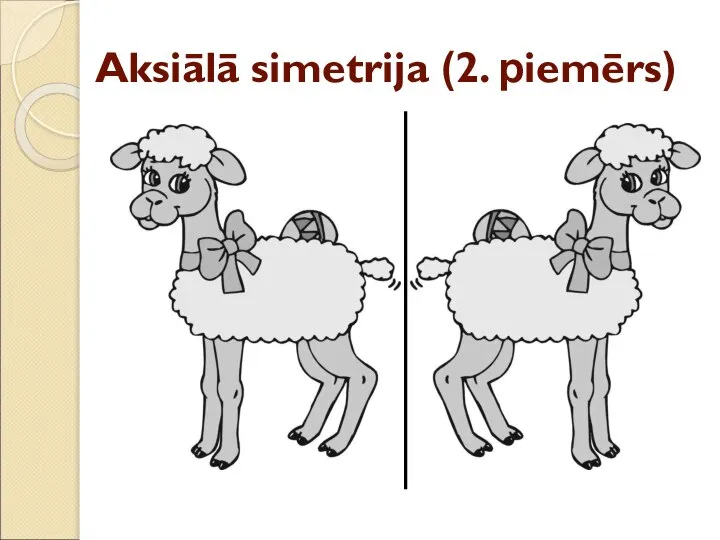
- 17. Aksiālā simetrija (2. piemērs)
- 18. Aksiālā simetrija (3. piemērs)
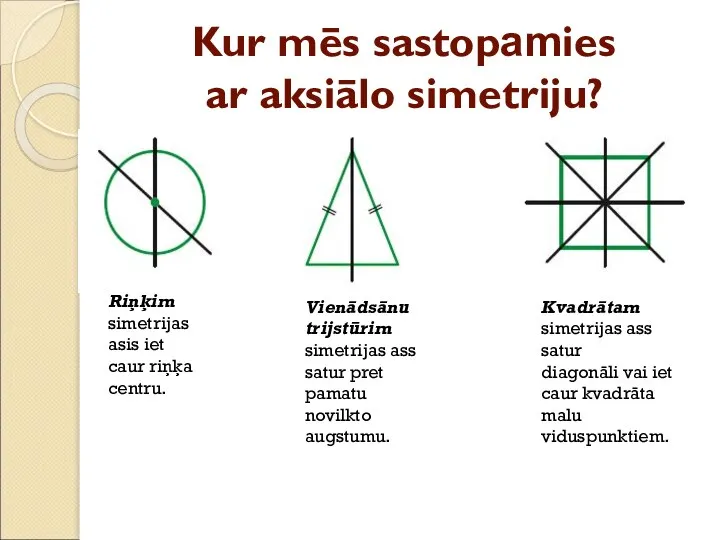
- 19. Kur mēs sastopamies ar aksiālo simetriju? Riņķim simetrijas asis iet caur riņķa centru. Vienādsānu trijstūrim simetrijas
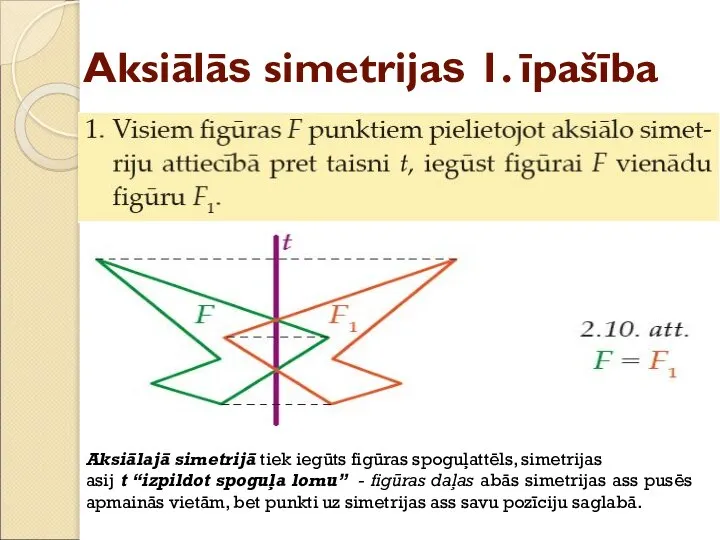
- 20. Aksiālās simetrijas 1. īpašība Aksiālajā simetrijā tiek iegūts figūras spoguļattēls, simetrijas asij t “izpildot spoguļa lomu”
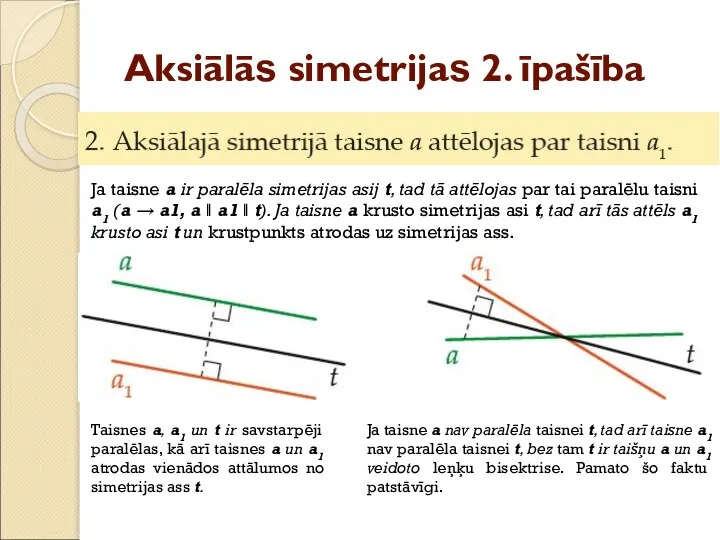
- 21. Aksiālās simetrijas 2. īpašība Ja taisne a ir paralēla simetrijas asij t, tad tā attēlojas par
- 22. Aksiālās simetrijas 3. īpašība Tā kā simetrijā pret asi pusplaknes attēlojas viena par otru, tad acīmredzami,
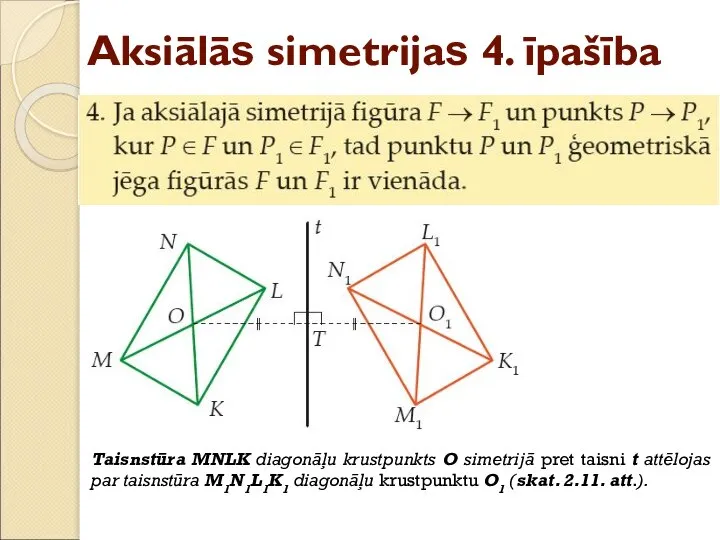
- 23. Aksiālās simetrijas 4. īpašība Taisnstūra MNLK diagonāļu krustpunkts O simetrijā pret taisni t attēlojas par taisnstūra
- 24. Pagrieziens
- 25. Pagrieziena jēdziens
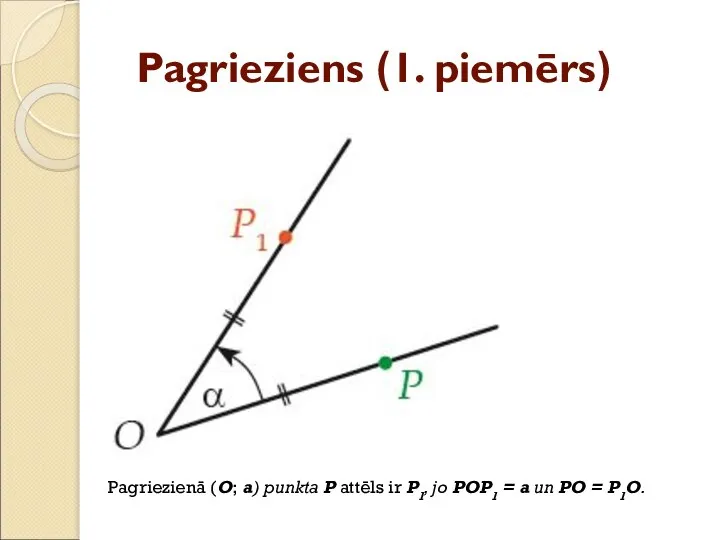
- 26. Pagrieziens (1. piemērs) Pagriezienā (O; a) punkta P attēls ir P1, jo POP1 = a un
- 27. Pagrieziens (2. piemērs)
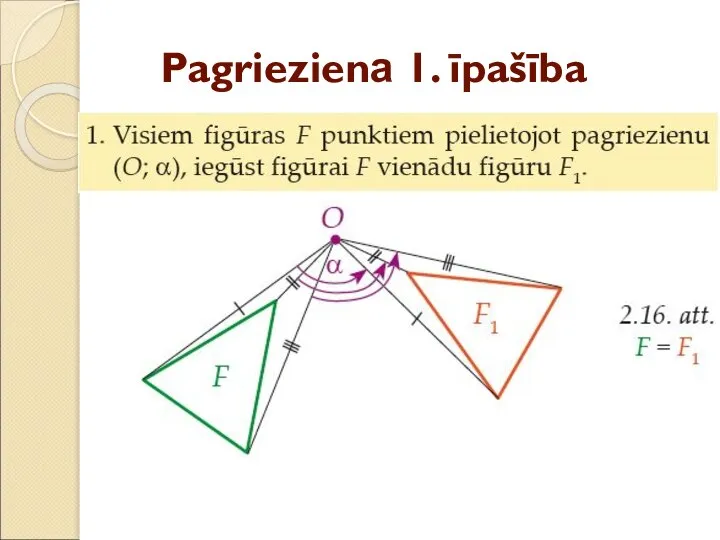
- 28. Pagrieziena 1. īpašība
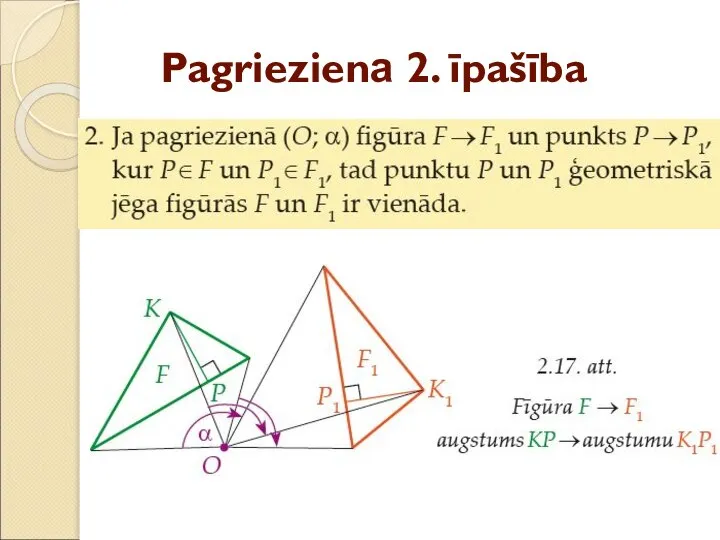
- 29. Pagrieziena 2. īpašība
- 30. Pagrieziena 3. īpašība Apskatīsim taisnstūra ABCD pagriezienu par 90° leņķi (B; + 90°) (skat. 2.18. att.).
- 31. Pagrieziena 4. īpašība
- 32. Pagrieziens par ± 180° un ± 360°
- 33. Homotētija
- 34. Homotētijas jēdziens
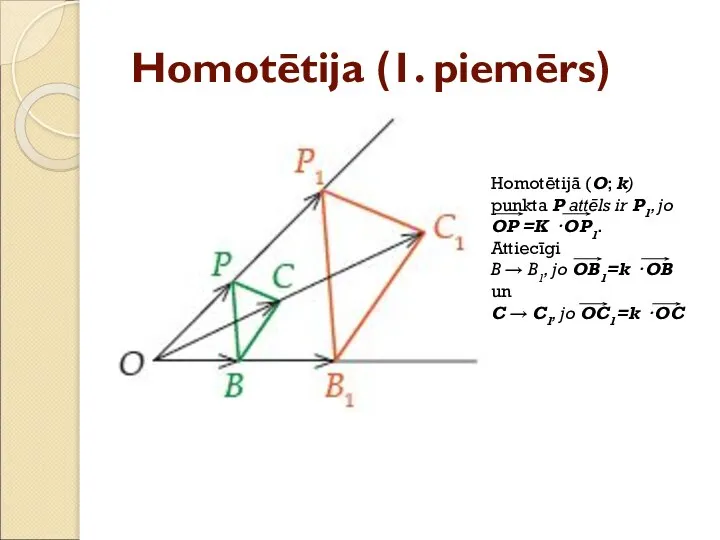
- 35. Homotētija (1. piemērs) Homotētijā (O; k) punkta P attēls ir P1, jo OP =K · OP1.
- 36. Homotētija (2. piemērs)
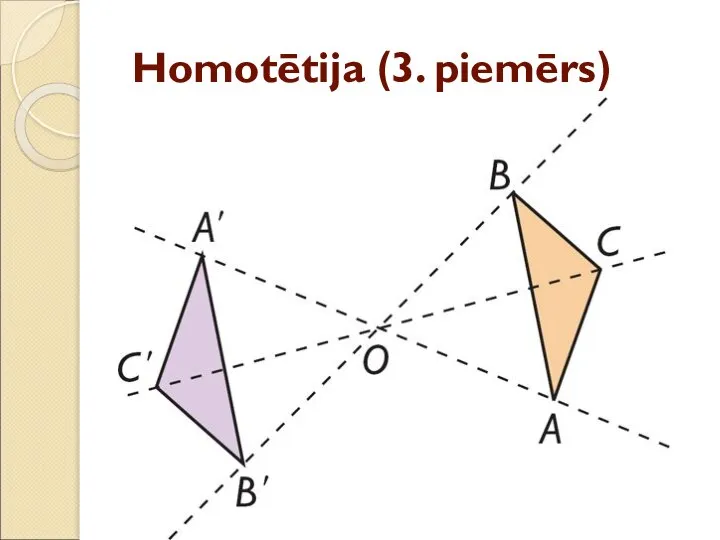
- 37. Homotētija (3. piemērs)
- 38. No ka ir atkarīga homotētija? Homotētijā, atkarībā no koeficienta k vērtības, veicot attēla konstrukciju, svarīgi ņemt
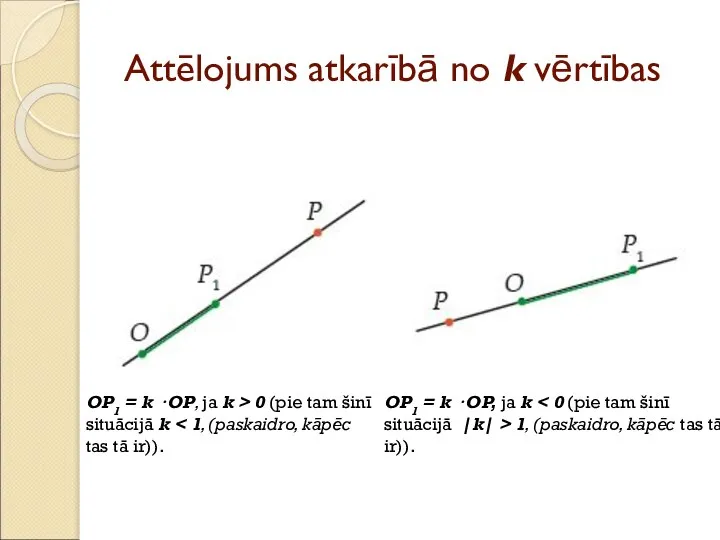
- 39. Attēlojums atkarībā no k vērtības OP1 = k · OP, ja k > 0 (pie tam
- 40. Homotētijas 1. īpašība
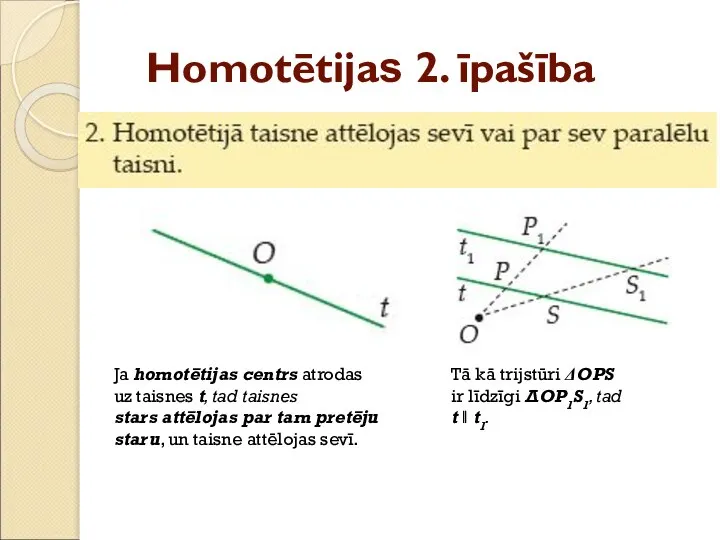
- 41. Homotētijas 2. īpašība Ja homotētijas centrs atrodas uz taisnes t, tad taisnes stars attēlojas par tam
- 42. Homotētijas 3. īpašība Acīmredzot, ja homotētijā (O; k), kur k > 0, punkts P → P1,
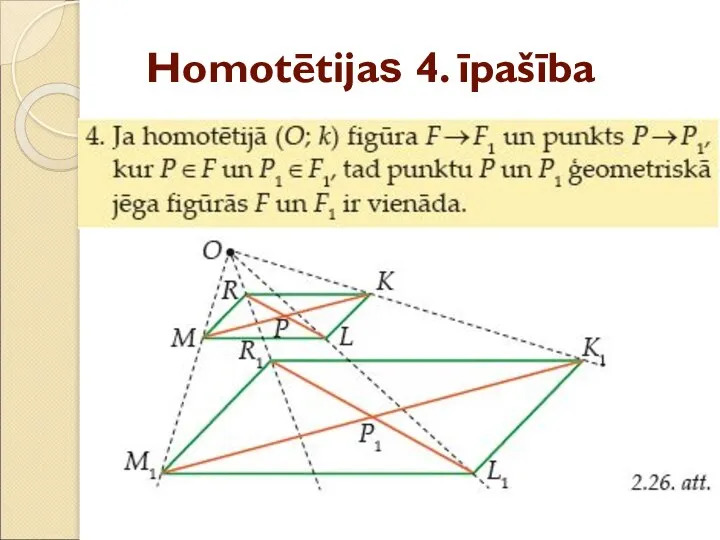
- 43. Homotētijas 4. īpašība
- 45. Скачать презентацию





















 Неравенства второй степени с одной переменной
Неравенства второй степени с одной переменной Теорема Виета. Теорема, обратная теореме Виета
Теорема Виета. Теорема, обратная теореме Виета Математические игры со спичками
Математические игры со спичками Множественная регрессия и корреляция
Множественная регрессия и корреляция тест по геометрии
тест по геометрии Функция, область определения, значения, четность. Автор: Горбунова В. И., учитель математик
Функция, область определения, значения, четность. Автор: Горбунова В. И., учитель математик Системы случайных величин
Системы случайных величин Матрицы и действия над ними
Матрицы и действия над ними Приложение к уроку математики (2 класс)
Приложение к уроку математики (2 класс) Презентация по математике "Задачи линейного программирования" - скачать
Презентация по математике "Задачи линейного программирования" - скачать  Деление трехзначного числа на двухзначное
Деление трехзначного числа на двухзначное Показательное распределение
Показательное распределение Числовые функции. 10 класс
Числовые функции. 10 класс Таблиця множення на 3
Таблиця множення на 3 Презентация по математике "Виды треугольников 7 класс" - скачать
Презентация по математике "Виды треугольников 7 класс" - скачать  ОГЭ 2018. Модуль «Геометрия»
ОГЭ 2018. Модуль «Геометрия» Сложение и вычитание десятичных дробей. Учитель математики Вечканова О.И.
Сложение и вычитание десятичных дробей. Учитель математики Вечканова О.И.  Решение тригонометрических уравнений
Решение тригонометрических уравнений Деление с остатком (3 класс)
Деление с остатком (3 класс) Функция. Область определения функции. Область значений функции. Алгебра 9 класс
Функция. Область определения функции. Область значений функции. Алгебра 9 класс Построение графиков квадратичной функции
Построение графиков квадратичной функции Аттестационная работа. Программа курса внеурочной деятельности по общеинтеллектуальному направлению «ЛЕГО»
Аттестационная работа. Программа курса внеурочной деятельности по общеинтеллектуальному направлению «ЛЕГО» Геометрия в нашем доме
Геометрия в нашем доме «Концентр 1000, нумерация и сравнение чисел» В.Н.Рудницкая (Начальная школа XXI века)
«Концентр 1000, нумерация и сравнение чисел» В.Н.Рудницкая (Начальная школа XXI века) Возрастание и убывание функции
Возрастание и убывание функции Теорема Пифагора
Теорема Пифагора Движение в пространстве. (10 класс)
Движение в пространстве. (10 класс) Математические и статистические методы обработки научных данных
Математические и статистические методы обработки научных данных