Содержание
- 2. Изучает свойства геометрических фигур на плоскости Изучает свойства фигур в пространстве В переводе с греческого слово
- 3. Планиметрия Стереометрия Наряду с этими фигурами мы будем рассматривать геометрические тела и их поверхности. Например, многогранники.
- 4. ГЕОМЕТРИЯ возникла из практических задач людей; ГЕОМЕТРИЯ лежит в основе всей техники и большинства изобретений человечества;
- 5. Интуитивное, живое пространственное воображение в сочетании со строгой логикой мышления — это ключ к изучению стереометрии
- 6. Для обозначение точек используем прописные латинские буквы Для обозначение прямых используем строчные латинские буквы Или обозначаем
- 7. Плоскости будем обозначать греческими буквами. На рисунках плоскости обозначаются в виде параллелограммов. Плоскость как геометрическую фигуру
- 8. C 25.10.2020 www.konspekturoka.ru
- 9. Аксиомы стереометрии Слово «аксиома» греческого происхождения и в переводе означает истинное, исходное положение теории. Система аксиом
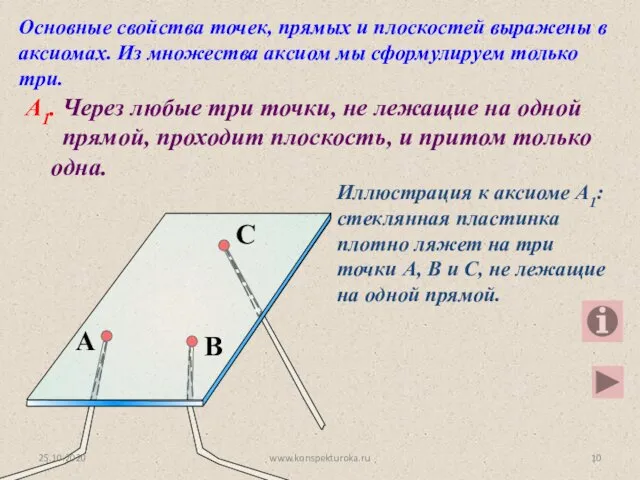
- 10. Основные свойства точек, прямых и плоскостей выражены в аксиомах. Из множества аксиом мы сформулируем только три.
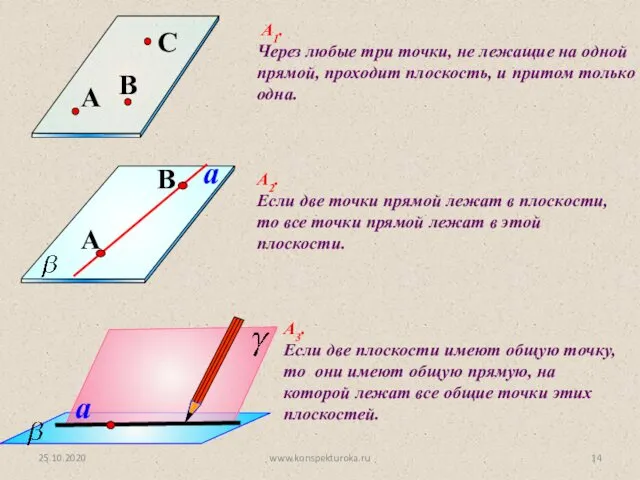
- 11. a А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой
- 12. Из аксиомы А2 следует, что если прямая не лежит в данной плоскости, то она имеет с
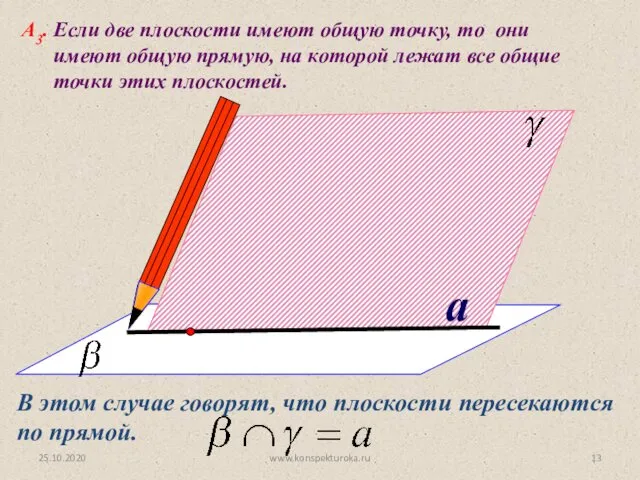
- 13. a А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат
- 14. А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
- 15. СЛЕДСТВИЯ ИЗ АКСИОМ Т-1 Через любую прямую и не принадлежащую ей точку можно провести плоскость, и
- 16. СЛЕДСТВИЯ ИЗ АКСИОМ Т-2 Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну.
- 18. Скачать презентацию












 Определение вероятности
Определение вероятности Уравнения
Уравнения Лекция 1. Основные понятия теории вероятности
Лекция 1. Основные понятия теории вероятности Объем
Объем Собирательные числительные
Собирательные числительные Простые дроби
Простые дроби Загадочное число Пи
Загадочное число Пи Количественный и порядковй счет
Количественный и порядковй счет Основные законы распределения, применяемые при обработке данных научного эксперимента. (Лекция 2)
Основные законы распределения, применяемые при обработке данных научного эксперимента. (Лекция 2) Свойства функции
Свойства функции Математический марафон
Математический марафон Задачи на нахождение остатка . Часть 2
Задачи на нахождение остатка . Часть 2 Презентация по математике "ЧИСЛО 10. СОСТАВ ЧИСЛА 10" - скачать бесплатно
Презентация по математике "ЧИСЛО 10. СОСТАВ ЧИСЛА 10" - скачать бесплатно УРОК МАТЕМАТИКИ В 5 КЛАССЕ ТЕМА: СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ Учитель математики МОУ Таганаевской СОШ
УРОК МАТЕМАТИКИ В 5 КЛАССЕ ТЕМА: СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ Учитель математики МОУ Таганаевской СОШ Классическая теория вероятности. 6 и 11 класс
Классическая теория вероятности. 6 и 11 класс Решение уравнений. 5 класс
Решение уравнений. 5 класс Круг. Окружность. Длина окружности. Площадь круга. 6 класс
Круг. Окружность. Длина окружности. Площадь круга. 6 класс Тригонометрический круг, определение синуса, косинуса, тангенса и котангенса
Тригонометрический круг, определение синуса, косинуса, тангенса и котангенса Геометрический турнир
Геометрический турнир Презентация по математике "Функция арифметического квадратного корня, её свойства" - скачать бесплатно
Презентация по математике "Функция арифметического квадратного корня, её свойства" - скачать бесплатно Что такое уравнение
Что такое уравнение Приближенные решения алгебраических и трансцендентных уравнений
Приближенные решения алгебраических и трансцендентных уравнений Функции и их свойства
Функции и их свойства Решение задач на проценты. Уравнения
Решение задач на проценты. Уравнения Равнобедренный треугольник. Решение задач
Равнобедренный треугольник. Решение задач Комбинаторика элементтері
Комбинаторика элементтері Способы решения показательных уравнений
Способы решения показательных уравнений Умножение десятичных дробей на натуральные числа. 5 класс Ермолаева Ирина Николаевна, учитель математики МБОУ «Новошешминск
Умножение десятичных дробей на натуральные числа. 5 класс Ермолаева Ирина Николаевна, учитель математики МБОУ «Новошешминск