Содержание
- 2. Лекция 2 Алгебра матриц I. Операции над матрицами. 2. Обратная матрица. 3. Решение матричных уравнений. 4.
- 3. Операции над матрицами. Определим несколько операций над матрицами. I. Равенство матриц . II. Сложение матриц .
- 4. III. Умножение матрицы на число. IV. Умножение матриц. Здесь:
- 6. Правило умножения матриц : 1. Перемножать можно лишь матрицы определённых размеров (число столбцов матрицы левой равно
- 7. Пример.
- 9. Свойства операции сложения: Рассмотрим матрицы размера (m x n) : 1. 2. Свойства операций умножения на
- 10. 2. 3. 4. 5. 6. (AB)T = BT AT 7. det(AB) = det(A) det(B)
- 11. Обратная матрица. ( квадратные матрицы, Е – единичная матрица). матрица А называется невырожденной.
- 12. Теорема существования и единственности обратной матрицы. Для всякой невырожденной матрицы существует единственная обратная матрица, вычисляемая по
- 13. Убедимся, что по указанной формуле находится именно обратная матрица. Вычислим произведение
- 14. Точно также можно показать, что Таким образом, действительно
- 15. б)Единственность (показать самостоятельно). Пример. Решение. 1. 2. 3. 4.
- 16. Решение матричных уравнений. Пусть А– известная квадратная матрица порядка n , В– известная матрица размера (n
- 17. Точно также решаются и другие типы уравнений : Невырожденные системы n линейных уравнений с n неизвестными
- 18. Обозначим - матрица столбец из неизвестных, – матрица из коэффициентов перед неизвестными, – матрица столбец из
- 19. Систему (*) тогда можно записать в виде:
- 20. Если А– невырожденная матрица, то существует единственное решение этого матричного уравнения или, в поэлементной записи (1)
- 21. Здесь - определитель системы, -определитель, полученный из определителя системы заменой i-столбца на столбец свободных членов. Формулы
- 22. Вывод: Если определитель системы n линейных уравнений с n неизвестными отличен от нуля, то существует единственное
- 23. Ранг матрицы и его вычисление методом элементарных преобразований. Выделим в матрице размера (m x n) произвольные
- 27. Найдите ранг матрицы:
- 28. Найдите ранг матрицы
- 29. МИКРОТЕСТ 2 1. Квадратную матрицу A 4-го порядка (n-го) умножили на число k≠0. Во сколько раз
- 31. Скачать презентацию

























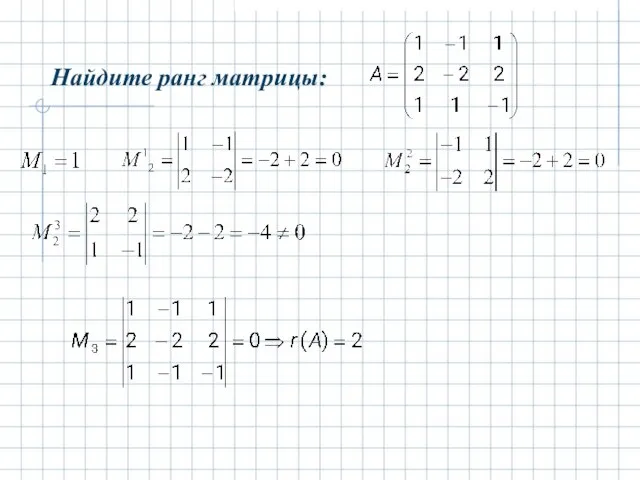


 Решение нелинейных уравнений
Решение нелинейных уравнений Внеклассное мероприятие Что? Где? Когда в 9 – 11 классах
Внеклассное мероприятие Что? Где? Когда в 9 – 11 классах Тайна чисел. Числовые суеверия.
Тайна чисел. Числовые суеверия. Симплекс-метод
Симплекс-метод Градусная мера дуги
Градусная мера дуги История развития математики в Индии
История развития математики в Индии Математика в сказках
Математика в сказках Элементы дифференциального исчисления Лекция 4
Элементы дифференциального исчисления Лекция 4  Основные свойства неопределенного интервала
Основные свойства неопределенного интервала Параллельные прямые
Параллельные прямые Введение в асимптотические методы. Лекция 4. Интегралы: нелокальные вклады
Введение в асимптотические методы. Лекция 4. Интегралы: нелокальные вклады Теорема Ербрана. (Лекция 4)
Теорема Ербрана. (Лекция 4) Презентация на тему: Длина
Презентация на тему: Длина Модель плоскости
Модель плоскости Законы арифметических действий
Законы арифметических действий Построение правильных многоугольников
Построение правильных многоугольников Аттестационная работа. Лабораторная работа. Композиция преобразований плоских фигур
Аттестационная работа. Лабораторная работа. Композиция преобразований плоских фигур Формулы суммы и разности одноименных тригонометрических функций
Формулы суммы и разности одноименных тригонометрических функций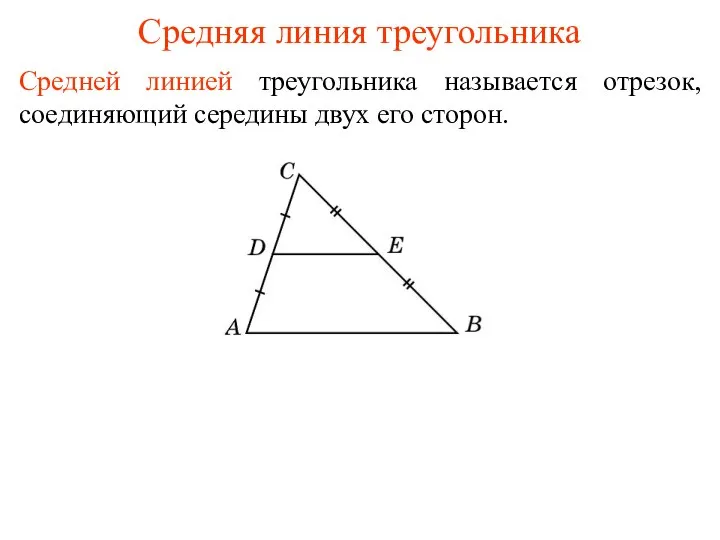 Средняя линия треугольника
Средняя линия треугольника Сумма углов треугольника
Сумма углов треугольника Одночлены. Арифметические операции над одночленами. 7 класс
Одночлены. Арифметические операции над одночленами. 7 класс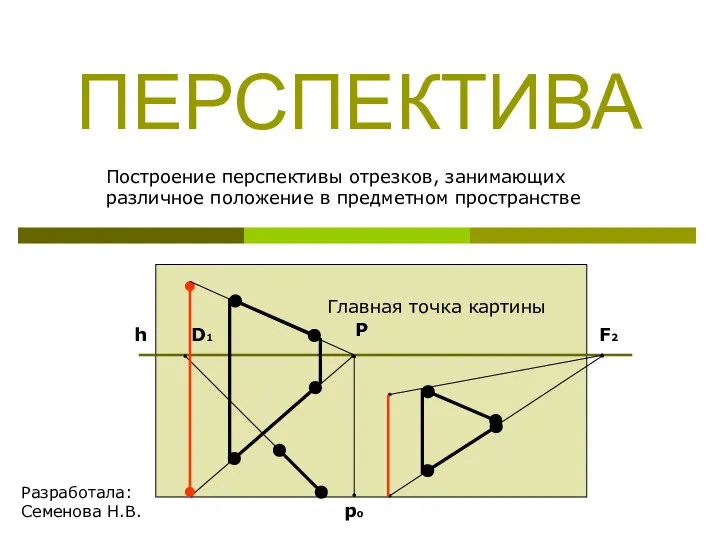 Построение перспективы отрезков, занимающих различное положение в предметном пространстве
Построение перспективы отрезков, занимающих различное положение в предметном пространстве Математика. Примеры
Математика. Примеры Рене Декарт (1596 -1650)
Рене Декарт (1596 -1650) Векторы в пространстве
Векторы в пространстве Күпбуын һәм аның стандарт рәвеше
Күпбуын һәм аның стандарт рәвеше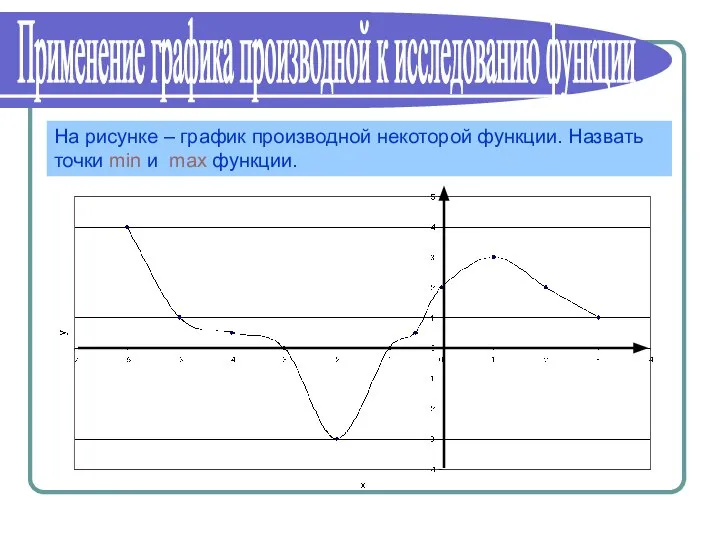 Применение графика производной к исследованию функции
Применение графика производной к исследованию функции Цифры и числа. 5 класс
Цифры и числа. 5 класс