Содержание
- 2. Основные методы решения геометрических задач: геометрический – требуемое утверждение выводится с помощью логических рассуждений из ряда
- 3. Задача 1. Медиана АМ треугольника АВС равна отрезку ВМ. Доказать, что один из углов треугольника АВС
- 4. Задача 4 (признак прямоугольного треугольника по медиане). Доказать, что если медиана треугольника равна половине стороны, к
- 5. Свойства площадей. Площади многоугольников Следствие из теоремы о площади треугольника. Если высоты двух треугольников равны, то
- 6. Теоремы о точках пересечения чевиан Теорема. В любом треугольнике медианы пересекаются в одной точке (центроид, центр
- 7. Задача 8. Найти отношение суммы квадратов медиан треугольника к сумме квадратов всех его сторон. Одним из
- 8. Свойство биссектрисы внутреннего угла треугольника. Биссектриса внутреннего угла треугольника делит противоположную сторону на части, пропорциональные заключающим
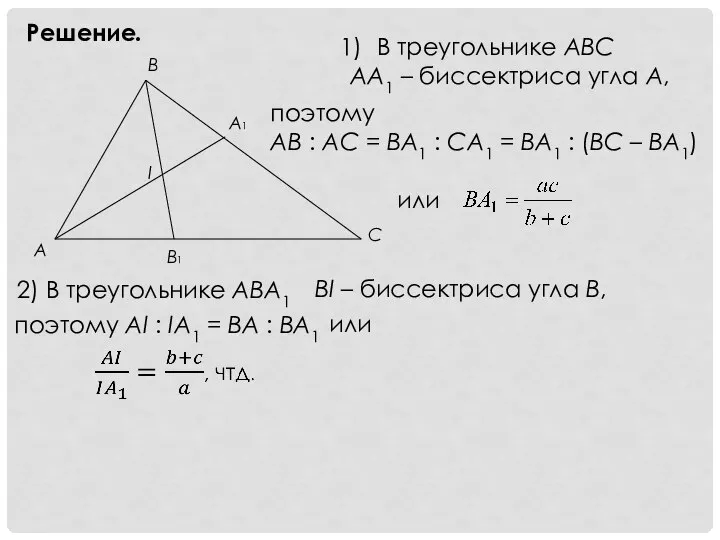
- 9. Решение. В треугольнике ABC AA1 – биссектриса угла A, поэтому AB : AC = BA1 :
- 10. Теорема. В любом треугольнике высоты пересекаются в одной точке (ортоцентр треугольника). Теорема о серединном перпендикуляре к
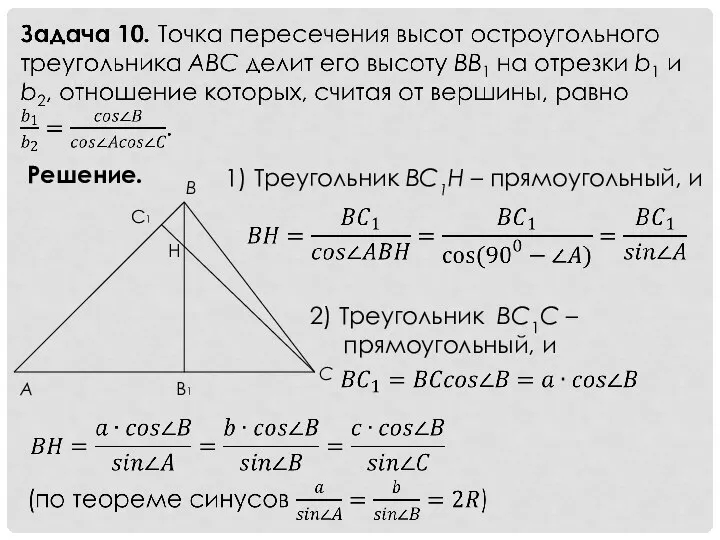
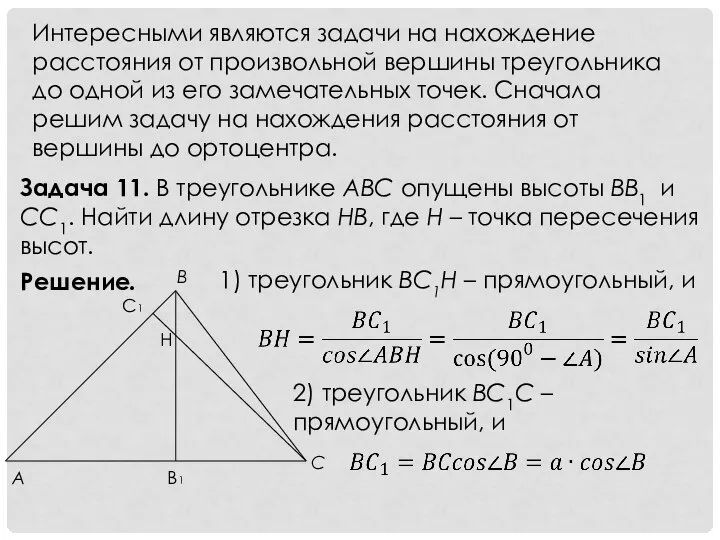
- 11. Решение. 1) Tреугольник BC1Н – прямоугольный, и 2) Треугольник BC1C – прямоугольный, и
- 12. Используя формулы приведения. Откуда Замечание. Если один из углов тупой, то в (*) соответствующий косинус нужно
- 13. Интересными являются задачи на нахождение расстояния от произвольной вершины треугольника до одной из его замечательных точек.
- 14. Задача 12. Найти расстояние от вершины B треугольника ABC до ортоцентра, если Решение. По теореме косинусов
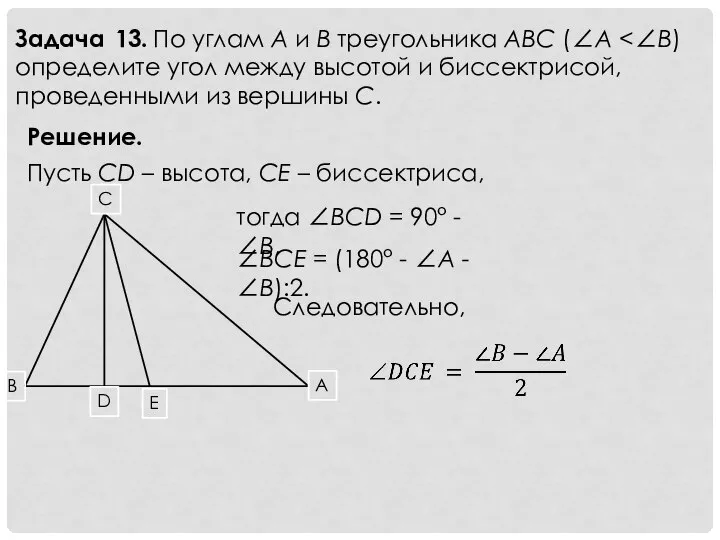
- 15. Задача 13. По углам A и B треугольника ABC (∠A Решение. Пусть CD – высота, CE
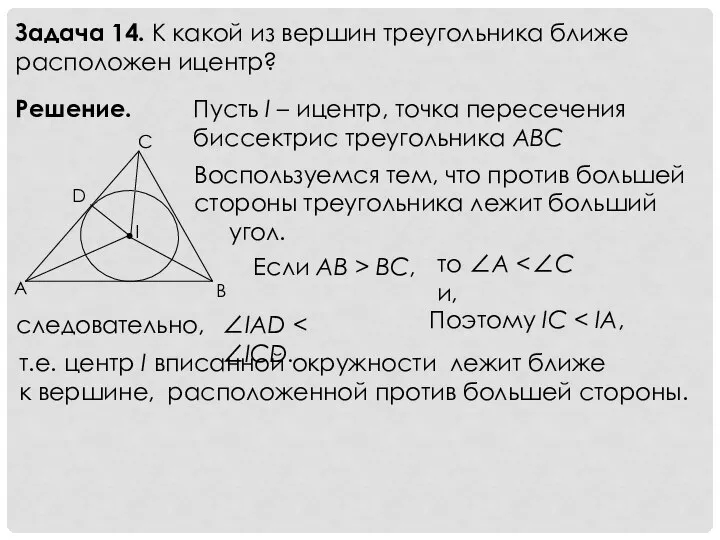
- 16. Задача 14. К какой из вершин треугольника ближе расположен ицентр? Решение. Пусть I – ицентр, точка
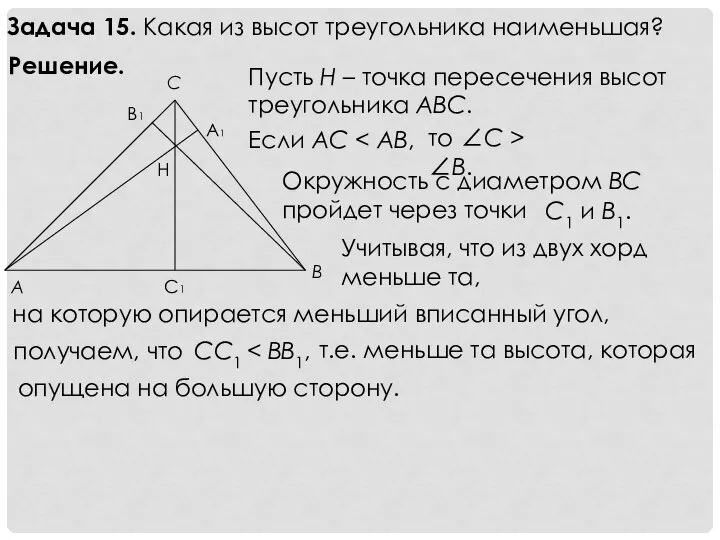
- 17. Задача 15. Какая из высот треугольника наименьшая? Решение. Пусть Н – точка пересечения высот треугольника ABC.
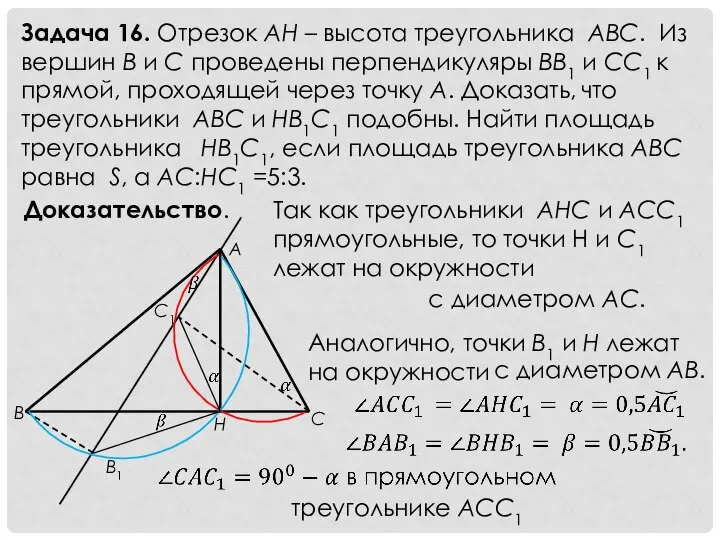
- 18. Задача 16. Отрезок АН – высота треугольника АВС. Из вершин В и С проведены перпендикуляры ВВ1
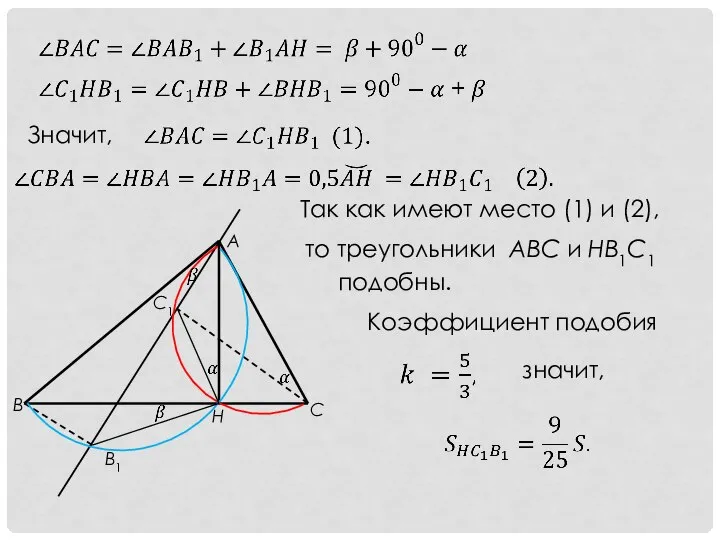
- 19. Значит, Так как имеют место (1) и (2), то треугольники АВС и НВ1С1 подобны. Коэффициент подобия
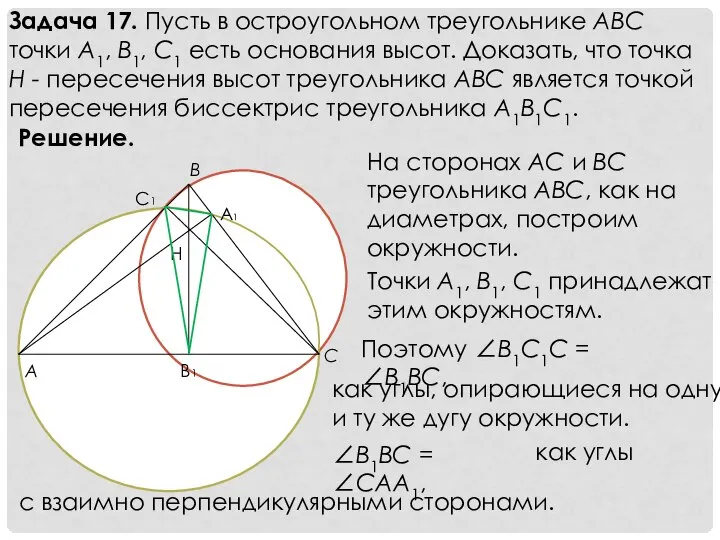
- 20. Задача 17. Пусть в остроугольном треугольнике ABC точки A1, B1, C1 есть основания высот. Доказать, что
- 22. Скачать презентацию










 Загальні відомості про засоби вимірювань
Загальні відомості про засоби вимірювань Множества (числовые и не только)
Множества (числовые и не только) Математическая статистика - наука о принятии решений в условиях неопределенности
Математическая статистика - наука о принятии решений в условиях неопределенности Высказывания с кванторами в начальном курсе математики
Высказывания с кванторами в начальном курсе математики Пирамида. Виды пирамид
Пирамида. Виды пирамид Сочетательное и распределительное свойства умножения
Сочетательное и распределительное свойства умножения Сложение дробей с разными знаменателями
Сложение дробей с разными знаменателями Преобразование переменных в парной регрессии
Преобразование переменных в парной регрессии Смешанные дроби
Смешанные дроби Урок геометрии в 7 классе. Треугольники
Урок геометрии в 7 классе. Треугольники Функция и ее график
Функция и ее график Натуральні числа
Натуральні числа Презентация на тему Решение уравнений с модулем
Презентация на тему Решение уравнений с модулем  Первый признак равенства треугольников
Первый признак равенства треугольников Предельные величины, эластичности
Предельные величины, эластичности Понятие логарифма, основные свойства логарифмов
Понятие логарифма, основные свойства логарифмов Презентация на тему Правильные выпуклые многогранники
Презентация на тему Правильные выпуклые многогранники Повтарение по математике. Уравнение
Повтарение по математике. Уравнение Изображение пространственных фигур
Изображение пространственных фигур Свойства параллелограмма
Свойства параллелограмма Математика 3 класс «Умножение и деление многозначного числа на однозначное» Программа «Школа 2000»
Математика 3 класс «Умножение и деление многозначного числа на однозначное» Программа «Школа 2000»  Приёмы решения практико-ориентированных задач ОГЭ (9 класс)
Приёмы решения практико-ориентированных задач ОГЭ (9 класс) Нахождение числа по его дроби
Нахождение числа по его дроби Численные методы безусловной оптимизации. Метод Хука-Дживса (метод прямого поиска)
Численные методы безусловной оптимизации. Метод Хука-Дживса (метод прямого поиска) Умножение. Координаты точки
Умножение. Координаты точки Объём. Объём прямоугольного параллелепипеда и куба
Объём. Объём прямоугольного параллелепипеда и куба Основные методы решения тригонометрических уравнений
Основные методы решения тригонометрических уравнений Счет
Счет