Содержание
- 2. Question 1. A sequence an, n = 1,2,3,…, satisfies a) Use the definition of limit to
- 3. b) Conclude that and find We have Therefore
- 4. Calculus++ Also known as Hysterical Calculus
- 5. Question 2. A sequence xn, n = 1,2,3,… is and the initial conditions x1 = a,
- 6. Thus, we found two sequences that satisfy the Do any of these sequences satisfy the initial
- 7. Let us check that this linear combination We have Well, we can consider linear combination of
- 8. Thus For the values of arbitrary constants c1 and c2 we obtain Now the limit is
- 9. The method of the week To find the sequence that satisfies the defining relationship and the
- 10. Question 3 a). Find the following limit Solution: We have
- 11. We have The obtained identity yields
- 12. Therefore we can use the following sandwich inequality Since sin x is a continuous function we
- 13. Question 4. State a (positive) definition of a divergent sequence {xn}. Solution: We begin with the
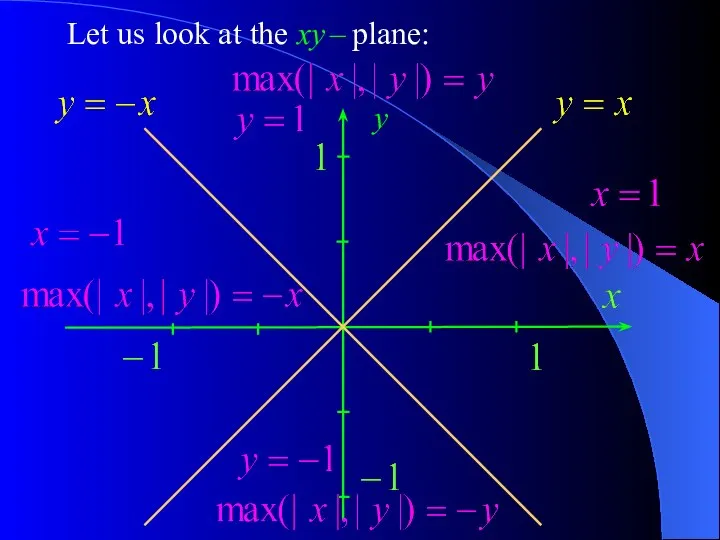
- 14. Question 5. Draw the curve defined by the in the x y – plane. Solution. To
- 15. Now we can find the limit Note the following double inequality Hence
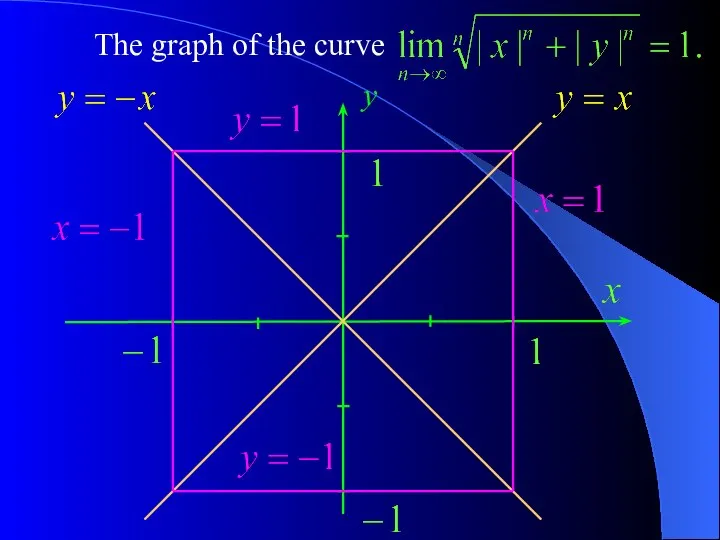
- 16. Since the sandwich theorem tells us that Thus, we have to draw the curve defined by
- 17. Let us look at the xy – plane: y
- 18. The graph of the curve y
- 19. Question 6. Use the definition of convergent sequence to obtain a sandwich inequality for the sequence
- 20. The definition tells us that for all Therefore we obtain the following sandwich inequality for our
- 22. Скачать презентацию

















 Презентация по математике "Квадрат" - скачать бесплатно
Презентация по математике "Квадрат" - скачать бесплатно Правила выполнения и оформления чертежей
Правила выполнения и оформления чертежей Тайны числа три
Тайны числа три Сложение и вычитание десятичных дробей. 18 февраля в истории Кубани
Сложение и вычитание десятичных дробей. 18 февраля в истории Кубани Приемы устного счета
Приемы устного счета Мера центральной тенденции
Мера центральной тенденции Раскрытие скобок
Раскрытие скобок Дробные выражения
Дробные выражения Презентация по математике "Сложение и вычитание десятичных дробей" - скачать бесплатно_
Презентация по математике "Сложение и вычитание десятичных дробей" - скачать бесплатно_ Уравнение линии
Уравнение линии Квадратный корень из дроби
Квадратный корень из дроби Упрощение выражений. 5 класс
Упрощение выражений. 5 класс Числовая прямая
Числовая прямая Разложение вектора по базису
Разложение вектора по базису Графическое решение систем уравнений Выполнила учитель математики ГОУ СОШ№208 Кухаренко Наталия Александровна
Графическое решение систем уравнений Выполнила учитель математики ГОУ СОШ№208 Кухаренко Наталия Александровна Линейная регрессия
Линейная регрессия Задания из открытого банка ЕГЭ
Задания из открытого банка ЕГЭ Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс Конкретный смысл действия деления. Выполни деление, используя рисунок
Конкретный смысл действия деления. Выполни деление, используя рисунок Отрезок. Треугольник. Многоугольники
Отрезок. Треугольник. Многоугольники Площадь. Формула площади прямоугольника
Площадь. Формула площади прямоугольника Рациональные числа 6 класс
Рациональные числа 6 класс  Алгебраический метод решения логических задач
Алгебраический метод решения логических задач Скалярное произведение векторов
Скалярное произведение векторов Своя игра. 6 класс
Своя игра. 6 класс ГБОУ СОШ № 1226
ГБОУ СОШ № 1226  Статистика. Необходимость возникновения статистики-науки
Статистика. Необходимость возникновения статистики-науки Ссора в царстве степенных функций
Ссора в царстве степенных функций