Содержание
- 2. Учебные вопросы: 1. Декартова система координат. Уравнение линии. Прямая на плоскости. 2. Кривые второго порядка.
- 3. Возьмем на плоскости две взаимно перпендикулярные координатные оси с общим началом О в точке пересечения. Одну
- 4. Прямая на плоскости Общее уравнение прямой на плоскости имеет вид , (1.1) где A, B, C
- 5. Уравнение прямой с угловым коэффициентом представляет собой уравнение, разрешенное относительно y: . (1.2) Здесь k –
- 6. Каноническое уравнение прямой имеет вид , а параметрическое – , (1.4) где - точка, лежащая на
- 7. Пример 1.1. Дана прямая . Выписать ее вектор нормали, найти угловой коэффициент, построить прямую на плоскости.
- 8. Пример 1.2. Привести к уравнению в отрезках прямую, заданную общим уравнением . Решение. Проведем преобразования общего
- 9. Угол ϕ между прямыми, заданными уравнениями с угловым коэффициентом ( , ), определяется с помощью формулы
- 10. Пример 1.3. Выбрать из прямых (I) – (V) параллельные и перпендикулярные, определить угол между прямыми (I)
- 11. Решение. Сначала для каждой прямой найдем угловой коэффициент: (I) (II) (III) (IV) (V) (VI)
- 12. Поскольку , , получаем, что прямые (I) и (III), (II) и (V) параллельны. С другой стороны,
- 13. Составление уравнений прямых. Рассмотрим основные типы возникающих задач. 1) Записать уравнение прямой с известным угловым коэффициентом
- 14. 3) Записать уравнение прямой, проходящей через заданную точку перпендикулярно прямой . Угловые коэффициенты перпендикулярных прямых связаны
- 15. Пример 1.4. Составить уравнение прямой, проходящей через точку A(2,-3) и образующей с положительным направлением оси OX
- 16. Пример1.5. Составить уравнения прямых, проходящих через точку A(2,-3) параллельно и перпендикулярно прямой . Решение. Так как
- 17. Пример 1.6. Написать уравнение прямой, проходящей через точки A(3;3), B(-1;5). Решение. Подставляя в (1.10) координаты данных
- 18. Пример 1.7. В треугольнике с вершинами O(0;0), A(3;3), B(-1;5) найти уравнения стороны AB, медианы AE и
- 19. Далее, высота OK – это прямая, проходящая через вершину O перпендикулярно прямой AB. Воспользуемся уравнением (11).
- 20. Кривые второго порядка Определение 2.1. Всякая линия, которая в некоторой системе координат описывается уравнением второй степени
- 21. Определение 2.2. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных
- 22. Тогда (рис. 1) фокусы имеют координаты . Пусть ‒текущая точка эллипса. Расстояние называются радиусами- векторами точки
- 23. Из определения эллипса следует, что , (2.3) а простой подсчет показывает, что (2.4) Разделив (2.4) на
- 24. Приравнивая в формулах (2.2) и (2.6), имеем: (2.7) Из условия 2а > 2с (сумма длин двух
- 25. 1) Если точка (х; у) лежит на эллипсе , то точка (х; -у) тоже лежит на
- 26. 3) Выражая из уравнения эллипса у явно через х, получаем . Область определения этой функции ,
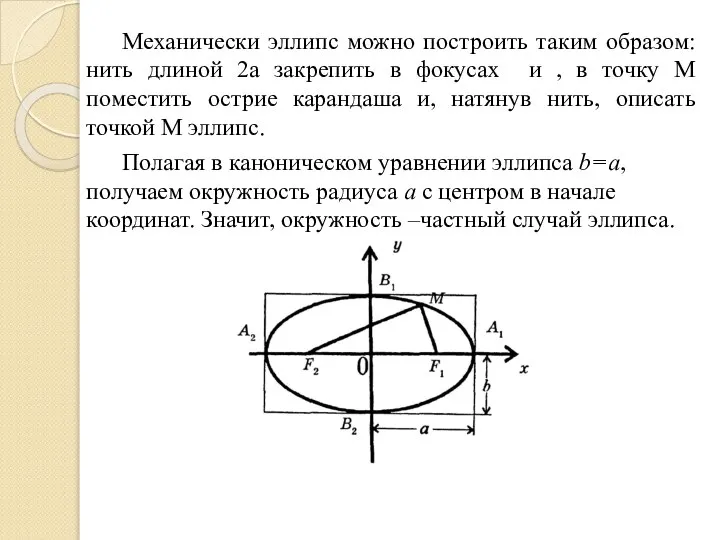
- 27. Механически эллипс можно построить таким образом: нить длиной 2а закрепить в фокусах и , в точку
- 28. Определение. Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большой оси . Из равенства или следуют
- 29. 2.2. ГИПЕРБОЛА. Определение. Гиперболой называется геометрическое место точек, для каждой из которых разность расстояний до двух
- 30. ВЫВОД УРАВНЕНИЯ Систему координат выбираем, как и в предыдущем случае (при выводе уравнения эллипса). Фокусы имеют
- 31. И тогда (2.10) Получили каноническое уравнение гиперболы.
- 32. ИССЛЕДОВАНИЕ ФОРМЫ ГИПЕРБОЛЫ 1) Если точка (х; у) лежит на гиперболе, то на гиперболе лежат точки
- 33. 3) Выразим у явно через х: . Эта функция определена когда и . Это говорит о
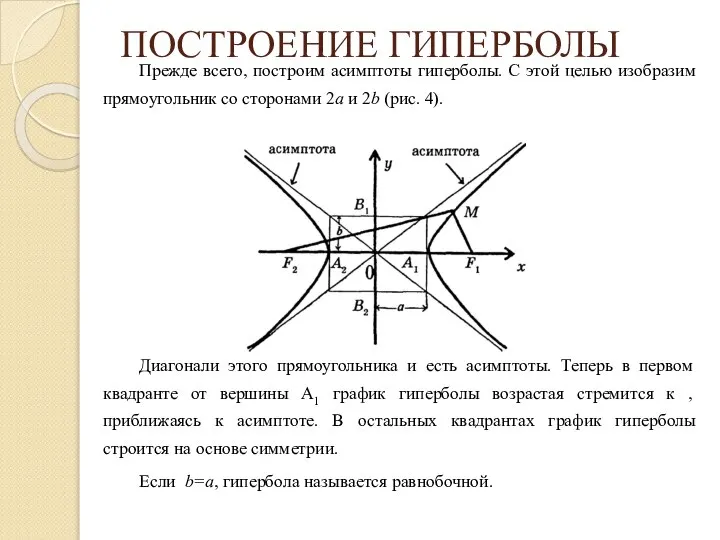
- 34. ПОСТРОЕНИЕ ГИПЕРБОЛЫ Прежде всего, построим асимптоты гиперболы. С этой целью изобразим прямоугольник со сторонами 2а и
- 35. Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине действительной оси: Т. к. с > а, то
- 36. 2.3. ПАРАБОЛА. ВЫВОД УРАВНЕНИЯ Для составления уравнения параболы выбираем систему координат: ось абсцисс проводим через фокус
- 37. Пусть М(х; у) ‒текущая точка параболы, ‒ ее фокус, ‒ основание перпендикуляра, опущенного из точки М
- 39. Скачать презентацию


































 Системи лінійних алгебраїчних рівнянь
Системи лінійних алгебраїчних рівнянь Тестовые задания для ЕНТ - 2017
Тестовые задания для ЕНТ - 2017 Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности ОГЭ по математике – 2018 год
ОГЭ по математике – 2018 год Множества. Операции над множествами
Множества. Операции над множествами Повторяем дроби
Повторяем дроби Математический бой. Внеклассное мероприятие по математике
Математический бой. Внеклассное мероприятие по математике Дифференциальные уравнения 2-го порядка Лекция 5
Дифференциальные уравнения 2-го порядка Лекция 5 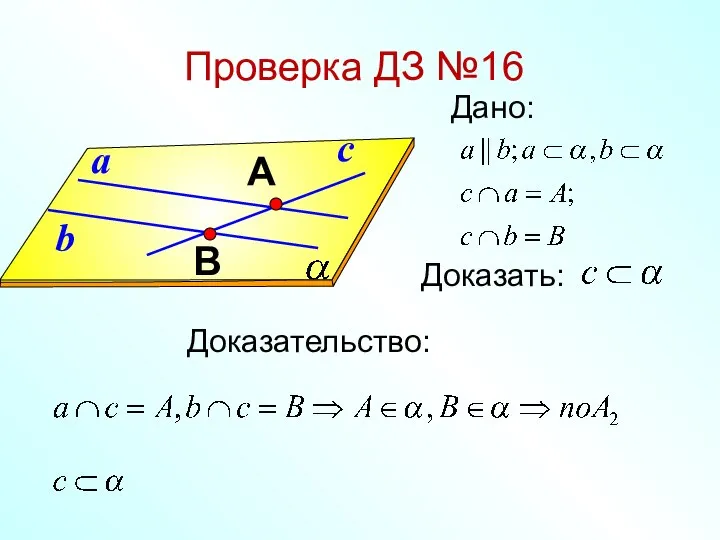 Параллельность прямой и плоскости
Параллельность прямой и плоскости Координатная плоскость
Координатная плоскость Алгебраические методы решения геометрических задач
Алгебраические методы решения геометрических задач Аксиома параллельных прямых
Аксиома параллельных прямых Пирамида. Определение, элементы, площадь поверхност и и объем пирамиды
Пирамида. Определение, элементы, площадь поверхност и и объем пирамиды Пираты Карибского моря. Математика
Пираты Карибского моря. Математика Комплексные числа
Комплексные числа Порядок выполнения действий
Порядок выполнения действий Теорема умножения вероятностей. Решение задач В-10
Теорема умножения вероятностей. Решение задач В-10 Презентация по математике "Построение прямоугольника на нелинованной бумаге" - скачать
Презентация по математике "Построение прямоугольника на нелинованной бумаге" - скачать  Геометрические тела
Геометрические тела Аттестационная работа. Создание творческого проекта «Задачи на движение»
Аттестационная работа. Создание творческого проекта «Задачи на движение» Элементы векторной алгебры (лекция № 2)
Элементы векторной алгебры (лекция № 2) Анализ таблиц сопряжения. Меры эффекта в исследованиях (отношение рисков, шансов)
Анализ таблиц сопряжения. Меры эффекта в исследованиях (отношение рисков, шансов) Закрепление МКОУ «Петуховская средняя школа № 1» Составитель: А.А.Глухова, учитель начальных классов.
Закрепление МКОУ «Петуховская средняя школа № 1» Составитель: А.А.Глухова, учитель начальных классов.  Математическая сказка «Гуси-лебеди»
Математическая сказка «Гуси-лебеди» Смежные углы
Смежные углы Алгебра и начала анализа. Логарифмическая функция Волков С.А. Урюмская средняя школа Тетюшский район Республика Татарстан
Алгебра и начала анализа. Логарифмическая функция Волков С.А. Урюмская средняя школа Тетюшский район Республика Татарстан Правильные многогранники
Правильные многогранники Методы многопарметрической оптимизации
Методы многопарметрической оптимизации